Parsimony and likelihood are two fundamental methods used in phylogenetics to infer evolutionary relationships among species. Parsimony focuses on finding the tree with the minimum number of evolutionary changes, while likelihood evaluates the probability of the observed data given a specific tree and model of evolution. Explore the differences between these approaches to better understand their applications and strengths in evolutionary biology.
Main Difference
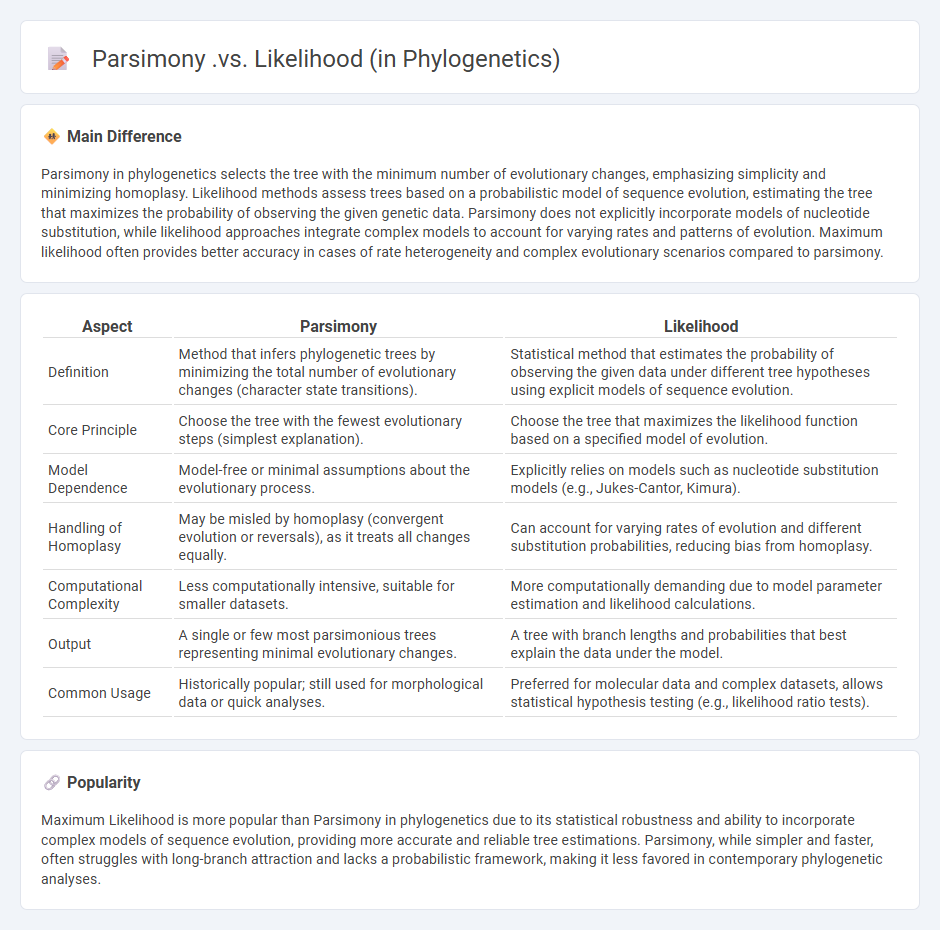
Parsimony in phylogenetics selects the tree with the minimum number of evolutionary changes, emphasizing simplicity and minimizing homoplasy. Likelihood methods assess trees based on a probabilistic model of sequence evolution, estimating the tree that maximizes the probability of observing the given genetic data. Parsimony does not explicitly incorporate models of nucleotide substitution, while likelihood approaches integrate complex models to account for varying rates and patterns of evolution. Maximum likelihood often provides better accuracy in cases of rate heterogeneity and complex evolutionary scenarios compared to parsimony.
Connection
Parsimony and likelihood in phylogenetics are connected through their shared goal of inferring evolutionary trees based on genetic data. Parsimony seeks the tree that minimizes the number of evolutionary changes, while likelihood evaluates the probability of the observed data given a particular tree and model of evolution. Both approaches utilize character state data and evolutionary assumptions to reconstruct phylogenies but differ in their statistical frameworks and computational complexity.
Comparison Table
| Aspect | Parsimony | Likelihood |
|---|---|---|
| Definition | Method that infers phylogenetic trees by minimizing the total number of evolutionary changes (character state transitions). | Statistical method that estimates the probability of observing the given data under different tree hypotheses using explicit models of sequence evolution. |
| Core Principle | Choose the tree with the fewest evolutionary steps (simplest explanation). | Choose the tree that maximizes the likelihood function based on a specified model of evolution. |
| Model Dependence | Model-free or minimal assumptions about the evolutionary process. | Explicitly relies on models such as nucleotide substitution models (e.g., Jukes-Cantor, Kimura). |
| Handling of Homoplasy | May be misled by homoplasy (convergent evolution or reversals), as it treats all changes equally. | Can account for varying rates of evolution and different substitution probabilities, reducing bias from homoplasy. |
| Computational Complexity | Less computationally intensive, suitable for smaller datasets. | More computationally demanding due to model parameter estimation and likelihood calculations. |
| Output | A single or few most parsimonious trees representing minimal evolutionary changes. | A tree with branch lengths and probabilities that best explain the data under the model. |
| Common Usage | Historically popular; still used for morphological data or quick analyses. | Preferred for molecular data and complex datasets, allows statistical hypothesis testing (e.g., likelihood ratio tests). |
Homoplasy
Homoplasy refers to the presence of traits in different species that have arisen independently, rather than from a common ancestor, often due to convergent or parallel evolution. It complicates phylogenetic analysis by obscuring true evolutionary relationships through traits that appear similar but do not indicate shared ancestry. Examples include the wings of bats and birds, which evolved separately to serve the function of flight. Identifying homoplasy requires careful comparison of genetic, morphological, and developmental data.
Model-based inference
Model-based inference in biology leverages computational models and statistical methods to analyze complex biological systems and predict outcomes. Techniques such as Bayesian inference and machine learning are applied to genomic data, ecological models, and systems biology to enhance understanding of biological processes. Recent advancements include integrating multi-omics data sets to refine predictive accuracy and uncover gene-environment interactions. This approach facilitates hypothesis testing and informs experimental design by simulating biological scenarios with higher precision.
Tree topology
Tree topology in biology refers to the branching structure of phylogenetic trees that represent evolutionary relationships among species or genes. These trees illustrate common ancestry and divergence by organizing taxa based on shared characteristics and genetic data. Algorithms like Neighbor-Joining, Maximum Parsimony, and Bayesian Inference optimize tree topology to accurately reconstruct evolutionary history. Accurate tree topology aids in understanding speciation, genetic inheritance, and molecular evolution across organisms.
Character evolution
Character evolution in biology refers to the process by which specific traits or features of organisms change over successive generations through genetic variation and natural selection. These evolutionary changes can involve morphological, physiological, or behavioral characteristics that enhance survival and reproduction in varying environments. Molecular studies of DNA sequences provide crucial insights into the patterns and rates of character evolution across different taxa. Fossil records combined with phylogenetic analyses illuminate the historical progression and diversification of characters over millions of years.
Statistical consistency
Statistical consistency in biology refers to the property of an estimator or method to converge to the true biological parameter as sample size increases. This concept is crucial in evolutionary biology, where consistent phylogenetic inference methods reliably reconstruct species trees from genetic data. For example, maximum likelihood and Bayesian approaches often demonstrate statistical consistency under correct model assumptions. Ensuring consistency allows biologists to make accurate predictions about population genetics, species distributions, and evolutionary relationships from experimental data.
Source and External Links
The Contest Between Parsimony and Likelihood - Maximum parsimony seeks the tree requiring the fewest evolutionary changes to explain observed data, while maximum likelihood finds the tree that makes the observed data most probable given a specified evolutionary model.
Parsimony, Likelihood, and the Role of Models in Molecular Phylogenetics - Maximum parsimony, sometimes justified by minimalism or Ockham's razor, can be used with or without an evolutionary model, whereas maximum likelihood always requires and is defined by an explicit model of evolution.
Parsimony and Maximum-Likelihood Phylogenetic Analyses - Both parsimony and maximum likelihood typically report uncertainty via bootstrapping, which is not intrinsic to either method and differs fundamentally from the probabilistic uncertainty integrated in Bayesian methods.
FAQs
What is phylogenetic analysis?
Phylogenetic analysis is the study of evolutionary relationships among species or genes using genetic, morphological, or molecular data to construct a phylogenetic tree.
What is the parsimony principle in phylogenetics?
The parsimony principle in phylogenetics states that the preferred evolutionary tree is the one that requires the smallest number of genetic changes or evolutionary events.
What is likelihood in phylogenetic inference?
Likelihood in phylogenetic inference is the probability of observing the given genetic data under a specific evolutionary tree and model.
How do parsimony and likelihood methods differ?
Parsimony methods infer phylogenetic trees by minimizing the total number of evolutionary changes, while likelihood methods estimate trees based on the probability of observing the given data under a specific evolutionary model.
What are the advantages of using parsimony?
Parsimony minimizes model complexity, enhances interpretability, reduces overfitting, and improves computational efficiency.
What are the strengths of likelihood methods?
Likelihood methods provide consistent parameter estimates, enable efficient use of data, allow hypothesis testing through likelihood ratio tests, and support model comparison using metrics like AIC or BIC.
In which cases would one method be preferred over the other?
Method A is preferred for large datasets requiring quick processing, while Method B excels in accuracy and handling complex data patterns.
 calledges.com
calledges.com