Type I error occurs when a true null hypothesis is incorrectly rejected, resulting in a false positive. Type II error happens when a false null hypothesis is not rejected, leading to a false negative. Explore more to understand their impact on statistical hypothesis testing.
Main Difference
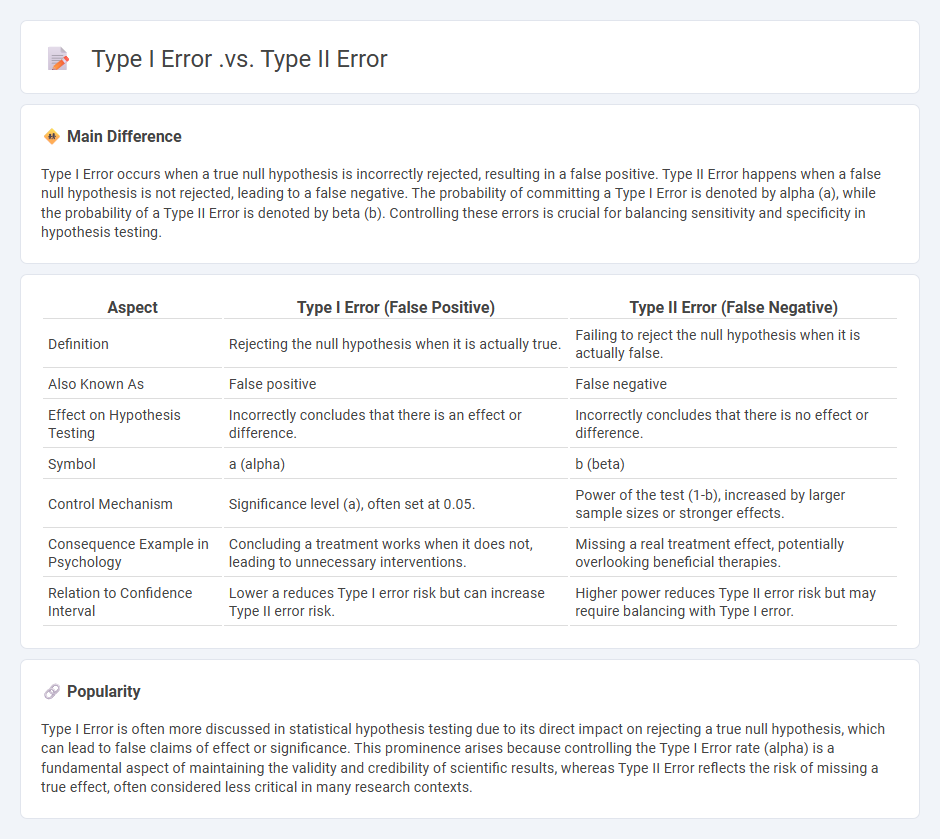
Type I Error occurs when a true null hypothesis is incorrectly rejected, resulting in a false positive. Type II Error happens when a false null hypothesis is not rejected, leading to a false negative. The probability of committing a Type I Error is denoted by alpha (a), while the probability of a Type II Error is denoted by beta (b). Controlling these errors is crucial for balancing sensitivity and specificity in hypothesis testing.
Connection
Type I error occurs when a true null hypothesis is incorrectly rejected, representing a false positive, while Type II error happens when a false null hypothesis is not rejected, indicating a false negative. The probabilities of Type I error (alpha) and Type II error (beta) are inversely related and depend on the chosen significance level, sample size, and effect size. Balancing these errors is crucial in hypothesis testing to optimize test power and minimize incorrect conclusions.
Comparison Table
| Aspect | Type I Error (False Positive) | Type II Error (False Negative) |
|---|---|---|
| Definition | Rejecting the null hypothesis when it is actually true. | Failing to reject the null hypothesis when it is actually false. |
| Also Known As | False positive | False negative |
| Effect on Hypothesis Testing | Incorrectly concludes that there is an effect or difference. | Incorrectly concludes that there is no effect or difference. |
| Symbol | a (alpha) | b (beta) |
| Control Mechanism | Significance level (a), often set at 0.05. | Power of the test (1-b), increased by larger sample sizes or stronger effects. |
| Consequence Example in Psychology | Concluding a treatment works when it does not, leading to unnecessary interventions. | Missing a real treatment effect, potentially overlooking beneficial therapies. |
| Relation to Confidence Interval | Lower a reduces Type I error risk but can increase Type II error risk. | Higher power reduces Type II error risk but may require balancing with Type I error. |
False Positive
False positive in psychology refers to the incorrect identification of a stimulus or condition as present when it is actually absent. This phenomenon often occurs in diagnostic testing, where a test mistakenly indicates the presence of a mental disorder despite its absence. Cognitive biases and errors in perception can also contribute to false positives in psychological assessments. Understanding false positives is crucial for improving diagnostic accuracy and reducing misdiagnosis in clinical settings.
False Negative
A false negative in psychology occurs when a diagnostic test or assessment fails to detect a condition that is actually present, leading to an incorrect conclusion that an individual does not have the disorder or issue. This error can affect clinical decision-making, delaying appropriate treatment for mental health conditions such as depression, anxiety, or schizophrenia. False negatives are particularly problematic in psychological testing like the Beck Depression Inventory or PTSD screening, where sensitivity and specificity rates critically influence diagnosis accuracy. Minimizing false negatives involves refining assessment tools and integrating multiple diagnostic methods to ensure thorough mental health evaluations.
Significance Level (Alpha)
The significance level (alpha) in psychology represents the threshold probability for rejecting the null hypothesis, typically set at 0.05 or 5%. It quantifies the risk of committing a Type I error, which occurs when a true null hypothesis is incorrectly rejected. Researchers use the alpha level to determine the statistical significance of experimental results, ensuring findings are not due to random chance. Common statistical tests like t-tests and ANOVA rely on alpha to evaluate hypotheses in psychological research.
Statistical Power (1-Beta)
Statistical power (1-b) in psychology measures the probability of correctly rejecting a false null hypothesis, typically aiming for at least 0.80 to reduce Type II errors. Factors influencing power include sample size, effect size, significance level (a), and variability within data. Increasing sample size or effect size enhances power, enabling more reliable detection of psychological phenomena such as treatment effects or cognitive differences. Power analysis guides study design to balance resource use and the potential for meaningful, replicable psychological findings.
Hypothesis Testing
Hypothesis testing in psychology is a statistical method used to determine the validity of a research hypothesis by analyzing experimental or observational data. Psychologists formulate null and alternative hypotheses to evaluate cognitive, behavioral, or emotional phenomena through controlled experiments or surveys. Statistical tests such as t-tests, ANOVA, and chi-square tests help assess the probability that observed effects occurred by chance, typically using a significance level (alpha) of 0.05. This process is fundamental for validating theories and advancing psychological science by providing empirical evidence.
Source and External Links
Type I and type II errors - Wikipedia - Type I error is a false positive, rejecting a true null hypothesis, while Type II error is a false negative, failing to reject a false null hypothesis, with applications in many scientific fields.
Type I & Type II Errors | Differences, Examples, Visualizations - Scribbr - Type I error is falsely concluding an effect exists (false positive), and Type II error is failing to detect an effect that exists (false negative), with a trade-off between their probabilities depending on significance level and test power.
What are Type 1 and Type 2 Errors in Statistics? - Simply Psychology - Type I error is rejecting a true null hypothesis (false positive) and Type II error is not rejecting a false null hypothesis (false negative), and their probabilities inversely vary with the significance level (alpha).
FAQs
What is a statistical error?
A statistical error is the difference between an observed value and the true population parameter, typically caused by sampling variability or measurement inaccuracies.
What is a Type I Error?
A Type I Error occurs when a true null hypothesis is incorrectly rejected in statistical hypothesis testing.
What is a Type II Error?
A Type II Error occurs when a statistical test fails to reject a false null hypothesis, resulting in a false negative.
How do Type I and Type II Errors differ?
Type I Error refers to rejecting a true null hypothesis (false positive), while Type II Error refers to failing to reject a false null hypothesis (false negative).
What causes a Type I Error?
A Type I Error is caused by rejecting a true null hypothesis due to random sampling variability or an overly strict significance level (alpha).
What causes a Type II Error?
A Type II Error is caused by insufficient statistical power, small sample size, high variability, or an effect size that is too small to detect, leading to the failure to reject a false null hypothesis.
How can researchers reduce statistical errors?
Researchers can reduce statistical errors by increasing sample size, using precise measurement tools, applying appropriate statistical tests, controlling confounding variables, and ensuring proper study design and data collection methods.
 calledges.com
calledges.com