Turing completeness defines a system's ability to perform any computation given enough time and memory, exemplified by modern programming languages and universal machines. Non-Turing complete systems, such as regular expressions and finite automata, are limited by their inability to simulate arbitrary algorithms and handle infinite loops. Explore the distinctions and implications of these computational models to deepen your understanding.
Main Difference
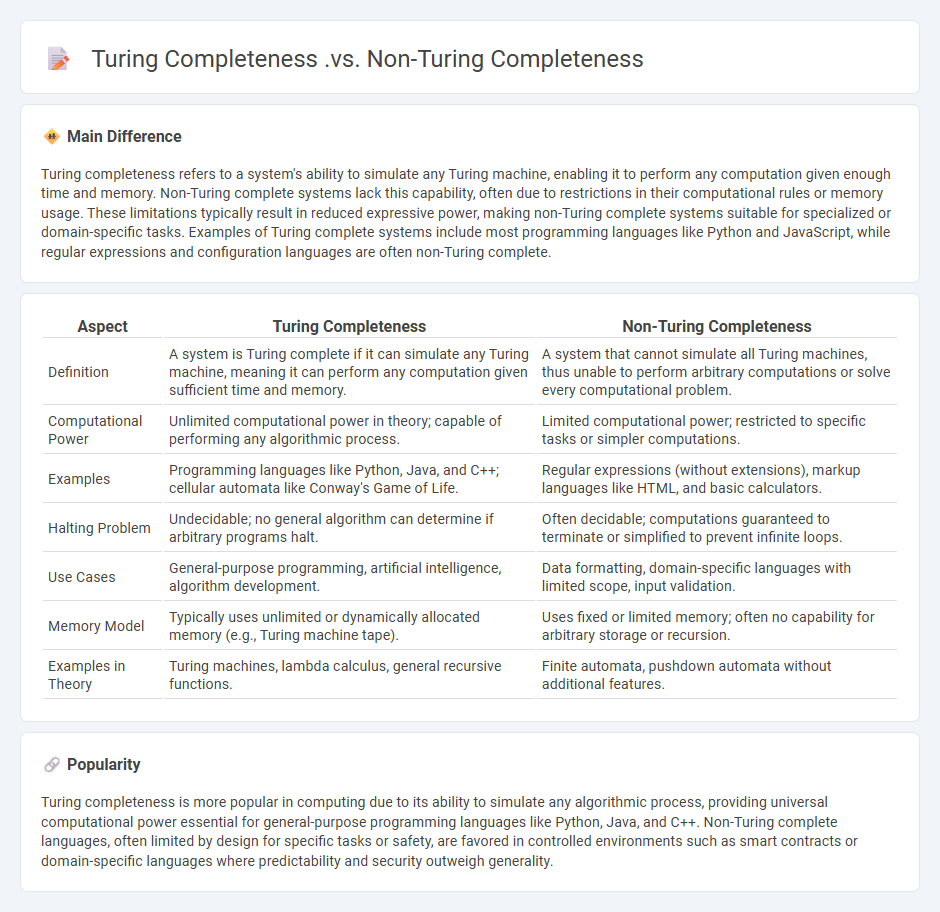
Turing completeness refers to a system's ability to simulate any Turing machine, enabling it to perform any computation given enough time and memory. Non-Turing complete systems lack this capability, often due to restrictions in their computational rules or memory usage. These limitations typically result in reduced expressive power, making non-Turing complete systems suitable for specialized or domain-specific tasks. Examples of Turing complete systems include most programming languages like Python and JavaScript, while regular expressions and configuration languages are often non-Turing complete.
Connection
Turing completeness defines computational systems capable of simulating any Turing machine, enabling them to perform any algorithmic task given sufficient resources. Non-Turing complete systems have restricted computational abilities, often designed for specific, limited purposes to ensure decidability and avoid infinite loops. The relationship between them highlights trade-offs in expressiveness versus guaranteed termination, crucial for programming language theory and formal verification.
Comparison Table
| Aspect | Turing Completeness | Non-Turing Completeness |
|---|---|---|
| Definition | A system is Turing complete if it can simulate any Turing machine, meaning it can perform any computation given sufficient time and memory. | A system that cannot simulate all Turing machines, thus unable to perform arbitrary computations or solve every computational problem. |
| Computational Power | Unlimited computational power in theory; capable of performing any algorithmic process. | Limited computational power; restricted to specific tasks or simpler computations. |
| Examples | Programming languages like Python, Java, and C++; cellular automata like Conway's Game of Life. | Regular expressions (without extensions), markup languages like HTML, and basic calculators. |
| Halting Problem | Undecidable; no general algorithm can determine if arbitrary programs halt. | Often decidable; computations guaranteed to terminate or simplified to prevent infinite loops. |
| Use Cases | General-purpose programming, artificial intelligence, algorithm development. | Data formatting, domain-specific languages with limited scope, input validation. |
| Memory Model | Typically uses unlimited or dynamically allocated memory (e.g., Turing machine tape). | Uses fixed or limited memory; often no capability for arbitrary storage or recursion. |
| Examples in Theory | Turing machines, lambda calculus, general recursive functions. | Finite automata, pushdown automata without additional features. |
Computational Universality
Computational universality refers to the capability of a computational system, such as a Turing machine or modern computer, to simulate any other computational system given appropriate resources like time and memory. This concept underpins the theory of computation, demonstrating that universal machines can perform any algorithmic task that any other machine can. It plays a critical role in computer science, enabling advancements in programming languages, algorithm design, and artificial intelligence. Real-world applications include general-purpose processors and software platforms capable of running diverse programs across various domains.
Halting Problem
The Halting Problem is a fundamental concept in theoretical computer science that addresses whether a given computer program will finish running or continue to execute indefinitely. Alan Turing proved in 1936 that a general algorithm to solve the Halting Problem for all possible program-input pairs cannot exist, establishing the problem as undecidable. This result has profound implications for the limits of computation, influencing the development of computability theory and formal language theory. Modern computer science research continues to explore related undecidability issues and their impact on software verification and automated reasoning.
Expressiveness
Expressiveness in computer science refers to the ability of a programming language or computational system to represent a wide range of computations and algorithms efficiently. It measures how easily and succinctly a language can describe complex ideas, control structures, and data manipulations. Highly expressive languages like Python and Haskell enable developers to write concise code that enhances readability and maintainability. Expressiveness directly impacts software development productivity and the ease of implementing diverse computational tasks.
Decidability
Decidability in computer science refers to the ability to determine, through an algorithm, whether a given problem can be solved with a yes or no answer. It plays a crucial role in the theory of computation, particularly in classifying problems as decidable or undecidable. The Halting Problem is a classic example of an undecidable problem, demonstrating limits of algorithmic computation. Understanding decidability helps optimize problem-solving approaches and influences computational complexity analysis.
Language Restrictions
Language restrictions in computer systems refer to limitations imposed on programming or scripting languages, affecting their syntax, semantics, or operational scope. These restrictions influence software development by constraining code portability, affecting compatibility between different platforms, and potentially reducing the effectiveness of language features like dynamic typing or multithreading. Understanding language restrictions is essential for developers working with domain-specific languages, embedded systems, or secure coding environments to ensure compliance and maintain system integrity. Examples include Java's restriction on pointer arithmetic and Python's Global Interpreter Lock (GIL) which limits native multithreading performance.
Source and External Links
Exploring Turing Completeness | Lenovo US - Turing complete means a system can simulate any computational device, allowing it to perform any computation, while non-Turing complete systems are limited to specific tasks, often designed for safety or efficiency in certain domains.
What is Turing complete? - Bitstamp - Turing completeness means a programming system can solve any computational problem given enough time and resources, exemplified by Ethereum's Solidity language, whereas Bitcoin uses a non-Turing complete scripting language limited to transaction processing.
It doesn't have to be Turing complete to be useful - Increment - Turing incomplete (non-Turing complete) languages restrict computability by omitting operations vital for universal computation, which offers advantages in safety and domain-specific applications despite their limited computational scope.
FAQs
What does it mean to be Turing complete?
Turing complete means a system can perform any computation that a Turing machine can, given sufficient time and memory.
What is a non-Turing complete system?
A non-Turing complete system is a computational model or language that lacks the full computational power of a Turing machine, meaning it cannot perform all possible algorithms or simulate arbitrary computations.
How do Turing complete and non-Turing complete languages differ?
Turing complete languages can simulate any Turing machine, allowing them to express all computable functions, while non-Turing complete languages have restricted computational power and cannot perform arbitrary computation.
What are examples of Turing complete systems?
Examples of Turing complete systems include programming languages like Python, Java, and C++; computational models such as Turing machines and lambda calculus; and platforms like the Ethereum blockchain's smart contract language Solidity.
What are examples of non-Turing complete systems?
Examples of non-Turing complete systems include regular expressions (without backreferences), finite automata, context-free grammars, and certain domain-specific languages like SQL query languages and spreadsheet formulas.
Why does Turing completeness matter in programming?
Turing completeness matters in programming because it ensures a language or system can simulate any computation, enabling the creation of versatile, powerful, and universal software solutions.
Can a non-Turing complete language solve all computational problems?
A non-Turing complete language cannot solve all computational problems because it lacks the computational expressiveness needed to simulate any Turing machine.
 calledges.com
calledges.com