Turing completeness refers to a system's ability to simulate any Turing machine, meaning it can perform any computation given enough time and resources. Turing decidability, on the other hand, concerns whether a problem can be resolved algorithmically within finite time by a Turing machine. Explore deeper insights into the foundational concepts of computability theory and their implications.
Main Difference
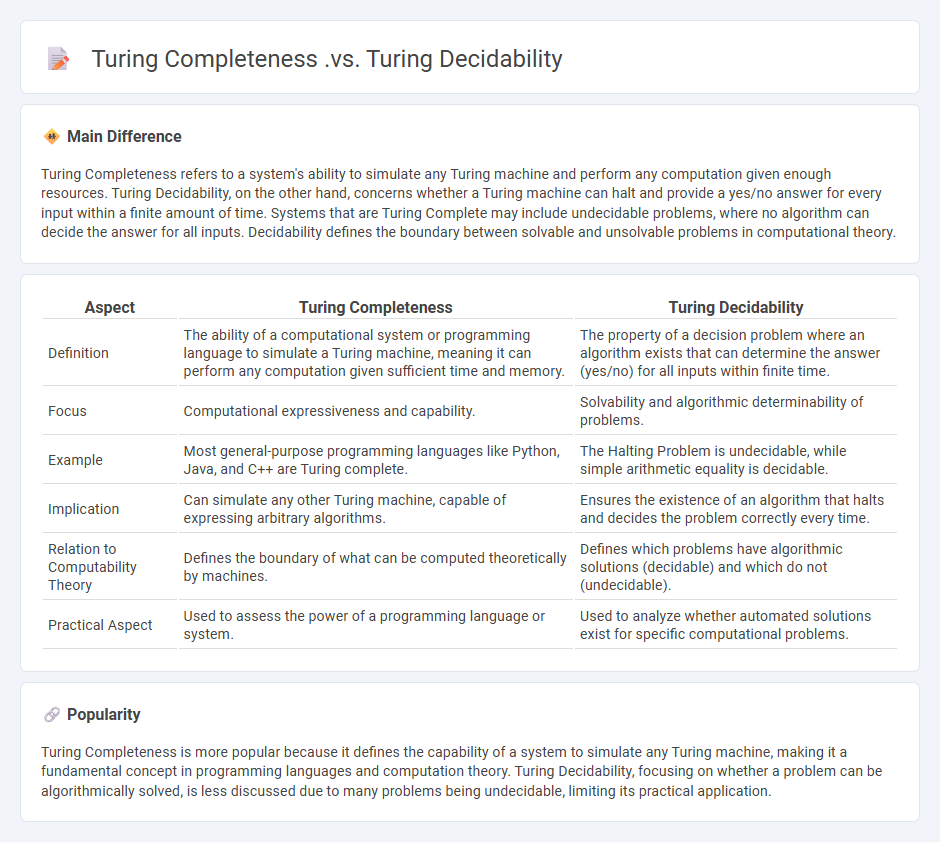
Turing Completeness refers to a system's ability to simulate any Turing machine and perform any computation given enough resources. Turing Decidability, on the other hand, concerns whether a Turing machine can halt and provide a yes/no answer for every input within a finite amount of time. Systems that are Turing Complete may include undecidable problems, where no algorithm can decide the answer for all inputs. Decidability defines the boundary between solvable and unsolvable problems in computational theory.
Connection
Turing completeness refers to a system's ability to simulate any Turing machine, enabling it to perform any computation given enough time and memory. Turing decidability, on the other hand, determines whether a problem can be algorithmically decided or solved by a Turing machine in a finite amount of time. The connection lies in that while Turing-complete systems can simulate all computations, they also encompass problems that are undecidable, highlighting the limits of algorithmic solvability within such systems.
Comparison Table
| Aspect | Turing Completeness | Turing Decidability |
|---|---|---|
| Definition | The ability of a computational system or programming language to simulate a Turing machine, meaning it can perform any computation given sufficient time and memory. | The property of a decision problem where an algorithm exists that can determine the answer (yes/no) for all inputs within finite time. |
| Focus | Computational expressiveness and capability. | Solvability and algorithmic determinability of problems. |
| Example | Most general-purpose programming languages like Python, Java, and C++ are Turing complete. | The Halting Problem is undecidable, while simple arithmetic equality is decidable. |
| Implication | Can simulate any other Turing machine, capable of expressing arbitrary algorithms. | Ensures the existence of an algorithm that halts and decides the problem correctly every time. |
| Relation to Computability Theory | Defines the boundary of what can be computed theoretically by machines. | Defines which problems have algorithmic solutions (decidable) and which do not (undecidable). |
| Practical Aspect | Used to assess the power of a programming language or system. | Used to analyze whether automated solutions exist for specific computational problems. |
Computation Limits
Computation limits in computer science refer to the theoretical boundaries on what problems can be solved using algorithms within finite time and resources. These limits are characterized by complexity classes such as P, NP, and PSPACE, defining the computational effort required. Understanding computation limits is crucial for optimizing algorithms and identifying tasks that are inherently unsolvable or intractable. Advances in quantum computing challenge traditional computation boundaries by potentially solving specific problems more efficiently than classical computers.
Halting Problem
The Halting Problem, a fundamental concept in computer science, concerns determining whether a given computer program will finish running or continue indefinitely. Alan Turing proved in 1936 that a general algorithm to solve the Halting Problem for all possible program-input pairs cannot exist. This undecidability result is central to computability theory and influences software verification, compiler design, and the limits of automated reasoning. Modern applications often rely on approximations or restricted versions of halting analysis to ensure program correctness.
Expressive Power
Expressive power in computer science refers to the ability of a programming language or computational model to represent a wide variety of algorithms and data structures efficiently. Languages with high expressive power enable developers to write concise, readable code that can solve complex problems while abstracting underlying hardware details. Models like Turing machines are considered maximally expressive because they can simulate any algorithmic process. The balance between expressive power and computational efficiency is critical for effective software design and implementation.
Decidable Languages
Decidable languages are a class of formal languages for which there exists a Turing machine that accepts every string in the language and halts on all inputs. These languages are also known as recursive languages and are fundamental in computability theory. Examples include regular languages, context-free languages, and any language decided by a deterministic Turing machine within finite time. Decidable languages contrast with undecidable ones, where no algorithm can uniformly decide membership for all inputs.
Recursively Enumerable
Recursively enumerable languages are a fundamental concept in the theory of computation and formal language theory. They are defined by Turing machines that accept strings belonging to the language but may run indefinitely for strings not in the language. These languages encompass all languages for which membership can be semi-decided by a Turing machine, meaning the machine halts and accepts if the string is in the language but may never halt if it is not. Recursively enumerable sets are also known as Turing-recognizable languages and represent the broadest class of languages decidable by algorithmic processes without guarantees of termination on rejection.
Source and External Links
Decidability - Stacks Documentation - Turing completeness is a property of computational systems that can simulate any Turing machine, while decidability is a property of problems where an algorithm always halts with an answer; non-Turing complete languages are decidable but have limited computational power compared to Turing-complete ones.
Turing completeness - Wikipedia - Turing completeness means a system or language can simulate any Turing machine, thus capable of expressing any computable function, whereas decidability refers to whether a problem can be algorithmically decided by halting for all inputs.
There are no useful programs that require Turing completeness ... - Hacker News - Decidable languages are less powerful than Turing-complete languages; Turing completeness allows for programs with potentially infinite loops and undecidable behaviors, while decidability ensures guaranteed termination but restricts expressive power.
FAQs
What is Turing completeness?
Turing completeness is the capability of a system or programming language to simulate any Turing machine, enabling it to perform any computable function given sufficient time and memory.
What does Turing decidability mean?
Turing decidability means a problem can be solved by a Turing machine that halts and gives a correct yes or no answer for every input instance.
How is Turing completeness different from Turing decidability?
Turing completeness refers to a system's ability to simulate any Turing machine and perform any computation given enough time and memory, while Turing decidability indicates whether a problem can be algorithmically decided (halted with a yes/no answer) by a Turing machine.
Can a Turing-complete system solve undecidable problems?
A Turing-complete system cannot solve undecidable problems, such as the Halting Problem, due to fundamental computational limits proven by Alan Turing.
What are examples of Turing-complete and non-Turing-complete systems?
Examples of Turing-complete systems include Python, JavaScript, and the Lambda calculus; non-Turing-complete systems include regular expressions, SQL (without recursion), and HTML.
Why are some problems undecidable for Turing machines?
Some problems are undecidable for Turing machines because they require solving the Halting Problem or equivalent tasks, where no algorithm can determine in all cases whether a machine halts or runs indefinitely.
How does Turing completeness impact programming language design?
Turing completeness ensures a programming language can express any computation given sufficient resources, influencing language designers to balance expressive power with usability, performance, and safety features.
 calledges.com
calledges.com