Deductive reasoning starts with general premises and moves to a specific conclusion, ensuring certainty if the premises are true. Inductive reasoning involves drawing general conclusions from specific observations, offering probable but not guaranteed outcomes. Explore the distinctions to deepen your understanding of philosophical logic.
Main Difference
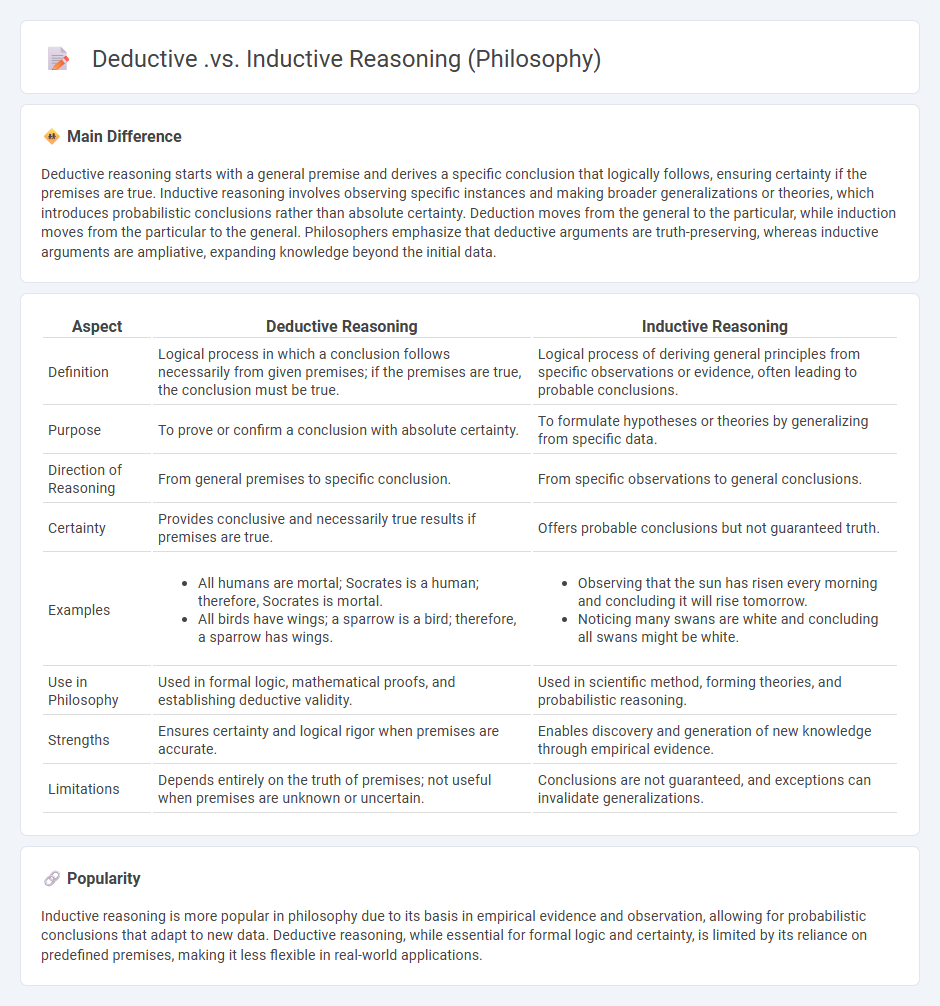
Deductive reasoning starts with a general premise and derives a specific conclusion that logically follows, ensuring certainty if the premises are true. Inductive reasoning involves observing specific instances and making broader generalizations or theories, which introduces probabilistic conclusions rather than absolute certainty. Deduction moves from the general to the particular, while induction moves from the particular to the general. Philosophers emphasize that deductive arguments are truth-preserving, whereas inductive arguments are ampliative, expanding knowledge beyond the initial data.
Connection
Deductive reasoning in philosophy involves deriving specific conclusions from general premises, ensuring logical certainty when the premises are true, while inductive reasoning infers general principles from specific observations, providing probabilistic support. Both methods are interconnected as they complement each other in the process of knowledge acquisition: deduction tests hypotheses generated through induction. Philosophers analyze this interplay to understand justification, evidential support, and the development of scientific theories.
Comparison Table
| Aspect | Deductive Reasoning | Inductive Reasoning |
|---|---|---|
| Definition | Logical process in which a conclusion follows necessarily from given premises; if the premises are true, the conclusion must be true. | Logical process of deriving general principles from specific observations or evidence, often leading to probable conclusions. |
| Purpose | To prove or confirm a conclusion with absolute certainty. | To formulate hypotheses or theories by generalizing from specific data. |
| Direction of Reasoning | From general premises to specific conclusion. | From specific observations to general conclusions. |
| Certainty | Provides conclusive and necessarily true results if premises are true. | Offers probable conclusions but not guaranteed truth. |
| Examples |
|
|
| Use in Philosophy | Used in formal logic, mathematical proofs, and establishing deductive validity. | Used in scientific method, forming theories, and probabilistic reasoning. |
| Strengths | Ensures certainty and logical rigor when premises are accurate. | Enables discovery and generation of new knowledge through empirical evidence. |
| Limitations | Depends entirely on the truth of premises; not useful when premises are unknown or uncertain. | Conclusions are not guaranteed, and exceptions can invalidate generalizations. |
Generalization
Generalization is a cognitive process where specific observations are broadened to form general principles or rules. It enables the application of learned concepts to new situations by identifying common patterns or attributes. In English linguistics, generalization often refers to extending word meanings beyond their original contexts, such as the semantic broadening of terms. This process aids in language acquisition and adaptive communication by allowing flexibility in interpretation and usage.
Specificity
Specificity in English refers to the accuracy and precision with which language conveys meaning, ensuring clarity in communication. It involves using detailed and exact words to describe objects, actions, or concepts, reducing ambiguity for the reader or listener. Linguistic specificity enhances understanding in fields like legal documents, scientific writing, and technical manuals where precise information is critical. High specificity in English contributes to effective information exchange and minimizes misinterpretation.
Logical certainty
Logical certainty represents a level of confidence where a proposition or statement is unequivocally true based on formal logic and deductive reasoning. It relies on valid premises and inference rules within mathematical logic, ensuring conclusions are irrefutable if the initial assumptions hold. Classical logic frameworks, such as propositional and predicate logic, provide the foundation for establishing logical certainty in various disciplines including computer science, philosophy, and mathematics. This principle is essential for creating reliable algorithms, proofs, and decision-making systems.
Probability
Probability quantifies the likelihood of an event occurring, expressed as a number between 0 and 1, where 0 indicates impossibility and 1 signifies certainty. It is calculated by dividing the favorable outcomes by the total possible outcomes in a well-defined sample space. Probability theory underpins fields such as statistics, finance, machine learning, and risk assessment, providing foundational tools for decision-making under uncertainty. Classical examples include coin tosses, dice rolls, and real-world applications like weather forecasting and insurance modeling.
Premises
Premises refer to physical locations or properties owned, leased, or used by a business or individual for operational purposes. These can include office buildings, warehouses, retail spaces, or manufacturing facilities, typically identified by a specific address. Proper maintenance and security of premises ensure safety compliance with regulations such as OSHA in the United States. Real estate valuation of premises involves factors like location, size, infrastructure quality, and market demand.
Source and External Links
Deductive and Inductive Arguments - Deductive arguments guarantee the truth of the conclusion if the premises are true, while inductive arguments only make the conclusion probable based on the premises.
The difference between inductive and deductive reasoning - Inductive reasoning moves from specific observations to general theories, whereas deductive reasoning applies general principles to reach specific conclusions.
Inductive vs. Deductive Research Approach | Steps & Examples - Inductive reasoning develops new theories from observations, while deductive reasoning tests existing theories by deriving specific predictions from general statements.
FAQs
What is deductive reasoning in philosophy?
Deductive reasoning in philosophy is a logical process where conclusions necessarily follow from given premises, ensuring truth preservation if the premises are true.
What is inductive reasoning in philosophy?
Inductive reasoning in philosophy is a method of reasoning that involves drawing generalized conclusions from specific observations or instances.
How do deductive and inductive reasoning differ?
Deductive reasoning derives specific conclusions from general premises with certainty, while inductive reasoning generates probable generalizations based on specific observations.
What are examples of deductive reasoning?
If all humans are mortal, and Socrates is a human, then Socrates is mortal; all birds have feathers, and a robin is a bird, so a robin has feathers; if it rains, the ground gets wet, it is raining, therefore the ground is wet.
What are examples of inductive reasoning?
Observing that the sun rises every morning and concluding it will rise tomorrow, noticing that all swans seen so far are white and inferring all swans are white, and noting that a coin flipped multiple times lands on heads frequently and predicting it will lands on heads again.
When is deductive reasoning more reliable?
Deductive reasoning is more reliable when the premises are true and the logical structure is valid, ensuring that conclusions are necessarily true.
What are the limitations of inductive reasoning?
Inductive reasoning is limited by the possibility of false generalizations due to insufficient or unrepresentative data and cannot guarantee certainty, only probabilistic conclusions.
 calledges.com
calledges.com