Theoretical mathematics focuses on abstract concepts and foundational principles, exploring mathematical structures and proving theorems without immediate concern for practical applications. Applied mathematics utilizes these theories to solve real-world problems in fields such as engineering, physics, and finance through mathematical modeling and computational techniques. Discover more about the distinct approaches and impacts of theoretical and applied mathematics.
Main Difference
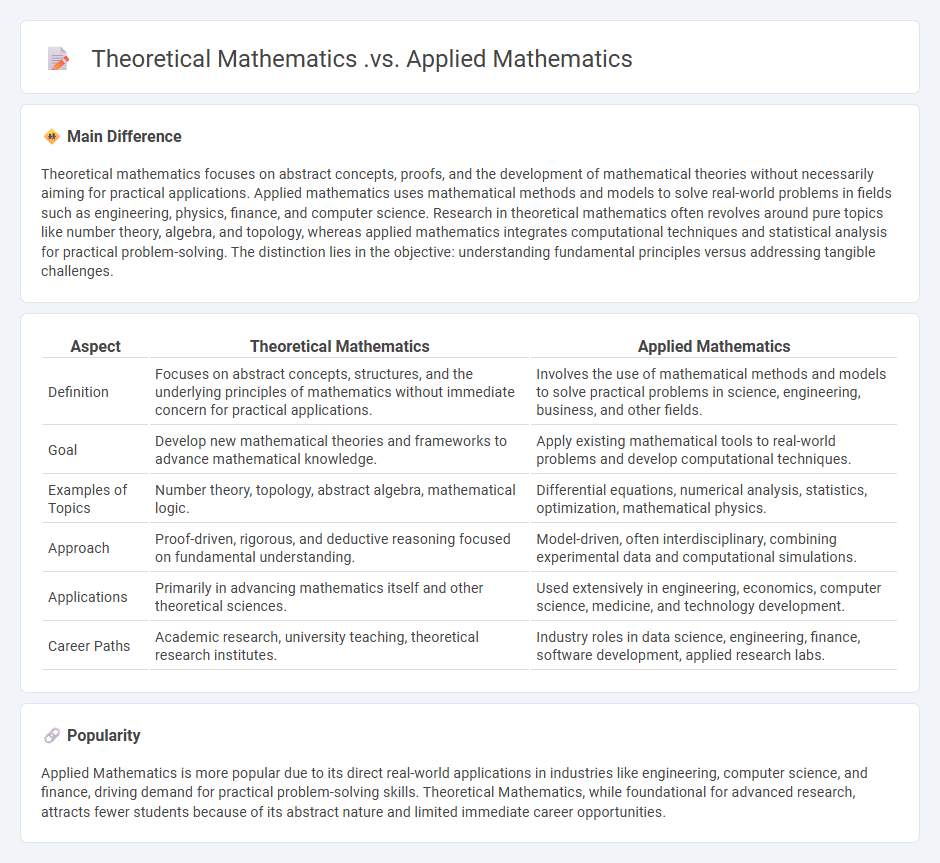
Theoretical mathematics focuses on abstract concepts, proofs, and the development of mathematical theories without necessarily aiming for practical applications. Applied mathematics uses mathematical methods and models to solve real-world problems in fields such as engineering, physics, finance, and computer science. Research in theoretical mathematics often revolves around pure topics like number theory, algebra, and topology, whereas applied mathematics integrates computational techniques and statistical analysis for practical problem-solving. The distinction lies in the objective: understanding fundamental principles versus addressing tangible challenges.
Connection
Theoretical mathematics provides the foundational principles and abstract frameworks that underpin applied mathematics, enabling the formulation of precise models and solutions for real-world problems. Applied mathematics utilizes these theoretical constructs to develop algorithms, simulations, and statistical methods in fields such as engineering, physics, and computer science. This symbiotic relationship ensures continuous advancement and practical innovation across scientific disciplines.
Comparison Table
| Aspect | Theoretical Mathematics | Applied Mathematics |
|---|---|---|
| Definition | Focuses on abstract concepts, structures, and the underlying principles of mathematics without immediate concern for practical applications. | Involves the use of mathematical methods and models to solve practical problems in science, engineering, business, and other fields. |
| Goal | Develop new mathematical theories and frameworks to advance mathematical knowledge. | Apply existing mathematical tools to real-world problems and develop computational techniques. |
| Examples of Topics | Number theory, topology, abstract algebra, mathematical logic. | Differential equations, numerical analysis, statistics, optimization, mathematical physics. |
| Approach | Proof-driven, rigorous, and deductive reasoning focused on fundamental understanding. | Model-driven, often interdisciplinary, combining experimental data and computational simulations. |
| Applications | Primarily in advancing mathematics itself and other theoretical sciences. | Used extensively in engineering, economics, computer science, medicine, and technology development. |
| Career Paths | Academic research, university teaching, theoretical research institutes. | Industry roles in data science, engineering, finance, software development, applied research labs. |
Abstract Concepts
Abstract concepts such as freedom, justice, and love play a crucial role in shaping human cognition and communication. These intangible ideas are often represented through language, art, and symbols, allowing individuals to express complex thoughts and emotions. In cognitive science, abstract concepts are studied to understand how the brain processes non-concrete information, often involving regions like the prefrontal cortex. Understanding abstract concepts enhances artificial intelligence development by improving natural language processing and semantic comprehension.
Real-World Applications
Artificial intelligence powers real-world applications across diverse industries including healthcare, finance, and transportation. Machine learning algorithms enhance medical diagnoses by analyzing imaging data, leading to earlier detection of diseases such as cancer. In finance, AI-driven models optimize trading strategies and detect fraudulent activities with high accuracy. Autonomous vehicles rely on AI sensors and computer vision to navigate complex environments safely and efficiently.
Mathematical Modeling
Mathematical modeling involves creating abstract representations of real-world systems using mathematical language and techniques to analyze behavior and predict outcomes. It incorporates differential equations, statistical models, and computational algorithms to simulate phenomena across physics, biology, economics, and engineering. Key applications include climate forecasting, population dynamics, and financial risk assessment, where models provide critical insights for decision-making. Effective mathematical models undergo validation against empirical data to ensure accuracy and reliability.
Proofs and Theorems
Proofs and theorems form the foundation of mathematical logic and reasoning, providing rigorous validation for mathematical statements. A theorem is a proposition that has been proven based on previously established axioms and lemmas. Proofs can be constructed using various methods such as direct proof, contradiction, induction, and contrapositive, ensuring the reliability and consistency of mathematical systems. Major theorems like Fermat's Last Theorem and the Pythagorean Theorem illustrate the application and significance of formal proofs in advancing mathematical knowledge.
Problem-Solving Methods
Problem-solving methods encompass techniques such as the scientific method, heuristic approaches, trial and error, and algorithmic processes. The scientific method involves hypothesis formulation, experimentation, and observation to reach logical conclusions. Heuristic techniques rely on practical shortcuts and experience-based rules to simplify complex problems. Algorithmic methods use step-by-step procedures or formulas that guarantee solutions when correctly applied.
Source and External Links
Pure Math vs Applied Math - This article explains the differences between pure and applied mathematics, highlighting their focus, coursework, and applications in real-world fields.
Maths vs Applied maths - This video discusses the distinction between pure and applied mathematics, focusing on their theoretical and practical aspects.
Pure vs. Applied Mathematics - This article outlines key differences between pure and applied mathematics, including their focus on abstract concepts versus real-world applications.
FAQs
What is theoretical mathematics?
Theoretical mathematics is a branch of mathematics focused on abstract concepts, structures, and proofs without immediate concern for practical applications.
What is applied mathematics?
Applied mathematics is the branch of mathematics that uses mathematical methods and models to solve practical problems in science, engineering, and industry.
How do theoretical and applied mathematics differ?
Theoretical mathematics focuses on abstract concepts and proving theorems, while applied mathematics uses mathematical methods to solve practical problems in fields like science, engineering, and finance.
What skills are needed for theoretical mathematics?
Theoretical mathematics requires strong abstract reasoning, logical thinking, problem-solving skills, proficiency in mathematical proofs, deep understanding of algebra, analysis, topology, and familiarity with advanced mathematical concepts and structures.
What careers use applied mathematics?
Careers using applied mathematics include data science, engineering, finance, operations research, computer science, physics, actuarial science, and quantitative analysis.
Can theoretical math ideas become practical?
Theoretical math ideas become practical when applied in fields such as cryptography, computer science, physics, and engineering, transforming abstract concepts into real-world technologies and solutions.
Why is applied mathematics important in real life?
Applied mathematics is important in real life because it provides essential tools for solving practical problems in engineering, economics, medicine, physics, and computer science, enhancing decision-making, innovation, and technology development.
 calledges.com
calledges.com