Absolute convergence occurs when the series of absolute values of the terms converges, ensuring the original series converges regardless of term rearrangement. Conditional convergence happens when a series converges only if the terms are in a specific order, but the series of absolute values diverges. Explore the differences and implications of these convergence types to deepen your understanding of infinite series behavior.
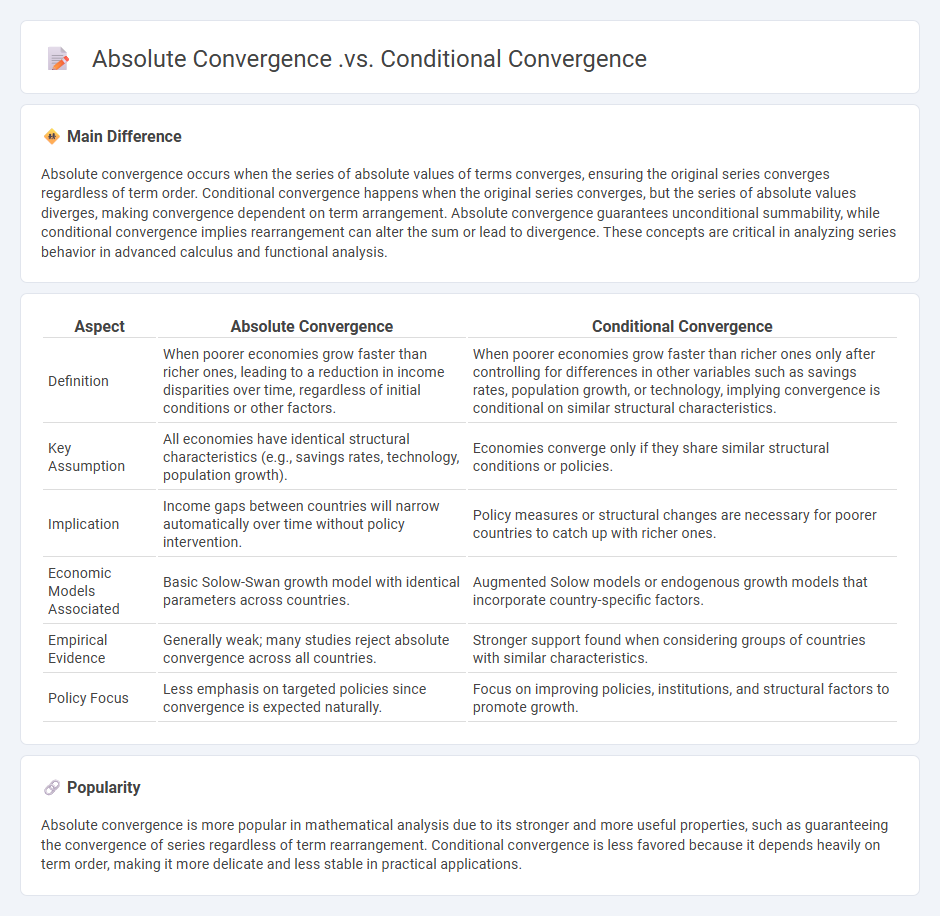
Main Difference
Absolute convergence occurs when the series of absolute values of terms converges, ensuring the original series converges regardless of term order. Conditional convergence happens when the original series converges, but the series of absolute values diverges, making convergence dependent on term arrangement. Absolute convergence guarantees unconditional summability, while conditional convergence implies rearrangement can alter the sum or lead to divergence. These concepts are critical in analyzing series behavior in advanced calculus and functional analysis.
Connection
Absolute convergence occurs when the series of absolute values of terms converges, ensuring the original series converges regardless of term order. Conditional convergence happens when a series converges, but not absolutely, indicating that rearranging terms can alter its sum. Understanding this connection is crucial in analysis, especially when applying tests like the Comparison Test or the Riemann Series Theorem.
Comparison Table
| Aspect | Absolute Convergence | Conditional Convergence |
|---|---|---|
| Definition | When poorer economies grow faster than richer ones, leading to a reduction in income disparities over time, regardless of initial conditions or other factors. | When poorer economies grow faster than richer ones only after controlling for differences in other variables such as savings rates, population growth, or technology, implying convergence is conditional on similar structural characteristics. |
| Key Assumption | All economies have identical structural characteristics (e.g., savings rates, technology, population growth). | Economies converge only if they share similar structural conditions or policies. |
| Implication | Income gaps between countries will narrow automatically over time without policy intervention. | Policy measures or structural changes are necessary for poorer countries to catch up with richer ones. |
| Economic Models Associated | Basic Solow-Swan growth model with identical parameters across countries. | Augmented Solow models or endogenous growth models that incorporate country-specific factors. |
| Empirical Evidence | Generally weak; many studies reject absolute convergence across all countries. | Stronger support found when considering groups of countries with similar characteristics. |
| Policy Focus | Less emphasis on targeted policies since convergence is expected naturally. | Focus on improving policies, institutions, and structural factors to promote growth. |
Absolute Convergence
Absolute convergence in economics refers to the hypothesis that poorer economies will grow at faster rates than richer ones, eventually leading to similar levels of per capita income. This concept is central to growth theory and suggests that differences in income levels diminish over time under conditions of similar savings rates, population growth, and technological progress. Empirical studies often analyze absolute convergence by examining GDP per capita across countries or regions over several decades. Key contributions to this field include the Solow-Swan growth model and cross-country regression analyses conducted by economists such as Robert Barro and Xavier Sala-i-Martin.
Conditional Convergence
Conditional convergence in economics refers to the concept that poorer economies will tend to grow faster than richer ones but only when they share similar structural characteristics such as savings rates, population growth, and technology levels. This theory contrasts with absolute convergence by emphasizing the importance of initial conditions and policies in determining growth trajectories. Empirical studies often use cross-country growth regressions, showing that countries with similar steady-state determinants exhibit convergence in per capita income over time. The Solow growth model underpins this concept by predicting convergence conditional on equivalent rates of investment and human capital accumulation.
Economic Growth Rates
Economic growth rates measure the annual percentage increase in a country's gross domestic product (GDP), reflecting the overall health and expansion of the economy. Key factors influencing growth rates include labor productivity, capital investment, technological innovation, and government policies. Historical data from the World Bank shows that emerging markets like India and China have sustained growth rates above 6% in recent decades, outpacing many developed economies with rates closer to 2-3%. Understanding these rates is critical for policymakers to design strategies that foster sustainable economic development and improve living standards.
Initial Income Levels
Initial income levels significantly influence economic growth trajectories and wealth distribution patterns within countries. Higher starting incomes often correlate with increased investment capacity, better access to education, and improved infrastructure development. Economies with low initial income levels may face challenges such as limited capital accumulation and persistent poverty traps, affecting long-term growth potential. Policymakers focus on income redistribution and inclusive growth strategies to address disparities stemming from varied initial income conditions.
Structural Factors
Structural factors in economics refer to the fundamental economic and institutional frameworks that shape the long-term growth and development of an economy. These include elements such as labor market rigidities, capital market imperfections, infrastructure quality, regulatory environment, and technological capabilities. Differences in education systems, industrial composition, and geographic location also significantly influence productivity and economic resilience. Understanding these factors is crucial for designing policies that address systemic challenges and promote sustainable economic progress.
Source and External Links
6.6 Absolute and Conditional Convergence - SFU Math Course Notes - A series \(\sum a_n\) converges absolutely if \(\sum |a_n|\) converges; if \(\sum a_n\) converges but \(\sum |a_n|\) diverges, the series converges conditionally, such as the alternating harmonic series.
Absolute Convergence vs Conditional Convergence vs Convergence - YouTube - Absolute convergence means the series formed by absolute values converges, guaranteeing the original series converges; conditional convergence means the original series converges but does not converge absolutely.
Calculus II - Absolute Convergence - Pauls Online Math Notes - Absolutely convergent series retain their sum under any rearrangement, while conditionally convergent series can be rearranged to converge to any real number, highlighting a key difference in their behavior.
FAQs
What is convergence in mathematical series?
Convergence in a mathematical series occurs when the sequence of partial sums approaches a specific finite limit as the number of terms increases indefinitely.
What is absolute convergence?
Absolute convergence occurs when the series of absolute values of a given series converges, meaning |a_n| converges.
What is conditional convergence?
Conditional convergence occurs when an infinite series converges only because its terms decrease in magnitude and alternate in sign, meaning the series converges but does not converge absolutely.
How do you test for absolute convergence?
Test for absolute convergence by checking if the series of absolute values \( \sum |a_n| \) converges. If \( \sum |a_n| \) converges, then the original series \( \sum a_n \) converges absolutely. Use comparison test, ratio test, root test, or integral test on \( \sum |a_n| \) to determine convergence.
What is an example of a conditionally convergent series?
The alternating harmonic series \(\sum_{n=1}^{\infty} (-1)^{n+1} \frac{1}{n}\) is an example of a conditionally convergent series.
Why is absolute convergence stronger than conditional convergence?
Absolute convergence is stronger than conditional convergence because it guarantees convergence of the series regardless of term rearrangement, while conditional convergence depends on the order of terms and may diverge if rearranged.
How does rearranging terms affect conditionally convergent series?
Rearranging terms of a conditionally convergent series can change its sum or cause divergence, as Riemann's rearrangement theorem states such series can be rearranged to converge to any real number or diverge.
 calledges.com
calledges.com