The Arrow-Debreu Model formalizes general equilibrium through complete markets and contingent commodities, ensuring existence and efficiency under uncertainty. Walrasian Equilibrium, rooted in excess demand functions and price adjustment mechanisms, characterizes market clearing in simplified settings without uncertainty. Explore deeper distinctions and applications to enhance your understanding of economic equilibrium theories.
Main Difference
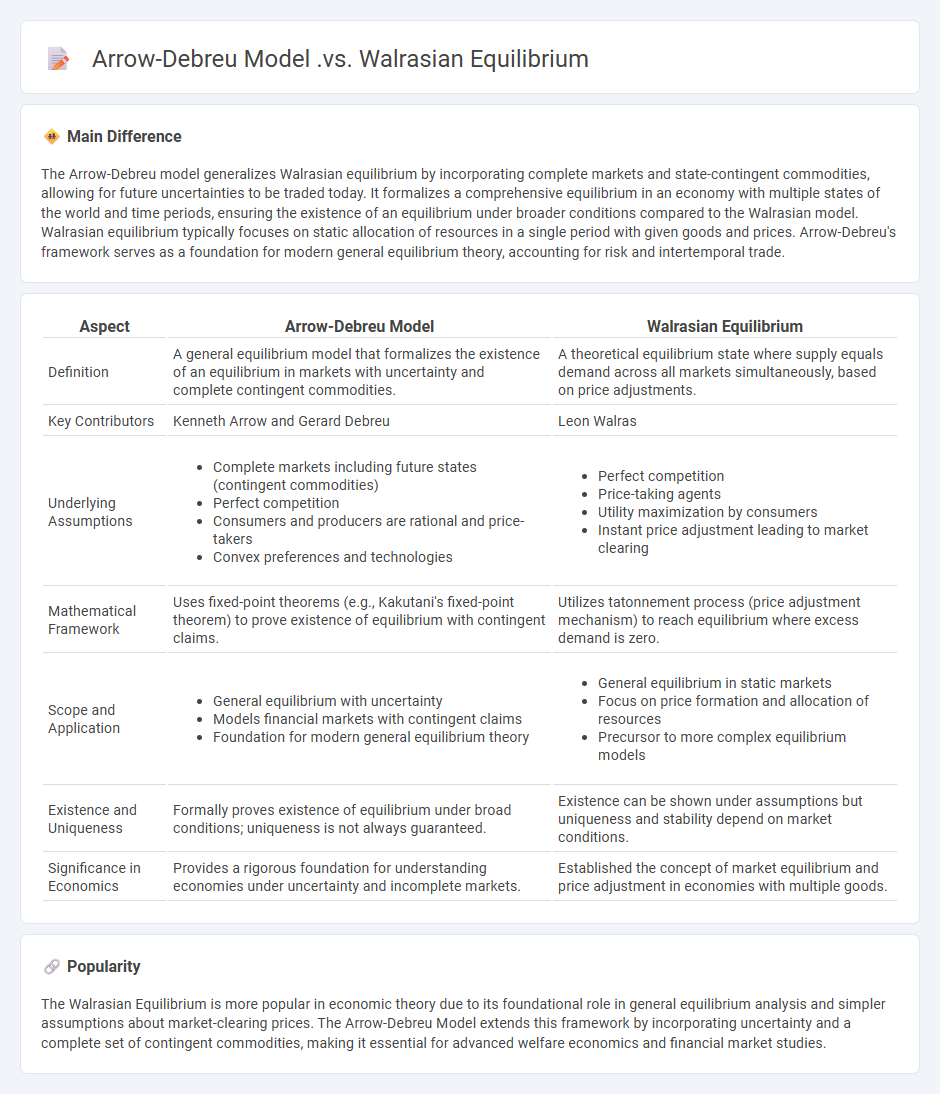
The Arrow-Debreu model generalizes Walrasian equilibrium by incorporating complete markets and state-contingent commodities, allowing for future uncertainties to be traded today. It formalizes a comprehensive equilibrium in an economy with multiple states of the world and time periods, ensuring the existence of an equilibrium under broader conditions compared to the Walrasian model. Walrasian equilibrium typically focuses on static allocation of resources in a single period with given goods and prices. Arrow-Debreu's framework serves as a foundation for modern general equilibrium theory, accounting for risk and intertemporal trade.
Connection
The Arrow-Debreu Model formalizes the existence of a Walrasian Equilibrium by proving that under certain conditions, a set of prices exists where market supply equals demand across all goods simultaneously. This model uses a complete set of contingent commodities to represent economies under uncertainty, extending Walrasian Equilibrium beyond deterministic settings. Both concepts serve as foundational pillars in general equilibrium theory, establishing criteria for efficient resource allocation in competitive markets.
Comparison Table
| Aspect | Arrow-Debreu Model | Walrasian Equilibrium |
|---|---|---|
| Definition | A general equilibrium model that formalizes the existence of an equilibrium in markets with uncertainty and complete contingent commodities. | A theoretical equilibrium state where supply equals demand across all markets simultaneously, based on price adjustments. |
| Key Contributors | Kenneth Arrow and Gerard Debreu | Leon Walras |
| Underlying Assumptions |
|
|
| Mathematical Framework | Uses fixed-point theorems (e.g., Kakutani's fixed-point theorem) to prove existence of equilibrium with contingent claims. | Utilizes tatonnement process (price adjustment mechanism) to reach equilibrium where excess demand is zero. |
| Scope and Application |
|
|
| Existence and Uniqueness | Formally proves existence of equilibrium under broad conditions; uniqueness is not always guaranteed. | Existence can be shown under assumptions but uniqueness and stability depend on market conditions. |
| Significance in Economics | Provides a rigorous foundation for understanding economies under uncertainty and incomplete markets. | Established the concept of market equilibrium and price adjustment in economies with multiple goods. |
Complete Markets
Complete markets enable the allocation of risk through the trading of a full set of contingent claims for every possible state of the world. In such markets, individuals can insure against all future uncertainties, leading to Pareto efficient outcomes and optimal resource distribution. Theoretical models assume completeness to simplify equilibrium analysis, yet real-world markets often face frictions preventing full completion. Empirical studies on financial derivatives highlight efforts to approximate market completeness by expanding asset classes and improving liquidity.
Contingent Commodities
Contingent commodities refer to goods or services whose delivery depends on specific future events or conditions, influencing their valuation and trade dynamics. They are often analyzed in economics within the framework of contingent claims and risk management, connecting commodity markets with financial derivatives. Pricing of contingent commodities incorporates uncertainty and probabilistic outcomes, making them critical in sectors like energy, agriculture, and insurance. Economists utilize contingent commodities to model and mitigate risks associated with supply disruptions, weather variability, and geopolitical events impacting commodity availability.
General Equilibrium
General equilibrium refers to the state in an economy where supply and demand across all markets simultaneously balance, resulting in an overall allocation of resources that is efficient. It was formalized by Leon Walras in the late 19th century and further developed through the Arrow-Debreu model, which provides conditions for existence and stability of equilibrium. The model assumes perfect competition, complete markets, and rational agents optimizing utility or profit. General equilibrium analysis helps economists understand the interdependence of markets and the effects of policy changes on the entire economy.
State-Contingent Claims
State-contingent claims represent financial instruments whose payoffs depend on specific states of the world, defining future economic scenarios. They play a crucial role in economic theory by facilitating allocation of risk and optimizing resource distribution under uncertainty, as demonstrated in Arrow-Debreu models. These claims enable agents to hedge against state-specific risks through contingent contracts, enhancing market completeness. Empirical studies highlight their application in diverse markets, including derivatives pricing and insurance-linked securities, emphasizing their significance in modern financial economics.
Existence and Uniqueness
Existence and uniqueness theorems are fundamental in economic theory, ensuring that equilibrium states, such as market equilibria or solutions to optimization problems, are well-defined and stable. In general equilibrium theory, the Arrow-Debreu model guarantees the existence of an equilibrium under convex preferences and complete markets, while unique equilibrium outcomes often require strict convexity or monotonicity conditions. These mathematical results underpin the predictability and consistency of economic models, aiding in comparative statics and welfare analysis. Economists rely on fixed-point theorems like Brouwer and Kakutani to prove existence and use conditions on utility functions and production sets to establish uniqueness.
Source and External Links
Arrow-Debreu Model Definition & Examples - Quickonomics - The Arrow-Debreu model is a general equilibrium framework where prices for all goods and services are set so supply equals demand in every market, even accounting for differences in time, location, and uncertainty through state-contingent contracts.
Competitive equilibrium - Wikipedia - Competitive equilibrium (also called Walrasian equilibrium) is the standard concept where prices adjust until supply equals demand in all markets, and it was formalized in its existence proof by Arrow and Debreu.
Arrow-Debreu Model | Encyclopedia.com - The Arrow-Debreu model is a formalized Walrasian system that proves the existence of a competitive equilibrium under specific conditions, and is sometimes called the Arrow-Debreu-McKenzie model due to parallel work by McKenzie.
FAQs
What is the Arrow-Debreu Model?
The Arrow-Debreu Model is a foundational economic framework that mathematically proves the existence of a general equilibrium in competitive markets with complete markets and perfect information.
What defines a Walrasian Equilibrium?
A Walrasian Equilibrium is defined by a price vector where the aggregate supply equals aggregate demand for every good in a perfectly competitive market, ensuring no excess demand or surplus.
How does the Arrow-Debreu Model differ from Walrasian Equilibrium?
The Arrow-Debreu Model generalizes Walrasian Equilibrium by incorporating uncertainty and time through state-contingent commodities, providing existence proofs for equilibrium under complete markets, while Walrasian Equilibrium focuses on static markets with fixed goods and prices without explicitly modeling uncertainty.
What assumptions underpin the Arrow-Debreu Model?
The Arrow-Debreu Model assumes complete markets, perfect competition, rational agents with complete information, no externalities, and convex preferences ensuring equilibrium existence and Pareto efficiency.
What are the key features of a Walrasian market?
A Walrasian market features price-taking agents, a central auctioneer who adjusts prices to achieve market equilibrium, goods traded at equilibrium prices, and the existence of a unique equilibrium where supply equals demand across all markets.
How do both models address uncertainty and time?
The Bayesian model quantifies uncertainty through probability distributions and updates beliefs over time using Bayes' theorem, while the Markov model captures time-dependent processes by modeling state transitions with associated probabilities in discrete time steps.
Why are these models important in general equilibrium theory?
These models are important in general equilibrium theory because they analyze how supply and demand interact across multiple markets to determine prices and allocate resources efficiently.
 calledges.com
calledges.com