Sequential logic circuits store and process information based on input sequences and previous states, making them essential for memory and timing applications. Combinational logic circuits, on the other hand, generate outputs solely from the current inputs without memory, fundamental in arithmetic and data processing operations. Explore detailed comparisons and applications to understand their roles in digital system design.
Main Difference
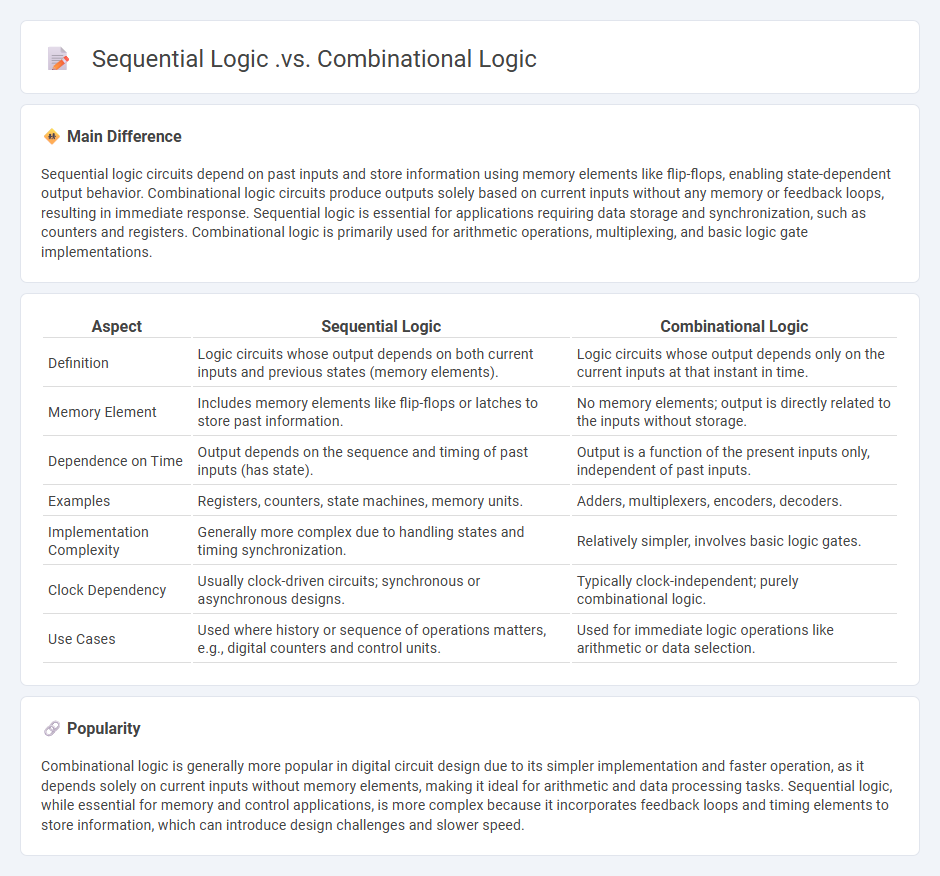
Sequential logic circuits depend on past inputs and store information using memory elements like flip-flops, enabling state-dependent output behavior. Combinational logic circuits produce outputs solely based on current inputs without any memory or feedback loops, resulting in immediate response. Sequential logic is essential for applications requiring data storage and synchronization, such as counters and registers. Combinational logic is primarily used for arithmetic operations, multiplexing, and basic logic gate implementations.
Connection
Sequential logic relies on combinational logic circuits to process inputs and generate outputs based on current signals and past states stored in memory elements. Combinational logic determines the next state and output values by evaluating inputs and feedback from flip-flops or latches in sequential circuits. This interaction enables complex state-dependent behaviors critical for digital systems like finite state machines, counters, and memory devices.
Comparison Table
| Aspect | Sequential Logic | Combinational Logic |
|---|---|---|
| Definition | Logic circuits whose output depends on both current inputs and previous states (memory elements). | Logic circuits whose output depends only on the current inputs at that instant in time. |
| Memory Element | Includes memory elements like flip-flops or latches to store past information. | No memory elements; output is directly related to the inputs without storage. |
| Dependence on Time | Output depends on the sequence and timing of past inputs (has state). | Output is a function of the present inputs only, independent of past inputs. |
| Examples | Registers, counters, state machines, memory units. | Adders, multiplexers, encoders, decoders. |
| Implementation Complexity | Generally more complex due to handling states and timing synchronization. | Relatively simpler, involves basic logic gates. |
| Clock Dependency | Usually clock-driven circuits; synchronous or asynchronous designs. | Typically clock-independent; purely combinational logic. |
| Use Cases | Used where history or sequence of operations matters, e.g., digital counters and control units. | Used for immediate logic operations like arithmetic or data selection. |
State Dependency
State dependency in engineering refers to the phenomenon where the behavior or output of a system depends on its current state or condition, rather than solely on its inputs. This concept is critical in control systems, signal processing, and material science, where system responses vary based on previous states, enabling accurate modeling of dynamic behaviors. State-dependent models, such as state machines and differential equations, facilitate the prediction and control of complex engineering systems across various applications. Effective state dependency analysis improves system reliability, performance, and adaptability in real-time engineering solutions.
Memory Elements
Memory elements in engineering serve as fundamental components for data storage and retrieval within digital systems, including flip-flops, latches, and registers. These devices retain binary information through stable states, enabling sequential logic operations essential in microprocessors, memory units, and digital signal processing. Modern memory elements employ technologies like CMOS and SRAM to balance speed, power efficiency, and scalability. Their design impacts computing performance, influencing system responsiveness and overall reliability in embedded and general-purpose computing applications.
Output Determination
Output determination in engineering involves accurately calculating the final product or result of a system based on input variables and system parameters. Techniques such as mathematical modeling, simulation, and statistical analysis are commonly used to predict performance metrics in fields like control systems, mechanical design, and electrical engineering. Precise output determination enhances system efficiency, reliability, and optimization during the design and operational phases. Real-world applications include power generation output estimation, manufacturing process yields, and signal processing results.
Timing Control
Timing control in engineering ensures precise synchronization of processes and systems, critical in electronics, robotics, and manufacturing. It involves managing signal delays, clock distribution, and timing analysis to optimize performance and minimize errors. Techniques like phase-locked loops (PLLs) and delay-locked loops (DLLs) help maintain stable timing references in integrated circuits. Effective timing control improves system reliability, reduces latency, and enhances overall operational efficiency.
Circuit Complexity
Circuit complexity in engineering measures the resources required to implement Boolean functions using digital circuits, focusing on minimizing gate count and depth to optimize performance and cost. It plays a critical role in VLSI design, impacting power consumption, speed, and area efficiency of integrated circuits. Advances in circuit complexity theory guide the development of efficient algorithms for logic synthesis and optimization in hardware engineering. Understanding circuit complexity enables engineers to design scalable and reliable systems for applications ranging from microprocessors to communication devices.
Source and External Links
Difference Between Combinational and Sequential Circuits - Vedantu - Combinational logic depends only on current inputs with no memory, making it simpler and faster, while sequential logic depends on current inputs and past stored data, involving clocks and more complex designs.
Combinational vs Sequential Circuits: Key Differences - Combinational circuits generate outputs solely based on current inputs instantly, and sequential circuits use memory elements like flip-flops to store past inputs influencing future outputs.
Difference between Combinational and Sequential Circuit - GeeksforGeeks - Combinational circuits perform immediate operations based only on present inputs without memory, while sequential circuits use memory elements to incorporate past inputs, making outputs dependent on both present and previous states.
FAQs
What is logic in digital circuits?
Logic in digital circuits refers to the use of Boolean algebra to perform operations on binary signals, enabling the design and functioning of gates, circuits, and systems that process digital data.
What is the difference between sequential logic and combinational logic?
Sequential logic depends on past inputs and stores information using memory elements, producing outputs based on current and previous states; combinational logic outputs depend solely on the current inputs without memory or feedback.
What are examples of sequential logic circuits?
Examples of sequential logic circuits include flip-flops, counters, shift registers, and memory units.
What are examples of combinational logic circuits?
Examples of combinational logic circuits include adders, multiplexers, demultiplexers, encoders, decoders, and comparators.
How does memory work in sequential logic?
Memory in sequential logic is achieved through storage elements like flip-flops and latches that store binary states based on clock signals, enabling circuits to maintain and update information over time.
Why is timing important in sequential logic?
Timing in sequential logic ensures accurate synchronization of data storage and state transitions, preventing errors and maintaining reliable circuit operation.
Where are sequential and combinational logic used?
Sequential logic is used in memory units, counters, and flip-flops for storing and processing state information, while combinational logic is used in arithmetic circuits, multiplexers, and encoders for performing operations based solely on current inputs.
 calledges.com
calledges.com