B+ Trees optimize disk-based data storage with their multi-level indexing and strict balance, making them ideal for database systems and file indexing. Red-Black Trees maintain balance via color-coding rules in binary search trees, ensuring efficient in-memory data operations and dynamic data sets. Explore the structural and performance differences between B+ Trees and Red-Black Trees to understand their distinct use cases and advantages.
Main Difference
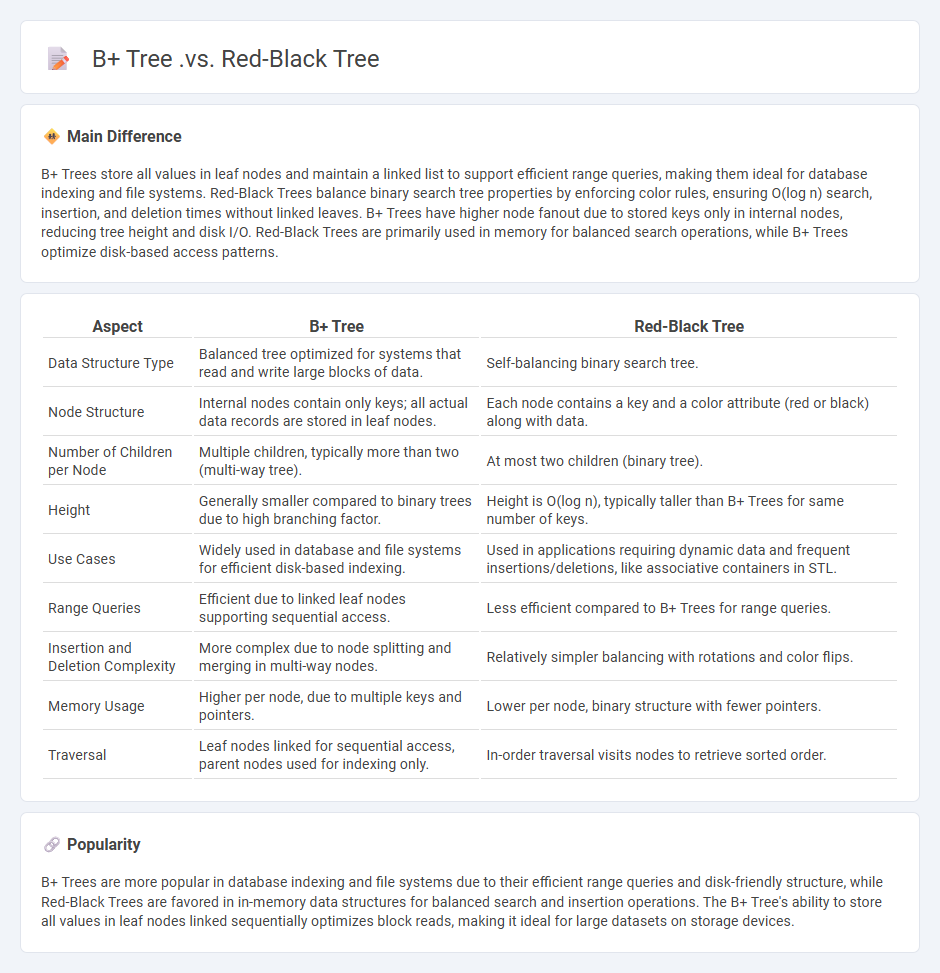
B+ Trees store all values in leaf nodes and maintain a linked list to support efficient range queries, making them ideal for database indexing and file systems. Red-Black Trees balance binary search tree properties by enforcing color rules, ensuring O(log n) search, insertion, and deletion times without linked leaves. B+ Trees have higher node fanout due to stored keys only in internal nodes, reducing tree height and disk I/O. Red-Black Trees are primarily used in memory for balanced search operations, while B+ Trees optimize disk-based access patterns.
Connection
B+ Trees and Red-Black Trees both belong to the family of balanced tree data structures used in computer science to maintain sorted data and allow efficient insertion, deletion, and search operations. A Red-Black Tree is a type of self-balancing binary search tree that ensures O(log n) time complexity for these operations by enforcing color and structural properties, while a B+ Tree is a balanced tree optimized for systems that read and write large blocks of data, commonly used in databases and file systems. The connection lies in their common goal of maintaining balanced height and efficient data retrieval, with B+ Trees extending the concept to multiway trees and Red-Black Trees implementing balance through color properties in binary form.
Comparison Table
| Aspect | B+ Tree | Red-Black Tree |
|---|---|---|
| Data Structure Type | Balanced tree optimized for systems that read and write large blocks of data. | Self-balancing binary search tree. |
| Node Structure | Internal nodes contain only keys; all actual data records are stored in leaf nodes. | Each node contains a key and a color attribute (red or black) along with data. |
| Number of Children per Node | Multiple children, typically more than two (multi-way tree). | At most two children (binary tree). |
| Height | Generally smaller compared to binary trees due to high branching factor. | Height is O(log n), typically taller than B+ Trees for same number of keys. |
| Use Cases | Widely used in database and file systems for efficient disk-based indexing. | Used in applications requiring dynamic data and frequent insertions/deletions, like associative containers in STL. |
| Range Queries | Efficient due to linked leaf nodes supporting sequential access. | Less efficient compared to B+ Trees for range queries. |
| Insertion and Deletion Complexity | More complex due to node splitting and merging in multi-way nodes. | Relatively simpler balancing with rotations and color flips. |
| Memory Usage | Higher per node, due to multiple keys and pointers. | Lower per node, binary structure with fewer pointers. |
| Traversal | Leaf nodes linked for sequential access, parent nodes used for indexing only. | In-order traversal visits nodes to retrieve sorted order. |
Balanced Search Tree
A balanced search tree is a data structure that maintains sorted data for efficient search, insertion, and deletion operations. Common types include AVL trees, Red-Black trees, and B-trees, each ensuring logarithmic time complexity by keeping the tree height balanced. These trees are fundamental in database indexing, memory management, and implementing associative arrays. Their structure guarantees O(log n) time complexity for critical operations, optimizing performance in large-scale computing applications.
Multi-way Branching
Multi-way branching in computer programming allows a program to choose from multiple execution paths based on the value of a variable or expression. Common constructs for multi-way branching include switch-case statements in languages like C, C++, and Java, which optimize decision-making by directly jumping to relevant code blocks. This branching mechanism enhances code readability and efficiency by reducing nested if-else statements. Modern compilers often convert switch-case statements into jump tables or lookup tables for faster execution.
Disk-based Storage
Disk-based storage refers to data storage technologies that record information on magnetic or optical disks. Common implementations include hard disk drives (HDDs), which use magnetic storage, and solid-state drives (SSDs) that, while not disk-based, often complement disk storage systems in computers. HDDs offer high capacity at a low cost per gigabyte, making them suitable for storing large datasets and backups. The adoption of disk-based storage remains critical in enterprise data centers and personal computing for persistent data retention.
Height Balancing
Height balancing in computer science refers to techniques used to maintain an optimal tree height for data structures like AVL trees and Red-Black trees. These self-balancing binary search trees ensure that operations such as search, insertion, and deletion run in O(log n) time by preventing the tree from becoming skewed. Algorithms perform rotations to rebalance the tree after insertions and deletions, preserving efficient data retrieval. Maintaining balanced height is crucial in large-scale database indexing and memory management systems to optimize performance.
Insertion & Deletion Efficiency
Insertion and deletion efficiency in computer science directly impacts data structure performance, particularly in arrays, linked lists, and trees. Linked lists offer O(1) time complexity for insertion and deletion when the node reference is known, whereas arrays require O(n) due to element shifting. Balanced trees like AVL and Red-Black trees maintain O(log n) efficiency for both operations by rebalancing nodes during insertions and deletions. Optimizing these operations is critical in database indexing and dynamic memory allocation systems.
Source and External Links
B-Tree - A self-balancing tree data structure that maintains sorted data and is particularly efficient for secondary storage access by minimizing the number of node accesses.
Red-Black Tree - A self-balancing binary search tree that ensures efficient data retrieval and manipulation by maintaining a balance between the height of different branches using color-coding.
B-Tree vs Red-Black Tree - B-trees allow multiple children per node, making them suitable for disk storage, while Red-Black Trees are more suitable for in-memory data structures like `std::map` and `std::set`.
FAQs
What is a B+ Tree?
A B+ Tree is a balanced tree data structure that maintains sorted data and allows efficient insertion, deletion, and search operations, commonly used in databases and file systems.
What is a Red-Black Tree?
A Red-Black Tree is a self-balancing binary search tree where each node contains an extra bit for denoting the color, either red or black, ensuring balanced tree height and guaranteeing O(log n) time complexity for insertion, deletion, and search operations.
How does a B+ Tree differ from a Red-Black Tree?
A B+ Tree is a balanced tree data structure optimized for disk-based storage with multi-way nodes and stores all keys in leaf nodes linked for sequential access, while a Red-Black Tree is a binary search tree with color properties ensuring balanced height and efficient in-memory search and insertion operations.
What are the use cases for B+ Tree compared to Red-Black Tree?
B+ Trees are primarily used in database indexing and file systems due to their efficient disk-based range queries and sequential access, while Red-Black Trees are preferred for in-memory data structures requiring balanced search, insert, and delete operations with O(log n) complexity.
How do B+ Trees and Red-Black Trees handle data insertion?
B+ Trees handle data insertion by locating the appropriate leaf node, inserting the key in sorted order, and splitting the leaf node if it exceeds capacity, then propagating splits upward to maintain balance. Red-Black Trees handle insertion by performing a standard binary search tree insert followed by color assignments and rotations to preserve red-black properties ensuring balanced height.
Which tree provides faster search performance?
Binary Search Tree (BST) provides faster search performance in average cases due to its logarithmic time complexity O(log n).
Why choose B+ Tree over Red-Black Tree in databases?
B+ Tree is preferred over Red-Black Tree in databases due to its optimized disk I/O with higher fan-out, allowing efficient range queries and sequential access by storing all values in leaf nodes linked for fast traversal.
 calledges.com
calledges.com