Canonical form represents a standardized mathematical expression where every element follows a unique, simplified pattern, such as the canonical representation of a Boolean function using minterms. Normal form refers to logical expressions arranged according to specific rules like Conjunctive Normal Form (CNF) or Disjunctive Normal Form (DNF), essential in logic programming and automated theorem proving. Explore deeper insights into how canonical and normal forms optimize computational logic and data representation.
Main Difference
Canonical form is a standardized or simplified representation of a mathematical object or logical expression that is unique for each equivalence class, ensuring consistency in analysis. Normal form refers to a structured version of data, database schemas, or logical formulas designed to reduce redundancy and improve clarity by adhering to specific rules or constraints. Canonical forms often serve as a basis for comparison, while normal forms focus on optimizing structure and eliminating anomalies. Both concepts are crucial in database normalization, logic simplification, and algebraic computation for enhancing data integrity and computational efficiency.
Connection
Canonical form and normal form both represent standardized ways to express mathematical objects, ensuring consistency and simplicity in interpretation. Canonical form provides a unique representation for an object, often used in algebra and logic to test equivalences, while normal form emphasizes a simplified or reduced version maintaining essential properties. Their connection lies in transforming expressions or data structures into these optimized formats to facilitate comparison, computation, or theoretical analysis.
Comparison Table
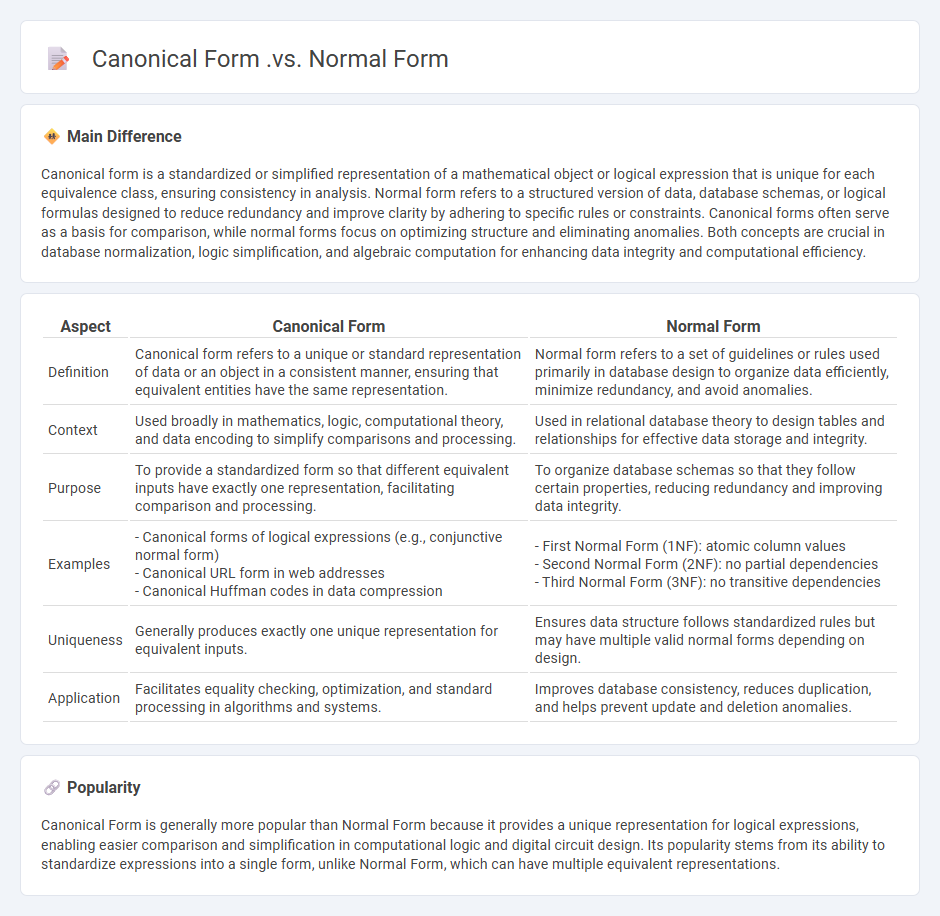
| Aspect | Canonical Form | Normal Form |
|---|---|---|
| Definition | Canonical form refers to a unique or standard representation of data or an object in a consistent manner, ensuring that equivalent entities have the same representation. | Normal form refers to a set of guidelines or rules used primarily in database design to organize data efficiently, minimize redundancy, and avoid anomalies. |
| Context | Used broadly in mathematics, logic, computational theory, and data encoding to simplify comparisons and processing. | Used in relational database theory to design tables and relationships for effective data storage and integrity. |
| Purpose | To provide a standardized form so that different equivalent inputs have exactly one representation, facilitating comparison and processing. | To organize database schemas so that they follow certain properties, reducing redundancy and improving data integrity. |
| Examples | - Canonical forms of logical expressions (e.g., conjunctive normal form) - Canonical URL form in web addresses - Canonical Huffman codes in data compression |
- First Normal Form (1NF): atomic column values - Second Normal Form (2NF): no partial dependencies - Third Normal Form (3NF): no transitive dependencies |
| Uniqueness | Generally produces exactly one unique representation for equivalent inputs. | Ensures data structure follows standardized rules but may have multiple valid normal forms depending on design. |
| Application | Facilitates equality checking, optimization, and standard processing in algorithms and systems. | Improves database consistency, reduces duplication, and helps prevent update and deletion anomalies. |
Data Representation
Data representation in computers is the method of encoding information in binary format using bits (0s and 1s). Common representations include integers, floating-point numbers, characters (using ASCII or Unicode), and complex data structures. Memory storage and processing rely on these standardized formats to ensure accurate computation and efficient data manipulation. Understanding data representation is critical for optimizing algorithm performance and hardware utilization.
Uniqueness
Uniqueness in computer science refers to the property of data or identifiers being one-of-a-kind within a given system or database to prevent duplication and ensure accurate referencing. Unique keys, such as primary keys in relational databases, play a critical role in maintaining data integrity by uniquely identifying records. Algorithms that generate unique identifiers, like UUIDs (Universally Unique Identifiers), are essential for distributed computing environments to avoid conflicts. Ensuring uniqueness enhances data consistency, security, and efficient retrieval in computer applications.
Standardization
Standardization in computer technology ensures compatibility and interoperability among hardware, software, and network systems. It involves establishing uniform technical specifications such as IEEE 802.11 for wireless networking and USB standards for device connectivity. These standards facilitate seamless communication, improve system reliability, and reduce development costs across diverse computing platforms. Organizations like the International Organization for Standardization (ISO) and the Institute of Electrical and Electronics Engineers (IEEE) play critical roles in developing and maintaining these standards.
Equivalence
Equivalence in computer science refers to the concept where two expressions, algorithms, or systems produce the same output or exhibit identical behavior under the same conditions. It is fundamental in compiler optimization, formal verification, and testing, ensuring that code transformations or refactorings preserve functionality. Techniques such as equivalence checking use mathematical models and automated tools to verify that two representations of a program are functionally identical. This concept is crucial for maintaining software reliability and correctness in complex computing environments.
Transformation
Transformation in computer science refers to the systematic process of converting data, models, or algorithms from one format or structure to another to improve functionality, compatibility, or performance. This process includes data transformation operations such as normalization, aggregation, and encoding, which are essential in data preprocessing for machine learning and database management. Code transformation involves refactoring or compiling source code to enhance efficiency, maintainability, or portability across different platforms. Model transformation, a key aspect of model-driven engineering, automates the conversion between abstract representations to facilitate software development and system integration.
Source and External Links
Canonical form - Wikipedia - Canonical form specifies a unique representation for every object, while normal form specifies a form without the requirement of uniqueness; canonical forms allow unique identification and equality testing, whereas normal forms are a weaker notion often used when uniqueness is difficult to achieve.
Canonical and Standard Form - GeeksforGeeks - In Boolean algebra, canonical form is unique and completely represents a function but can be complex, while standard (normal) form is simpler and more efficient but not unique and may be ambiguous.
Canonical normal form - Wikipedia - Canonical normal forms in Boolean algebra include canonical disjunctive normal form and canonical conjunctive normal form, both of which express Boolean functions in unique standardized ways useful for simplification and circuit optimization.
FAQs
What is canonical form in mathematics or logic?
Canonical form in mathematics or logic is a standard or simplest representation of an object, expression, or formula that is unique and unambiguous, facilitating comparison and classification.
What is normal form in mathematics or logic?
Normal form in mathematics or logic is a standardized or canonical representation of expressions, formulas, or data structures that simplifies comparison, manipulation, and analysis.
How does canonical form differ from normal form?
Canonical form is a unique, standardized representation of a mathematical object ensuring one-to-one correspondence, while normal form is a simplified or standardized version that may not be unique but facilitates easier analysis or comparison.
Why is canonical form useful in computation?
Canonical form ensures unique representation of data or expressions, simplifying comparison, optimization, storage, and algorithmic processing in computation.
What are examples of canonical and normal forms?
Examples of canonical forms include Jordan normal form, Smith normal form, and Hermite normal form. Examples of normal forms include Boyce-Codd normal form (BCNF) and Third normal form (3NF) in database design.
When should you use canonical form over normal form?
Use canonical form when you need a standardized, unique representation for mathematical expressions or matrices to simplify comparison, classification, or computation; choose normal form for general simplification or when the canonical form is computationally expensive or unnecessary.
How do transformations between canonical and normal forms work?
Transformations between canonical and normal forms involve applying specific algorithms to convert logical expressions or data structures into standardized formats that preserve semantic equivalence, enabling consistent analysis and optimization.
 calledges.com
calledges.com