Finite State Machines (FSMs) are computational models characterized by a finite number of states and transitions, ideal for recognizing regular languages and implementing control logic in software and hardware. Turing Machines extend this capability with an infinite tape for memory, enabling the simulation of any algorithm and recognition of a broader class of languages known as recursively enumerable languages. Explore the fundamental differences in computational power, memory use, and application domains to deepen your understanding of FSMs versus Turing Machines.
Main Difference
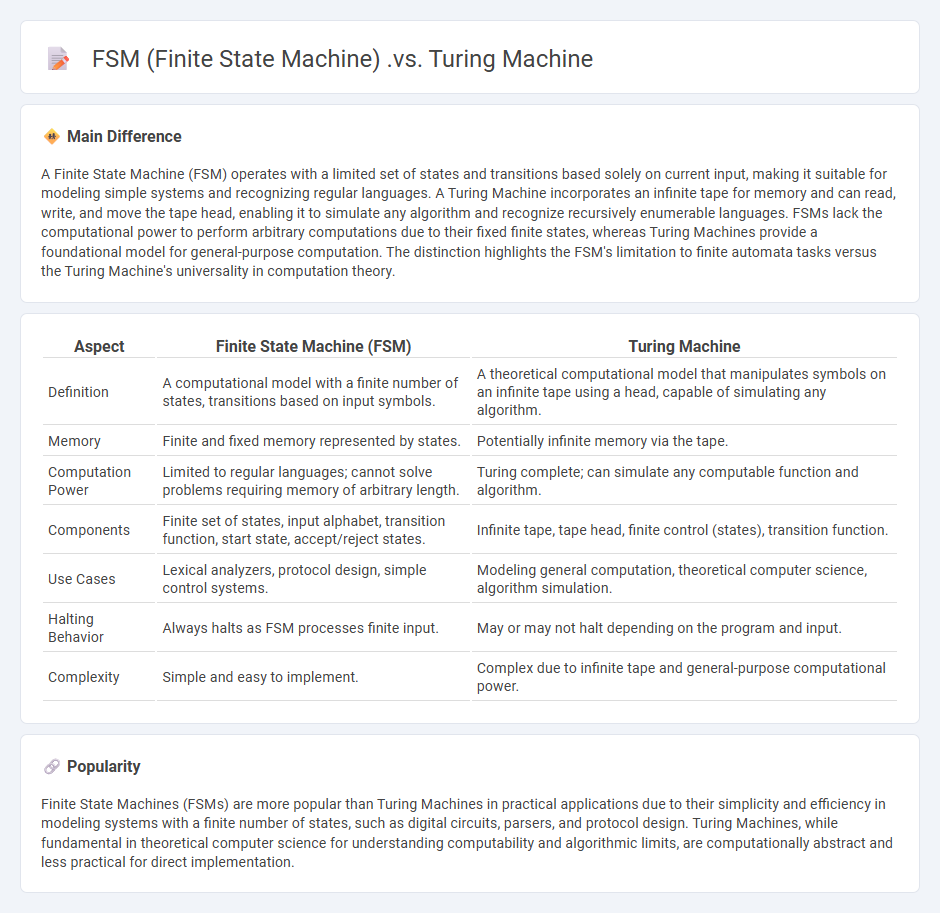
A Finite State Machine (FSM) operates with a limited set of states and transitions based solely on current input, making it suitable for modeling simple systems and recognizing regular languages. A Turing Machine incorporates an infinite tape for memory and can read, write, and move the tape head, enabling it to simulate any algorithm and recognize recursively enumerable languages. FSMs lack the computational power to perform arbitrary computations due to their fixed finite states, whereas Turing Machines provide a foundational model for general-purpose computation. The distinction highlights the FSM's limitation to finite automata tasks versus the Turing Machine's universality in computation theory.
Connection
Finite State Machines (FSMs) are foundational models in computational theory that represent systems with a finite number of states and transitions based on input symbols. Turing Machines extend the concept of FSMs by incorporating an infinite tape for memory, enabling them to perform more complex computations and model algorithmic processes. Both models formalize state transitions driven by input but differ in computational power, with Turing Machines being capable of solving problems beyond the scope of FSMs.
Comparison Table
| Aspect | Finite State Machine (FSM) | Turing Machine |
|---|---|---|
| Definition | A computational model with a finite number of states, transitions based on input symbols. | A theoretical computational model that manipulates symbols on an infinite tape using a head, capable of simulating any algorithm. |
| Memory | Finite and fixed memory represented by states. | Potentially infinite memory via the tape. |
| Computation Power | Limited to regular languages; cannot solve problems requiring memory of arbitrary length. | Turing complete; can simulate any computable function and algorithm. |
| Components | Finite set of states, input alphabet, transition function, start state, accept/reject states. | Infinite tape, tape head, finite control (states), transition function. |
| Use Cases | Lexical analyzers, protocol design, simple control systems. | Modeling general computation, theoretical computer science, algorithm simulation. |
| Halting Behavior | Always halts as FSM processes finite input. | May or may not halt depending on the program and input. |
| Complexity | Simple and easy to implement. | Complex due to infinite tape and general-purpose computational power. |
State Complexity
State complexity in computer science measures the number of states required by an automaton or computational model to recognize a particular language or perform a specific task. It is a critical factor in automata theory, influencing the design and efficiency of finite automata, pushdown automata, and Turing machines. Research indicates that minimizing state complexity can significantly optimize algorithms in natural language processing and pattern recognition. For instance, deterministic finite automata (DFA) for regular languages often exhibit exponential state complexity compared to nondeterministic finite automata (NFA).
Memory Capability
Memory capability in computers refers to the amount of data that a system's memory can store and access efficiently. It encompasses both volatile memory, such as RAM, which temporarily holds data for active processes, and non-volatile memory, like SSDs or HDDs, which store data persistently. High memory capacity enhances multitasking, speeds up data retrieval, and improves overall system performance, essential for applications requiring large datasets or complex computations. Advances in memory technology, including DDR5 RAM and NVMe SSDs, continue to push the boundaries of memory capability in modern computing systems.
Computation Power
Computation power in computers refers to the capacity of a system's hardware and software to process data and execute complex algorithms efficiently. Modern computers rely on multi-core processors, high-frequency CPUs, and advanced GPUs to deliver superior computational performance. The increase in computation power enables faster data analysis, real-time processing, and supports applications such as artificial intelligence, scientific simulations, and big data analytics. Benchmarking metrics like FLOPS (floating-point operations per second) and clock speed measured in gigahertz (GHz) provide quantifiable indicators of a computer's computation capabilities.
Tape vs. Transition
Tape storage remains a cost-effective solution for large-scale data archiving, offering high capacity and long retention periods with modern LTO (Linear Tape-Open) generations reaching up to 45 TB compressed per cartridge. Transitioning to solid-state drives (SSDs) and cloud storage improves access speed and data retrieval times, essential for real-time computing and big data analytics. Enterprise environments often implement hybrid storage architectures to balance the durability of tape with the performance of SSDs and cloud platforms. Tape's energy efficiency and offline data protection continue to make it valuable for disaster recovery and regulatory compliance in IT infrastructures.
Language Recognition
Language recognition in computer science involves the automated identification of spoken or written languages using algorithms and machine learning models. Techniques such as phoneme recognition, n-gram analysis, and deep neural networks enhance accuracy in processing diverse linguistic inputs. Large datasets like the Common Voice corpus and OpenSLR provide essential training material for improving recognition systems. Advances in natural language processing (NLP) enable applications in speech-to-text, multilingual translation, and voice-activated assistants.
Source and External Links
## Overview of FSM and Turing MachineFinite-state machine - Wikipedia - A finite-state machine is a mathematical model with a finite number of states, used for tasks like pattern matching and text processing.
## Key DifferencesDifference Between Finite Automata and Turing Machine - This article highlights that while Finite Automata recognize regular languages, Turing Machines can handle more complex languages like context-free and context-sensitive languages.
## Comparative PowerFSMs and Turing Machines - UNC Computational Systems Biology - A Turing Machine is more powerful than an FSM, as it can simulate an FSM and more by using an infinite tape, allowing it to process complex computations.
 calledges.com
calledges.com