Lambda Calculus and Turing Machines represent foundational models of computation, each defining the limits of what can be computed algorithmically. Lambda Calculus uses function abstraction and application as core principles, enabling the expression of computable functions through symbolic expressions. Explore the distinctions and connections between these pivotal theories to understand the evolution of computational theory.
Main Difference
Lambda Calculus focuses on function abstraction and application as a model of computation, utilizing variable binding and substitution to express computation purely through functions. Turing Machines operate based on a finite set of states, an infinite tape, and a read-write head, simulating algorithmic processes through state transitions and symbol manipulations. Lambda Calculus emphasizes expressiveness in functional programming, while Turing Machines provide a more mechanical step-by-step model of algorithm execution. Both models are computationally equivalent but differ fundamentally in representation and operational style.
Connection
Lambda Calculus and Turing Machines are foundational models of computation that establish the theoretical limits of what can be computed. Both frameworks are equivalent in computational power, meaning any function computable by a Turing Machine can also be expressed using Lambda Calculus, reflecting the Church-Turing thesis. This equivalence highlights their central role in formalizing algorithms and understanding computability in computer science.
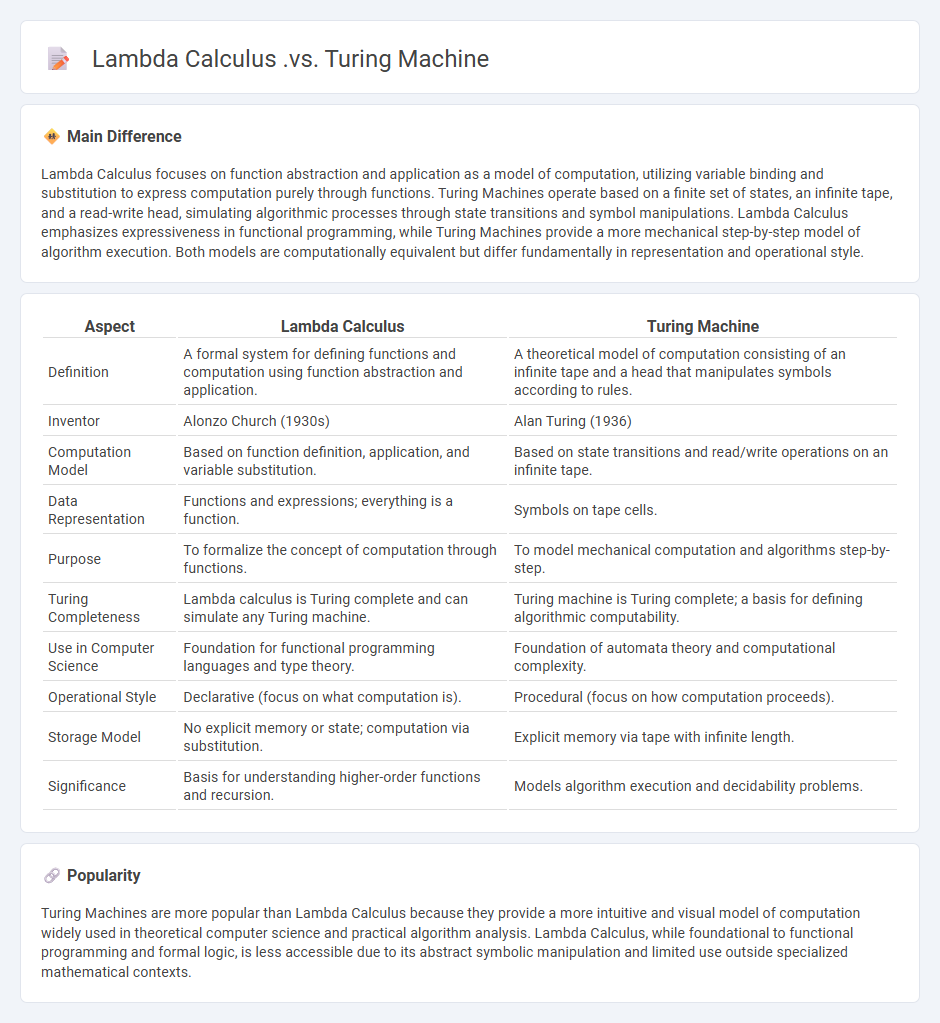
Comparison Table
| Aspect | Lambda Calculus | Turing Machine |
|---|---|---|
| Definition | A formal system for defining functions and computation using function abstraction and application. | A theoretical model of computation consisting of an infinite tape and a head that manipulates symbols according to rules. |
| Inventor | Alonzo Church (1930s) | Alan Turing (1936) |
| Computation Model | Based on function definition, application, and variable substitution. | Based on state transitions and read/write operations on an infinite tape. |
| Data Representation | Functions and expressions; everything is a function. | Symbols on tape cells. |
| Purpose | To formalize the concept of computation through functions. | To model mechanical computation and algorithms step-by-step. |
| Turing Completeness | Lambda calculus is Turing complete and can simulate any Turing machine. | Turing machine is Turing complete; a basis for defining algorithmic computability. |
| Use in Computer Science | Foundation for functional programming languages and type theory. | Foundation of automata theory and computational complexity. |
| Operational Style | Declarative (focus on what computation is). | Procedural (focus on how computation proceeds). |
| Storage Model | No explicit memory or state; computation via substitution. | Explicit memory via tape with infinite length. |
| Significance | Basis for understanding higher-order functions and recursion. | Models algorithm execution and decidability problems. |
Expressiveness
Expressiveness in computer science refers to the ability of a programming language or computational model to represent a wide range of concepts and abstractions effectively. High expressiveness enables developers to write concise, readable, and maintainable code while capturing complex logic and structures. Languages like Python and Haskell are known for their expressiveness, supporting advanced features such as first-class functions, type inference, and pattern matching. Expressiveness directly impacts software development productivity and the ability to implement diverse algorithms efficiently.
Computational Equivalence
Computational equivalence refers to the principle that different computing systems, regardless of their architecture or programming language, can perform the same class of computations given sufficient time and resources. This concept underscores the universality of Turing machines and highlights that complex behaviors in computational systems can emerge from simple rules. Stephen Wolfram's research in cellular automata extensively explores computational equivalence, demonstrating that many seemingly simple systems exhibit computational universality. The principle has profound implications for understanding algorithmic complexity and the limits of computation in computer science.
Church-Turing Thesis
The Church-Turing Thesis defines the foundational principle of computability, stating that any function computable by an algorithm can be computed by a Turing machine or lambda calculus. This thesis bridges formal logic, computability theory, and computer science, establishing the limits of algorithmic computation. It underlies modern computer architecture and programming languages by formalizing what it means for a problem to be effectively solvable by mechanical procedures. Alan Turing's 1936 paper introduced the abstract machine model that remains central in theoretical computer science and complexity theory.
Functional vs. Imperative Paradigm
The functional programming paradigm treats computation as the evaluation of mathematical functions, avoiding changing state and mutable data. In contrast, the imperative paradigm focuses on explicit statements that change a program's state through sequences of commands. Functional languages like Haskell and Lisp emphasize immutability and higher-order functions for cleaner, more predictable code. Imperative languages such as C and Java rely on loops, variable assignments, and control structures to manage program flow and state changes.
Abstract Computation Model
The Abstract Computation Model serves as a foundational framework in computer science by formalizing how algorithms process information using abstract machines. It encompasses models such as Turing machines, lambda calculus, and finite automata, enabling rigorous analysis of computational complexity and decidability. Designed to guide algorithm development and language design, the model supports improvements in compiler construction and software verification. Research published in IEEE Computer explores these models' roles in advancing artificial intelligence and distributed computing systems.
Source and External Links
Turing Machines and Lambda Calculus Equivalence - This webpage discusses the equivalence of Turing machines and lambda calculus in terms of computational power, as established by the Church-Turing thesis.
Lambda Calculus vs. Turing Machines on Hacker News - This discussion highlights the equivalence of lambda calculus, Turing machines, and other systems of computation, while noting preferences for one over the other based on explanatory power.
l-Calculus: The Other Turing Machine - This PDF explores the history and equivalence of lambda calculus and Turing machines, emphasizing their roles in the development of the Church-Turing thesis.
FAQs
What is Lambda calculus?
Lambda calculus is a formal system in mathematical logic and computer science for expressing computation based on function abstraction and application using variable binding and substitution.
What is a Turing machine?
A Turing machine is a theoretical computational model invented by Alan Turing that manipulates symbols on an infinite tape according to a set of rules to simulate algorithmic logic and solve decision problems.
How do Lambda calculus and Turing machine differ in computation?
Lambda calculus models computation through function abstraction and application using variable substitution, while Turing machines compute via state transitions manipulating symbols on an infinite tape.
What are the basic operations of Lambda calculus?
The basic operations of Lambda calculus are: function abstraction (lx.E), function application ((E1 E2)), and variable substitution within expressions.
What problems can each model solve?
Linear regression predicts continuous numerical values, logistic regression handles binary classification tasks, decision trees classify data or predict outcomes with interpretable rules, support vector machines separate data with maximum margin for classification, neural networks model complex non-linear relationships in data, and clustering algorithms group similar data points without predefined labels.
Are Lambda calculus and Turing machines equally powerful?
Lambda calculus and Turing machines are computationally equivalent, both capable of expressing all computable functions, establishing their equal computational power.
Why are Lambda calculus and Turing machines important in computer science?
Lambda calculus and Turing machines are fundamental in computer science because they provide formal models of computation essential for understanding algorithmic processes, computability, and the limits of what can be computed.
 calledges.com
calledges.com