Monadic Bind and Applicative Functor are foundational concepts in functional programming for handling computations with effects. Monadic Bind enables sequencing of dependent computations, passing results from one function to the next, while Applicative Functors allow for combining independent computations in a context. Explore the distinct use cases and advantages of each to enhance your functional programming skills.
Main Difference
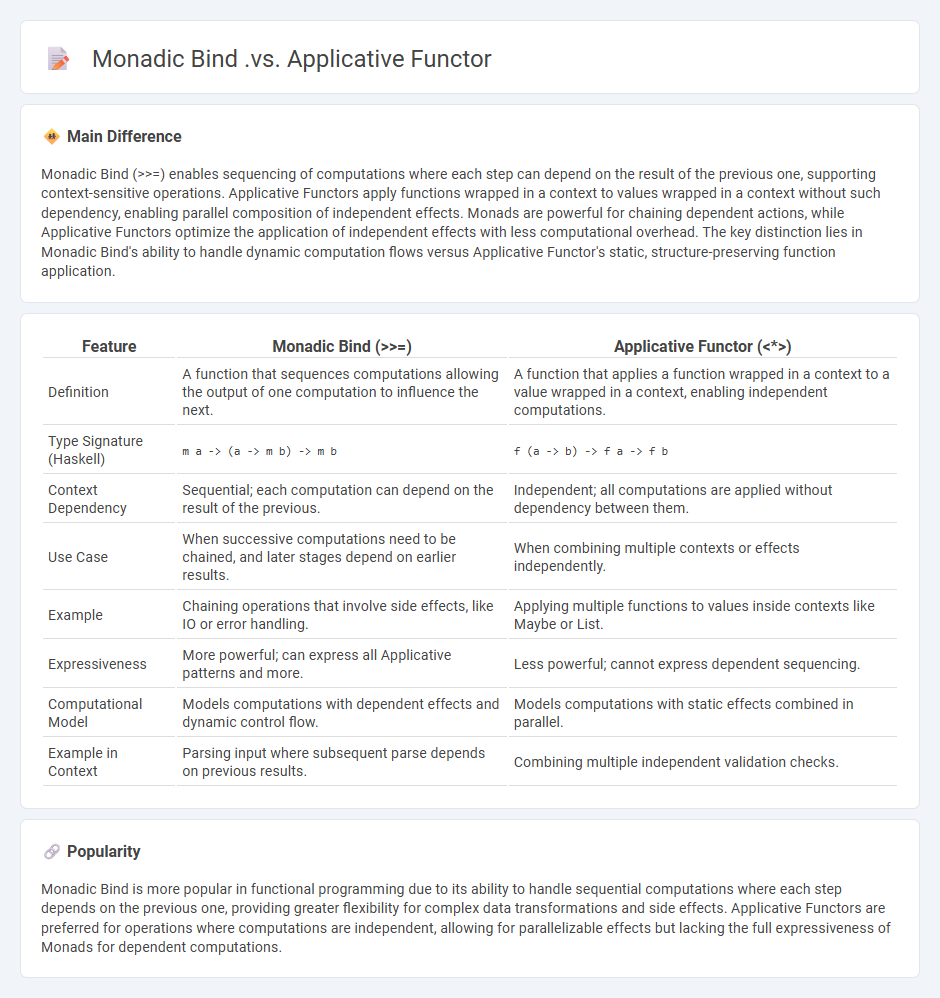
Monadic Bind (>>=) enables sequencing of computations where each step can depend on the result of the previous one, supporting context-sensitive operations. Applicative Functors apply functions wrapped in a context to values wrapped in a context without such dependency, enabling parallel composition of independent effects. Monads are powerful for chaining dependent actions, while Applicative Functors optimize the application of independent effects with less computational overhead. The key distinction lies in Monadic Bind's ability to handle dynamic computation flows versus Applicative Functor's static, structure-preserving function application.
Connection
Monadic Bind (`>>=`) extends the capabilities of Applicative Functors by enabling sequencing of operations where each step can depend on the previous result, allowing for dynamic chaining of computations. While Applicative Functors apply functions within a context independently, Monads introduce a mechanism to flatten nested contexts through the bind operation, facilitating more complex data flows. This connection is fundamental in functional programming for managing side effects and composing computations in a context-aware manner.
Comparison Table
| Feature | Monadic Bind (>>=) | Applicative Functor (<*>) |
|---|---|---|
| Definition | A function that sequences computations allowing the output of one computation to influence the next. | A function that applies a function wrapped in a context to a value wrapped in a context, enabling independent computations. |
| Type Signature (Haskell) | m a -> (a -> m b) -> m b |
f (a -> b) -> f a -> f b |
| Context Dependency | Sequential; each computation can depend on the result of the previous. | Independent; all computations are applied without dependency between them. |
| Use Case | When successive computations need to be chained, and later stages depend on earlier results. | When combining multiple contexts or effects independently. |
| Example | Chaining operations that involve side effects, like IO or error handling. | Applying multiple functions to values inside contexts like Maybe or List. |
| Expressiveness | More powerful; can express all Applicative patterns and more. | Less powerful; cannot express dependent sequencing. |
| Computational Model | Models computations with dependent effects and dynamic control flow. | Models computations with static effects combined in parallel. |
| Example in Context | Parsing input where subsequent parse depends on previous results. | Combining multiple independent validation checks. |
Sequential Composition
Sequential composition in computer science refers to the execution of multiple computational tasks one after another, ensuring that each process completes before the next begins. This concept forms the foundation of imperative programming paradigms, where statements are executed in a specific order to produce predictable outcomes. In parallel computing, sequential composition contrasts with concurrent or parallel execution models, highlighting the importance of control flow in algorithm design. Understanding sequential composition enhances debugging, program verification, and optimization techniques in software development.
Contextual Effect
Contextual effect in computer science refers to how the surrounding environment or previous interactions influence the behavior or output of a system or application. This concept is critical in user interface design, where adaptive responses improve user experience based on context like location, time, or user history. Machine learning algorithms leverage contextual effects to enhance predictive accuracy by incorporating relevant external or situational data. Understanding and implementing contextual effects enable more intuitive and personalized computing experiences.
Chaining Operations
Chaining operations in computer science refer to the process of linking multiple computational steps or functions sequentially to streamline data processing and enhance performance. This technique is widely used in programming languages like Python, JavaScript, and functional languages to create concise, readable code by passing the output of one function directly as the input to the next. Common examples include method chaining in object-oriented programming and pipeline operations in data processing frameworks such as Apache Spark. Chaining improves code modularity and reduces intermediate variables, facilitating efficient execution and easier debugging.
Applicative Lifting
Applicative lifting enhances functional programming by enabling functions to be applied over computational contexts such as functors and applicatives. This technique allows for combining multiple effects in a structured manner, improving code modularity and reusability. In Haskell, the Applicative type class implements applicative lifting through the <*> operator, facilitating effectful function application. Applicative lifting is fundamental in parsing, concurrency, and effect management within modern functional programming languages.
Computational Dependency
Computational dependency refers to the relationship between tasks or processes where one task relies on the output or completion of another to proceed. In computer systems, managing computational dependencies is crucial for optimizing parallel processing and ensuring efficient resource allocation. Techniques such as dependency graphs and scheduling algorithms help identify and resolve these dependencies in complex computations. Effective handling of computational dependencies enhances performance in applications ranging from compiler design to distributed computing environments.
Source and External Links
Functional Containers Summary: Functor vs Applicative vs Monad - This article explains the differences between Monadic Bind and Applicative Functor, highlighting that Monads allow sequential computations while Applicatives allow parallel computations.
Functors, Applicatives, And Monads In Pictures - Provides a visual explanation of how Functors, Applicatives, and Monads work, with Monadic Bind applying a function returning a wrapped value and Applicative applying a wrapped function to a wrapped value.
Functors, Applicatives, and Monads | Hacker News - Discusses the differences between Monadic Bind and Applicative Functor, noting that Monads are more dynamic with abilities like `flatMap`, while Applicatives are less dynamic but suitable for parallel computations.
FAQs
What is a monad in functional programming?
A monad in functional programming is a design pattern that encapsulates computations with context, enabling function chaining, managing side effects, and handling values like computations in a consistent, composable way.
What is an applicative functor?
An applicative functor is a type class in functional programming that allows function application lifted over a computational context, enabling the application of functions embedded in a context to values in a context.
How does monadic bind differ from applicative operations?
Monadic bind (>>=) sequences computations by passing the result of one computation to a function returning a new monadic value, enabling dependent and context-sensitive computations, whereas applicative operations (<*>, pure) combine independent computations without the need for sequencing or dependency between their results.
What are the benefits of using monadic bind?
Monadic bind enables seamless chaining of computations by handling intermediate values and context, simplifies error handling, supports composability of complex operations, and promotes clearer, more maintainable functional code.
When should you use applicative functor over monad?
Use applicative functors when effects are independent and can be evaluated in any order, improving parallelism and composability; choose monads when effects depend on previous computations and require sequential ordering.
Can all applicative functors be monads?
Not all applicative functors can be monads; every monad is an applicative functor, but some applicative functors lack the necessary bind operation to satisfy monad laws.
What are real-world examples of monadic bind and applicative functor usage?
In functional programming, monadic bind is used for chaining asynchronous API calls in JavaScript Promises, while applicative functors are utilized in validation libraries like Haskell's Validation to combine independent error checks.
 calledges.com
calledges.com