NP-complete problems are decision problems that are both in NP and as hard as any problem in NP, serving as a benchmark for computational complexity. NP-hard problems encompass a broader class, including NP-complete and other problems at least as difficult but not necessarily in NP. Explore further to understand their implications in algorithm design and computational theory.
Main Difference
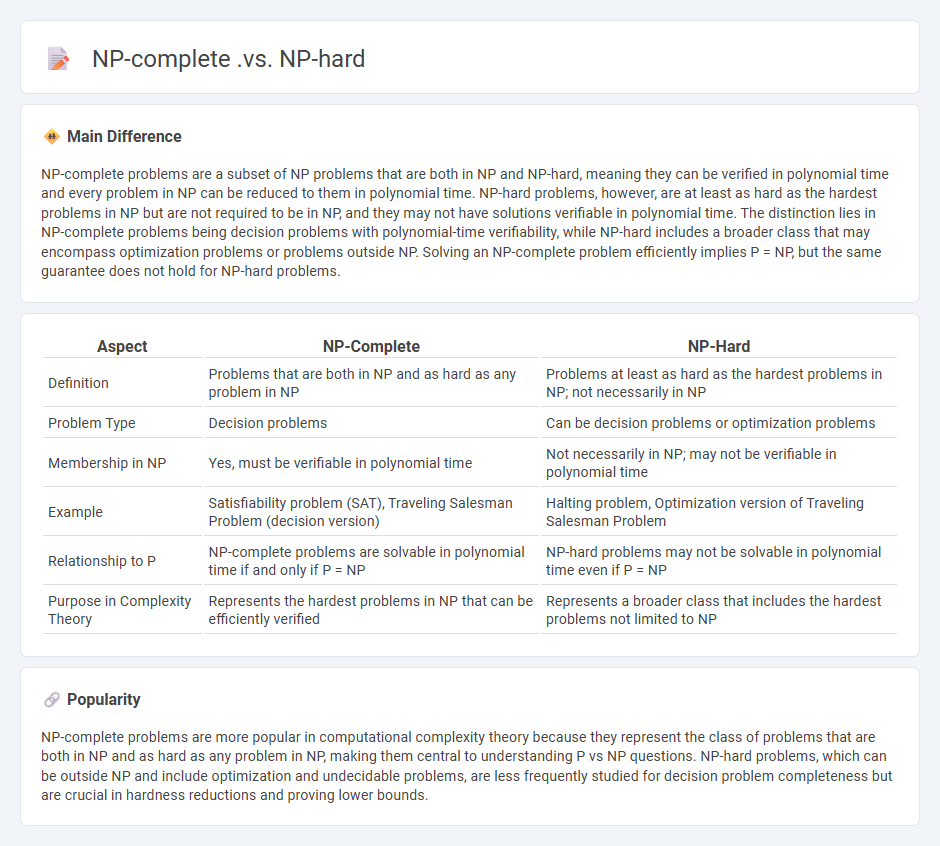
NP-complete problems are a subset of NP problems that are both in NP and NP-hard, meaning they can be verified in polynomial time and every problem in NP can be reduced to them in polynomial time. NP-hard problems, however, are at least as hard as the hardest problems in NP but are not required to be in NP, and they may not have solutions verifiable in polynomial time. The distinction lies in NP-complete problems being decision problems with polynomial-time verifiability, while NP-hard includes a broader class that may encompass optimization problems or problems outside NP. Solving an NP-complete problem efficiently implies P = NP, but the same guarantee does not hold for NP-hard problems.
Connection
NP-complete problems are a subset of NP-hard problems that are also in NP, meaning they can be verified in polynomial time. NP-hard problems include all problems at least as difficult as the hardest problems in NP, but they do not have to be in NP or be verifiable in polynomial time. The connection lies in NP-complete problems serving as the intersection where NP-hardness and membership in NP coincide, making them pivotal in computational complexity theory.
Comparison Table
| Aspect | NP-Complete | NP-Hard |
|---|---|---|
| Definition | Problems that are both in NP and as hard as any problem in NP | Problems at least as hard as the hardest problems in NP; not necessarily in NP |
| Problem Type | Decision problems | Can be decision problems or optimization problems |
| Membership in NP | Yes, must be verifiable in polynomial time | Not necessarily in NP; may not be verifiable in polynomial time |
| Example | Satisfiability problem (SAT), Traveling Salesman Problem (decision version) | Halting problem, Optimization version of Traveling Salesman Problem |
| Relationship to P | NP-complete problems are solvable in polynomial time if and only if P = NP | NP-hard problems may not be solvable in polynomial time even if P = NP |
| Purpose in Complexity Theory | Represents the hardest problems in NP that can be efficiently verified | Represents a broader class that includes the hardest problems not limited to NP |
Decision Problems
Decision problems in computer science involve determining whether a given input satisfies a specific condition or belongs to a particular set, often framed as yes/no questions. These problems are fundamental in computational complexity theory, categorizing tasks based on their solvability and resource requirements, such as time and memory. Classic examples include the Boolean satisfiability problem (SAT), which is NP-complete, and the Halting Problem, known to be undecidable. Efficiently solving or approximating decision problems impacts algorithm design, cryptography, and automated reasoning systems.
Polynomial Time Verification
Polynomial time verification refers to the process of confirming a solution to a computational problem within time complexity that scales polynomially with input size. This concept is central to the class NP (nondeterministic polynomial time), where solutions can be verified efficiently, even if finding them is potentially hard. Problems like Boolean satisfiability (SAT) exemplify polynomial time verification, as given a candidate assignment, correctness can be checked quickly. Polynomial time verification underpins foundational topics in computational complexity and algorithm design.
Reducibility
Reducibility in computer science refers to the ability to transform one computational problem into another, preserving the problem's essential characteristics. This concept is central to computational complexity theory, where problems are classified based on their relative difficulty through polynomial-time reductions. For example, the NP-completeness of the Boolean satisfiability problem (SAT) demonstrates that if SAT can be solved efficiently, then all problems in NP can be solved efficiently as well. Reducibility helps identify the boundaries between tractable and intractable problems, guiding algorithm design and complexity analysis.
Solution Existence
Solution existence in computer science refers to the determination of whether a problem has at least one valid solution within given constraints. This concept is crucial in fields such as algorithm design, computational complexity, and artificial intelligence, where algorithms must verify the feasibility of solutions before execution. For example, in NP-complete problems like the Boolean satisfiability problem (SAT), establishing solution existence guides the development of heuristic or approximate methods. Understanding solution existence enhances optimization processes and impacts decision-making in automated systems.
Computational Complexity
Computational complexity studies the resources required for algorithms to solve problems, primarily focusing on time and space. It classifies problems into complexity classes such as P, NP, and PSPACE, which help determine the feasibility of efficient computation. The concept is crucial for understanding algorithm optimization and practical limits in computer science. Research in this field guides the development of faster and more resource-efficient algorithms across various applications.
Source and External Links
Difference between NP hard and NP complete problem - This article explains the difference between NP-hard and NP-complete problems, highlighting that NP-complete problems are decision problems and a subset of NP problems, while NP-hard problems are not necessarily in NP but are at least as hard as the hardest problems in NP.
NP-completeness - This page describes NP-completeness as a property of problems that are both in NP and NP-hard, meaning they are the hardest problems in NP where solutions can be verified quickly.
P, NP, CoNP, NP hard and NP complete - This article provides an overview of various complexity classes, including NP-complete and NP-hard, explaining that NP-complete problems are both in NP and NP-hard, while NP-hard problems may not be in NP but are at least as hard as the hardest NP problems.
FAQs
What are NP-complete problems?
NP-complete problems are decision problems in computational complexity theory that are both in NP and as hard as any problem in NP, meaning every problem in NP can be reduced to them in polynomial time.
What are NP-hard problems?
NP-hard problems are computational problems as hard as the hardest problems in NP, meaning no known polynomial-time algorithm solves them, and solving one efficiently would solve all NP problems efficiently.
How do NP-complete and NP-hard problems differ?
NP-complete problems are decision problems that are both in NP and NP-hard, meaning they can be verified in polynomial time and every problem in NP can be reduced to them; NP-hard problems are at least as hard as NP-complete problems but are not required to be in NP or decision problems.
Are all NP-complete problems also NP-hard?
Yes, all NP-complete problems are NP-hard because NP-completeness requires a problem to be both in NP and NP-hard.
Is every NP-hard problem also NP-complete?
No, not every NP-hard problem is NP-complete; NP-complete problems are both NP-hard and in NP, while NP-hard problems may not belong to NP.
Why are NP-complete problems important in computer science?
NP-complete problems are important in computer science because they represent the class of the most challenging problems for which no known polynomial-time algorithms exist, and solving or efficiently approximating any NP-complete problem would lead to breakthroughs in cryptography, optimization, and complexity theory.
Can NP-hard problems be solved efficiently?
NP-hard problems cannot be solved efficiently in polynomial time unless P=NP.
 calledges.com
calledges.com