NP-Hard problems represent a class of computational challenges for which no known polynomial-time solutions exist, often serving as benchmarks for computational complexity. NP-Complete problems are a subset of NP-Hard problems characterized by their verifiability in polynomial time and equivalence in complexity to every problem in NP. Explore the nuances and implications of NP-Hard versus NP-Complete classifications to deepen your understanding of computational theory.
Main Difference
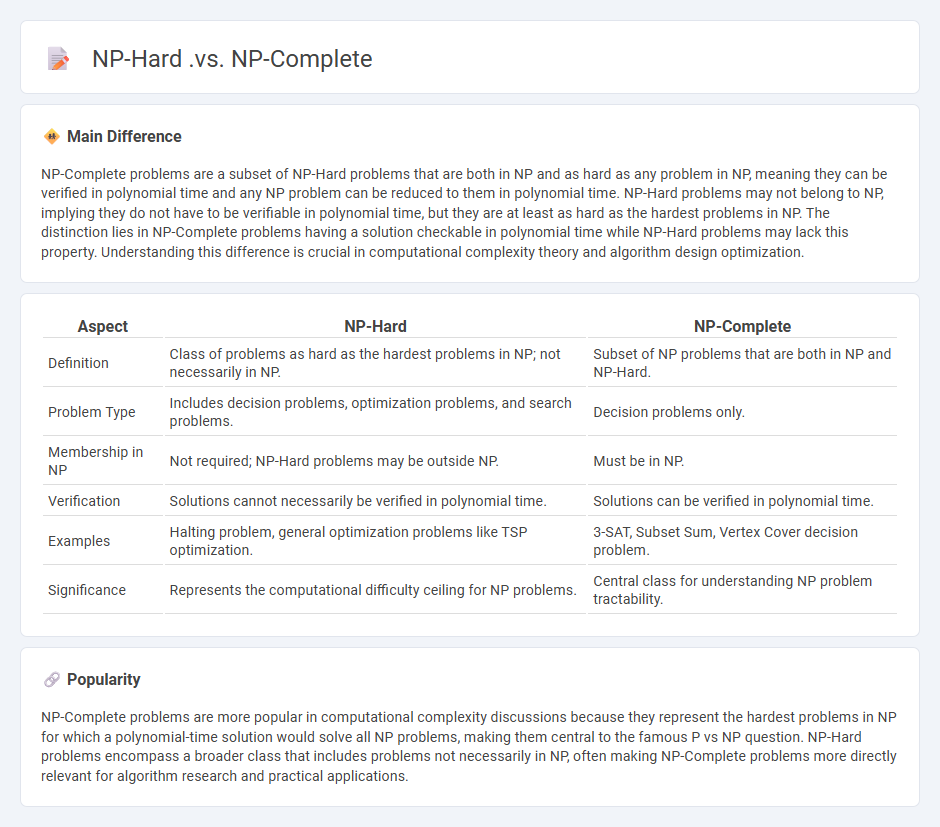
NP-Complete problems are a subset of NP-Hard problems that are both in NP and as hard as any problem in NP, meaning they can be verified in polynomial time and any NP problem can be reduced to them in polynomial time. NP-Hard problems may not belong to NP, implying they do not have to be verifiable in polynomial time, but they are at least as hard as the hardest problems in NP. The distinction lies in NP-Complete problems having a solution checkable in polynomial time while NP-Hard problems may lack this property. Understanding this difference is crucial in computational complexity theory and algorithm design optimization.
Connection
NP-Hard problems are at least as difficult as the hardest problems in NP, meaning every problem in NP can be reduced to an NP-Hard problem in polynomial time. NP-Complete problems form a subset of NP-Hard problems that are both in NP and NP-Hard, implying they can be verified and solved in nondeterministic polynomial time. Understanding the connection between NP-Hard and NP-Complete is essential for complexity theory and helps in classifying computational problems based on their tractability.
Comparison Table
| Aspect | NP-Hard | NP-Complete |
|---|---|---|
| Definition | Class of problems as hard as the hardest problems in NP; not necessarily in NP. | Subset of NP problems that are both in NP and NP-Hard. |
| Problem Type | Includes decision problems, optimization problems, and search problems. | Decision problems only. |
| Membership in NP | Not required; NP-Hard problems may be outside NP. | Must be in NP. |
| Verification | Solutions cannot necessarily be verified in polynomial time. | Solutions can be verified in polynomial time. |
| Examples | Halting problem, general optimization problems like TSP optimization. | 3-SAT, Subset Sum, Vertex Cover decision problem. |
| Significance | Represents the computational difficulty ceiling for NP problems. | Central class for understanding NP problem tractability. |
Computational Complexity
Computational complexity studies the resource requirements of algorithms, primarily focusing on time and space efficiency in solving computational problems. In computer science, complexity classes such as P, NP, and PSPACE classify problems based on their solvability and the computational effort needed. Understanding computational complexity helps optimize algorithms in fields like cryptography, artificial intelligence, and data processing. Modern research leverages complexity theory to address challenges in algorithm design and computational intractability.
Decision Problem
A decision problem in computer science is a question with a yes-or-no answer, often formulated as a formal problem to determine if an input satisfies certain conditions. It is fundamental to complexity theory and algorithm design, enabling classification of problems based on their computational difficulty, such as P, NP, or NP-complete classes. Decision problems underpin the study of automata theory, formal languages, and computability, impacting optimization and verification tasks. Recognizing a decision problem's decidability helps software engineers develop efficient algorithms and assess feasibility.
Polynomial Time
Polynomial time refers to an algorithm's computational complexity expressed as a polynomial function of the input size, typically denoted as O(n^k) for some constant k. It is a crucial concept in computer science for classifying problems based on their solvability within reasonable time frames, distinguishing between tractable problems and those considered intractable or NP-hard. Algorithms running in polynomial time are regarded as efficient and scalable, making them fundamental to fields such as algorithm design, complexity theory, and practical computing. The class P, consisting of decision problems solvable in polynomial time, serves as a benchmark for algorithmic feasibility and complexity analysis.
Verification
Verification in computer science ensures that software systems function correctly according to specifications through methods like formal verification, testing, and model checking. Formal verification employs mathematical techniques to prove program correctness, making it crucial in safety-critical domains such as aerospace and medical devices. Testing strategies, including unit testing, integration testing, and system testing, identify defects during development phases, enhancing software reliability. Model checking systematically explores state spaces of finite-state systems, detecting errors in concurrent and distributed systems effectively.
Reducibility
Reducibility in computer science refers to the ability to transform one computational problem into another, ensuring that solving the new problem effectively solves the original. This concept is fundamental in complexity theory and algorithm design, particularly in classifying problems as NP-complete or NP-hard through polynomial-time reductions. Common reducibility types include many-one reducibility and Turing reducibility, which help determine problem equivalences and computational hardness. Understanding reducibility aids in identifying the limits of efficient computation and guiding the development of algorithms.
Source and External Links
Difference between NP hard and NP complete problem - This webpage explains the distinction between NP-hard and NP-complete problems, highlighting that NP-complete problems are a subset of NP-hard but with the added requirement of being verifiable in polynomial time.
NP-completeness - Wikipedia's article on NP-completeness describes it as problems that are both in NP and NP-hard, representing the hardest problems in NP where solutions can be quickly verified.
P vs NP | What are NP-Complete and NP-Hard Problems? - This video explains the concepts of NP-complete and NP-hard problems, focusing on the relationship between these classes and the broader context of the P vs NP problem.
FAQs
What is computational complexity?
Computational complexity is the study of the amount of resources, such as time and memory, required to solve a computational problem or run an algorithm.
What defines an NP-Complete problem?
An NP-Complete problem is a decision problem that is both in NP (verifiable in polynomial time by a nondeterministic Turing machine) and NP-hard (every problem in NP can be reduced to it in polynomial time).
What defines an NP-Hard problem?
An NP-Hard problem is defined as a problem to which every problem in NP can be reduced in polynomial time, meaning it is at least as hard as the hardest problems in NP but not necessarily in NP itself.
What is the relationship between NP-Complete and NP-Hard problems?
NP-Complete problems are a subset of NP-Hard problems that are both in NP and as hard as any problem in NP, meaning every NP problem can be reduced to them in polynomial time.
Can an NP-Hard problem be unsolvable?
An NP-Hard problem is defined by its computational complexity within decision problems that are at least as hard as the hardest problems in NP, but NP-Hard does not imply undecidability; therefore, NP-Hard problems are always decidable and solvable in principle.
Are all NP-Complete problems also NP-Hard?
Yes, all NP-Complete problems are also NP-Hard because NP-Complete problems are by definition both in NP and NP-Hard.
Why are NP-Complete and NP-Hard problems important in computer science?
NP-Complete and NP-Hard problems are important in computer science because they help identify computational problems that are inherently difficult to solve efficiently, guiding algorithm design, complexity theory, and practical problem-solving strategies.
 calledges.com
calledges.com