Backward induction is a method used in game theory to solve finite sequential games by analyzing decisions from the end of the game backward to the beginning, ensuring optimal strategies at every stage. Subgame perfect equilibrium refines Nash equilibrium by requiring that players' strategies constitute a Nash equilibrium in every subgame, preventing non-credible threats. Explore deeper insights into how backward induction leads to subgame perfect equilibrium in strategic decision-making contexts.
Main Difference
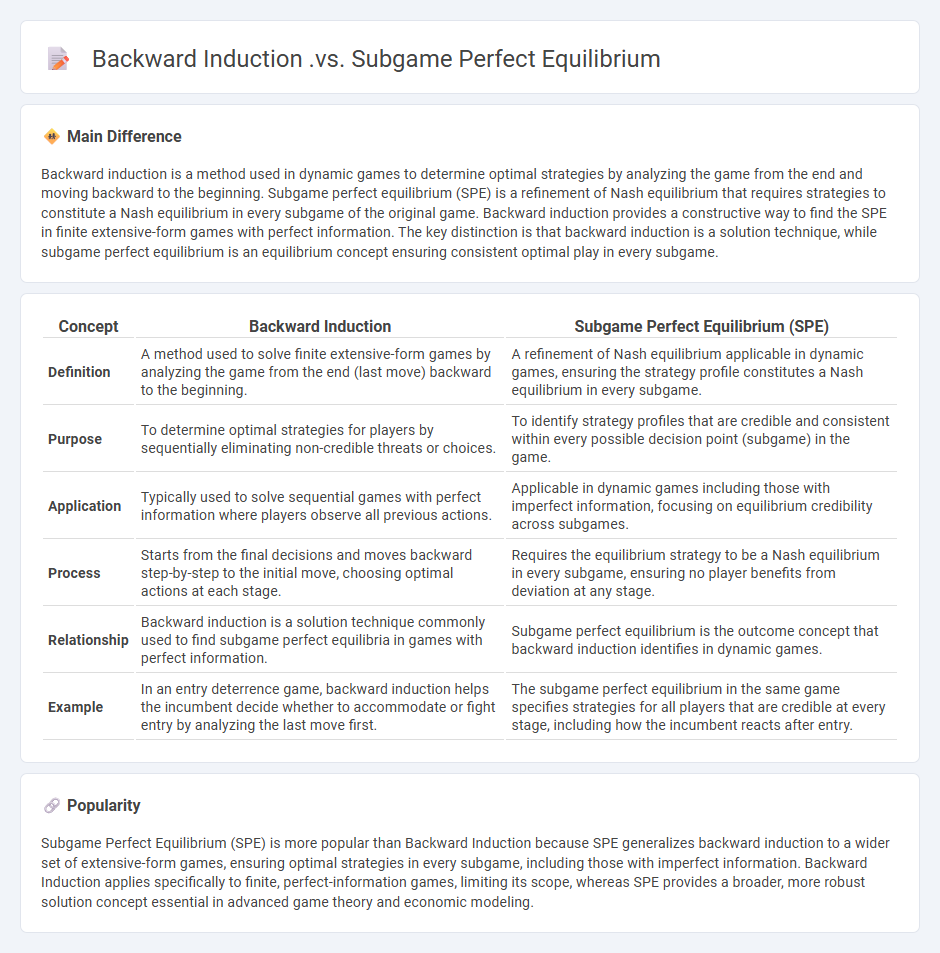
Backward induction is a method used in dynamic games to determine optimal strategies by analyzing the game from the end and moving backward to the beginning. Subgame perfect equilibrium (SPE) is a refinement of Nash equilibrium that requires strategies to constitute a Nash equilibrium in every subgame of the original game. Backward induction provides a constructive way to find the SPE in finite extensive-form games with perfect information. The key distinction is that backward induction is a solution technique, while subgame perfect equilibrium is an equilibrium concept ensuring consistent optimal play in every subgame.
Connection
Backward induction is a method used to solve extensive-form games by analyzing the game from the end and moving backward to determine optimal strategies at each decision point. Subgame perfect equilibrium is the outcome of this process, representing a strategy profile where players' actions constitute a Nash equilibrium within every subgame of the original game. The connection lies in backward induction providing the systematic approach to identify subgame perfect equilibria by ensuring credibility and optimality in sequential decision-making.
Comparison Table
| Concept | Backward Induction | Subgame Perfect Equilibrium (SPE) |
|---|---|---|
| Definition | A method used to solve finite extensive-form games by analyzing the game from the end (last move) backward to the beginning. | A refinement of Nash equilibrium applicable in dynamic games, ensuring the strategy profile constitutes a Nash equilibrium in every subgame. |
| Purpose | To determine optimal strategies for players by sequentially eliminating non-credible threats or choices. | To identify strategy profiles that are credible and consistent within every possible decision point (subgame) in the game. |
| Application | Typically used to solve sequential games with perfect information where players observe all previous actions. | Applicable in dynamic games including those with imperfect information, focusing on equilibrium credibility across subgames. |
| Process | Starts from the final decisions and moves backward step-by-step to the initial move, choosing optimal actions at each stage. | Requires the equilibrium strategy to be a Nash equilibrium in every subgame, ensuring no player benefits from deviation at any stage. |
| Relationship | Backward induction is a solution technique commonly used to find subgame perfect equilibria in games with perfect information. | Subgame perfect equilibrium is the outcome concept that backward induction identifies in dynamic games. |
| Example | In an entry deterrence game, backward induction helps the incumbent decide whether to accommodate or fight entry by analyzing the last move first. | The subgame perfect equilibrium in the same game specifies strategies for all players that are credible at every stage, including how the incumbent reacts after entry. |
Sequential Games
Sequential games in economics model strategic interactions where players make decisions one after another, with each player observing previous actions before choosing their strategy. These games are analyzed using backward induction to find subgame perfect equilibria, ensuring credibility in players' strategies throughout the game. Important applications include auction design, bargaining models, and oligopoly market competition, where timing and order of moves significantly affect outcomes. Key researchers like Reinhard Selten and David Kreps have contributed to formalizing solution concepts in sequential decision-making scenarios.
Nash Equilibrium
Nash Equilibrium represents a fundamental concept in game theory where each player's strategy is optimal, given the strategies of all other players, resulting in no incentive to deviate unilaterally. In economics, this equilibrium helps predict outcomes in competitive markets, auctions, oligopolies, and bargaining scenarios. Real-world applications include firms setting prices in a duopoly or countries in trade negotiations, where strategic interdependence shapes decisions. John Nash formalized this concept in the 1950s, earning a Nobel Prize in Economic Sciences in 1994 for his contribution.
Perfect Information
Perfect information in economics refers to a market condition where all consumers and producers have complete and instantaneous knowledge about prices, product quality, and availability. This concept underpins models of perfect competition, ensuring no participant can gain an advantage through asymmetric information. Real-world examples include agricultural markets where prices and product attributes are publicly accessible. The assumption of perfect information helps economists analyze market efficiency and the implications of information asymmetry on economic welfare.
Subgames
Subgames represent distinct segments within a larger game, each beginning at a specific decision node and encompassing all subsequent actions and outcomes. Subgame perfection refines Nash equilibrium by requiring strategies to constitute a Nash equilibrium in every subgame, ensuring credible and consistent decision-making throughout. This concept, formalized by Reinhard Selten in 1965, plays a critical role in dynamic game analysis and sequential equilibrium refinement. It allows economists to analyze strategic interactions where future decisions depend on earlier moves, improving predictive accuracy in economic modeling.
Credible Strategies
Credible strategies in economics refer to commitment mechanisms that ensure agents follow through on announced plans in game-theoretic scenarios, enhancing predictability and stability in markets. These strategies are essential in repeated games where player incentives depend on trust and reputation, often modeled through subgame perfect equilibrium. Central banks, for instance, employ credible monetary policies to anchor inflation expectations and influence long-term interest rates effectively. Empirical studies confirm that transparent communication and consistent policy actions increase the credibility of economic agents, reducing uncertainty and promoting investment.
Source and External Links
Subgame perfect equilibrium (Wikipedia) - Backward induction is a common method to find subgame perfect equilibria (SPE) in finite games by analyzing optimal strategies starting from the end of the game, but SPE is a more general equilibrium concept that rules out non-credible threats and applies to all subgames of the game.
Backward induction and subgame perfection (PDF) - Backward induction solves games by reasoning from the last stage backwards and all backward induction solutions are Nash equilibria, but they represent special cases of the more general subgame perfect equilibria concept, which refines Nash equilibria to eliminate non-credible threats.
Theory: subgame perfect equilibrium (UGA PDF) - In games with perfect information and finite actions, backward induction exactly identifies the set of subgame perfect equilibria, making backward induction both a solution technique and a way to characterize SPE in such games.
FAQs
What is backward induction?
Backward induction is a method used in game theory to solve finite sequential games by analyzing the game from the end to the beginning to determine optimal strategies.
What is subgame perfect equilibrium?
Subgame perfect equilibrium is a refinement of Nash equilibrium where players' strategies constitute a Nash equilibrium in every subgame of the original game, ensuring credibility of threats and promises throughout the game.
How does backward induction relate to subgame perfect equilibrium?
Backward induction is a method used to find the subgame perfect equilibrium by solving the game from the end backward, ensuring optimal strategies in every subgame.
When should backward induction be used?
Backward induction should be used when analyzing finite sequential games with perfect information to determine optimal strategies by reasoning backward from the end of the game.
Can every subgame perfect equilibrium be found using backward induction?
Every subgame perfect equilibrium in a finite extensive-form game with perfect information can be found using backward induction.
What types of games use subgame perfect equilibrium?
Subgame perfect equilibrium is used in extensive-form games with sequential moves, including bargaining games, dynamic pricing games, entry deterrence games, and repeated games with observable actions.
Why are these concepts important in game theory?
These concepts are important in game theory because they provide frameworks for predicting players' strategic interactions, ensuring equilibrium stability, optimizing decision-making, and understanding competitive behaviors in various economic and social scenarios.
 calledges.com
calledges.com