Samuelson condition defines optimal public goods provision by equating the sum of individual marginal rates of substitution to the marginal cost, ensuring efficiency in resource allocation. Lindahl equilibrium achieves this efficiency through personalized prices reflecting each individual's valuation of the public good, balancing demand and supply in a decentralized manner. Explore how these concepts shape public economics and guide policy design.
Main Difference
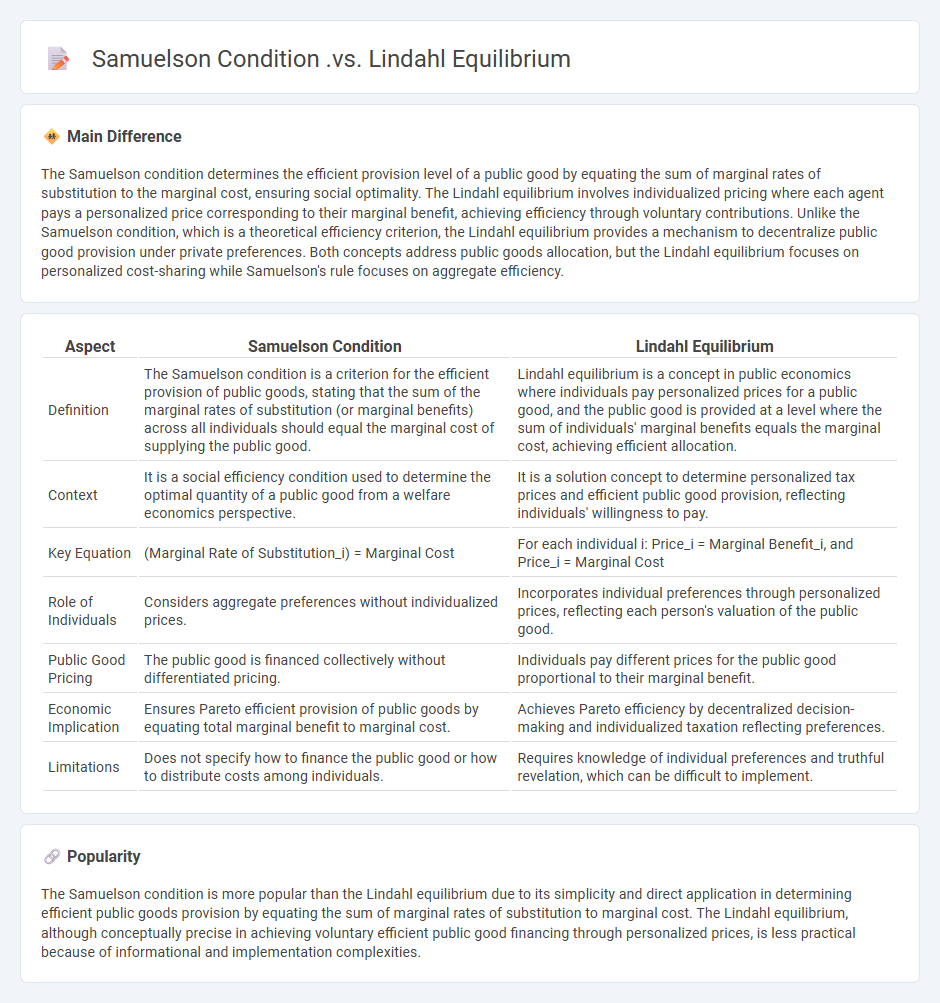
The Samuelson condition determines the efficient provision level of a public good by equating the sum of marginal rates of substitution to the marginal cost, ensuring social optimality. The Lindahl equilibrium involves individualized pricing where each agent pays a personalized price corresponding to their marginal benefit, achieving efficiency through voluntary contributions. Unlike the Samuelson condition, which is a theoretical efficiency criterion, the Lindahl equilibrium provides a mechanism to decentralize public good provision under private preferences. Both concepts address public goods allocation, but the Lindahl equilibrium focuses on personalized cost-sharing while Samuelson's rule focuses on aggregate efficiency.
Connection
The Samuelson condition defines the efficient provision level for public goods by equating the sum of marginal rates of substitution to the marginal cost, ensuring Pareto optimality. Lindahl equilibrium builds on this by assigning personalized prices to individuals reflecting their marginal valuations, achieving an outcome where public goods provision meets the Samuelson condition. Both concepts are fundamental in public economics for resolving the free-rider problem and determining optimal public goods financing through individualized marginal benefit sharing.
Comparison Table
| Aspect | Samuelson Condition | Lindahl Equilibrium |
|---|---|---|
| Definition | The Samuelson condition is a criterion for the efficient provision of public goods, stating that the sum of the marginal rates of substitution (or marginal benefits) across all individuals should equal the marginal cost of supplying the public good. | Lindahl equilibrium is a concept in public economics where individuals pay personalized prices for a public good, and the public good is provided at a level where the sum of individuals' marginal benefits equals the marginal cost, achieving efficient allocation. |
| Context | It is a social efficiency condition used to determine the optimal quantity of a public good from a welfare economics perspective. | It is a solution concept to determine personalized tax prices and efficient public good provision, reflecting individuals' willingness to pay. |
| Key Equation | (Marginal Rate of Substitution_i) = Marginal Cost | For each individual i: Price_i = Marginal Benefit_i, and Price_i = Marginal Cost |
| Role of Individuals | Considers aggregate preferences without individualized prices. | Incorporates individual preferences through personalized prices, reflecting each person's valuation of the public good. |
| Public Good Pricing | The public good is financed collectively without differentiated pricing. | Individuals pay different prices for the public good proportional to their marginal benefit. |
| Economic Implication | Ensures Pareto efficient provision of public goods by equating total marginal benefit to marginal cost. | Achieves Pareto efficiency by decentralized decision-making and individualized taxation reflecting preferences. |
| Limitations | Does not specify how to finance the public good or how to distribute costs among individuals. | Requires knowledge of individual preferences and truthful revelation, which can be difficult to implement. |
Public Goods
Public goods are economic commodities characterized by non-excludability and non-rivalry, meaning individuals cannot be effectively excluded from use and one person's consumption does not reduce availability to others. Examples include national defense, public parks, and clean air, which are often underprovided by private markets due to free-rider problems. Governments typically supply public goods through taxation and public funding to ensure efficient provision. Economic theories such as Samuelson's rule analyze optimal public goods provision based on aggregate marginal cost and benefit.
Marginal Rate of Substitution
The Marginal Rate of Substitution (MRS) measures the rate at which a consumer is willing to exchange one good for another while maintaining the same level of utility. It is calculated as the negative slope of an indifference curve, represented mathematically by the ratio of the marginal utilities of the two goods. Understanding MRS is crucial for analyzing consumer choice behavior and optimization under budget constraints. Empirical studies often use MRS to assess preferences and substitution effects between products in microeconomic models.
Individual vs. Collective Demand
Individual demand represents the quantity of a good or service a single consumer is willing and able to purchase at various price levels. Collective demand, or market demand, aggregates the individual demands of all consumers within a market for a specific product. Market demand curves are derived by horizontally summing individual demand curves, indicating total quantity demanded at each price point. Understanding the distinction helps analyze consumer behavior and forecast changes in economic markets.
Efficient Provision
Efficient provision in economics refers to allocating resources in a manner that maximizes total social welfare without waste. It involves optimizing production and distribution processes so that goods or services are supplied at the lowest possible cost while meeting consumer demand. Market mechanisms, such as competitive pricing, often guide efficient provision by balancing supply and demand. Public goods and externalities present challenges, requiring government intervention to achieve efficiency.
Personalized Pricing
Personalized pricing refers to the strategy where sellers set different prices for the same product or service based on individual consumer data, such as purchasing behavior, demographics, or willingness to pay. Advanced data analytics and machine learning algorithms enable firms to segment markets and tailor prices, enhancing revenue and profit margins. In economics, personalized pricing challenges traditional uniform pricing models by exploiting consumer surplus and increasing market efficiency. The approach raises ethical and regulatory concerns related to privacy, fairness, and potential discrimination in competitive markets.
Source and External Links
Samuelson condition - The Samuelson condition specifies the optimal provision rule for public goods, requiring that the sum of individuals' marginal rates of substitution (their willingness to pay) equals the economy-wide marginal rate of transformation (cost of provision), ensuring efficient public good supply.
Econ 2230: Public Economics - Lindahl Equilibrium - The Lindahl equilibrium is a concept where individuals pay personalized prices for a public good such that their combined demand and payments lead to an efficient and Pareto optimal provision that satisfies the Samuelson condition, effectively internalizing public good externalities.
Lecture Notes: Public Economics - The Samuelson condition provides a normative criterion for efficiency in public goods provision, while the Lindahl equilibrium is a theoretical construct where individuals reveal their true marginal valuations and pay personalized prices supporting that efficient outcome, thus linking individual incentives to the Samuelson rule.
FAQs
What is the Samuelson condition?
The Samuelson condition states that the efficient provision of a public good occurs when the sum of the marginal rates of substitution (individuals' marginal benefits) equals the marginal cost of providing the good.
What is Lindahl equilibrium?
Lindahl equilibrium is a concept in public economics where individuals pay personalized prices for public goods, ensuring efficient provision and fair cost-sharing based on their marginal benefits.
How does the Samuelson condition determine efficient public good provision?
The Samuelson condition determines efficient public good provision by equating the sum of all individuals' marginal rates of substitution between the public good and a private good to the marginal cost of providing one more unit of the public good.
How is Lindahl equilibrium used to allocate costs for public goods?
Lindahl equilibrium allocates public good costs by assigning personalized prices to individuals based on their marginal valuation, ensuring each person's payment equals their perceived benefit, leading to efficient and equitable cost-sharing.
What are the main differences between Samuelson condition and Lindahl equilibrium?
The Samuelson condition states that the sum of the marginal rates of substitution equals the marginal cost of public goods provision, ensuring efficient public goods provision, while the Lindahl equilibrium achieves efficiency by assigning personalized prices to individuals based on their marginal valuations, leading to voluntary contributions that finance the public good without free-riding.
Why is the Samuelson condition important in welfare economics?
The Samuelson condition is important in welfare economics because it provides the efficient provision rule for public goods, ensuring that the sum of marginal rates of substitution equals the marginal cost of provision, maximizing social welfare.
How do Lindahl prices relate to individual willingness to pay for public goods?
Lindahl prices equal each individual's marginal willingness to pay for the public good, aligning personalized prices so that the sum finances the efficient provision level.
 calledges.com
calledges.com