Nash equilibrium and subgame perfect equilibrium are key solution concepts in game theory that analyze strategic interactions among rational players. Nash equilibrium occurs when no player can improve their payoff by unilaterally changing their strategy, while subgame perfect equilibrium refines this by requiring strategies to constitute a Nash equilibrium in every subgame of the original game. Explore the distinctions and applications of these equilibria to deepen your understanding of strategic decision-making.
Main Difference
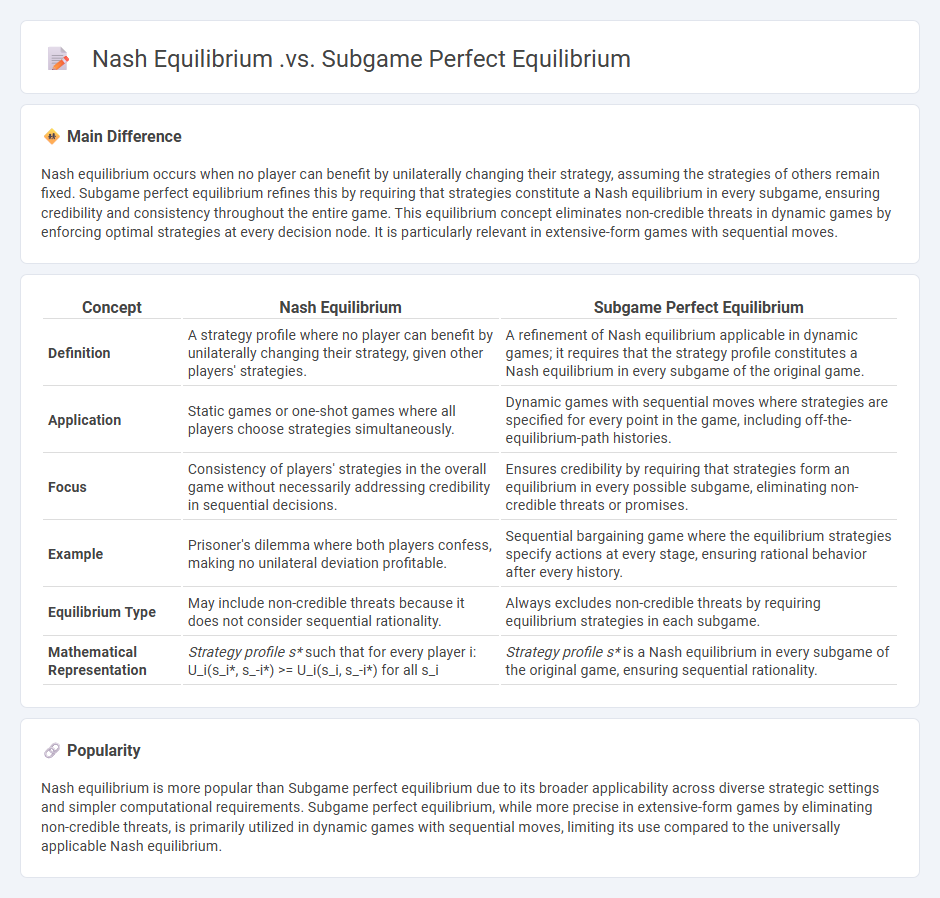
Nash equilibrium occurs when no player can benefit by unilaterally changing their strategy, assuming the strategies of others remain fixed. Subgame perfect equilibrium refines this by requiring that strategies constitute a Nash equilibrium in every subgame, ensuring credibility and consistency throughout the entire game. This equilibrium concept eliminates non-credible threats in dynamic games by enforcing optimal strategies at every decision node. It is particularly relevant in extensive-form games with sequential moves.
Connection
Nash equilibrium represents a strategy profile where no player benefits from unilaterally deviating, ensuring mutual best responses in the entire game. Subgame perfect equilibrium refines this concept by requiring that strategies form a Nash equilibrium in every subgame, eliminating non-credible threats. This connection strengthens strategic consistency throughout dynamic games, making subgame perfect equilibrium a more precise solution concept in extensive-form games.
Comparison Table
| Concept | Nash Equilibrium | Subgame Perfect Equilibrium |
|---|---|---|
| Definition | A strategy profile where no player can benefit by unilaterally changing their strategy, given other players' strategies. | A refinement of Nash equilibrium applicable in dynamic games; it requires that the strategy profile constitutes a Nash equilibrium in every subgame of the original game. |
| Application | Static games or one-shot games where all players choose strategies simultaneously. | Dynamic games with sequential moves where strategies are specified for every point in the game, including off-the-equilibrium-path histories. |
| Focus | Consistency of players' strategies in the overall game without necessarily addressing credibility in sequential decisions. | Ensures credibility by requiring that strategies form an equilibrium in every possible subgame, eliminating non-credible threats or promises. |
| Example | Prisoner's dilemma where both players confess, making no unilateral deviation profitable. | Sequential bargaining game where the equilibrium strategies specify actions at every stage, ensuring rational behavior after every history. |
| Equilibrium Type | May include non-credible threats because it does not consider sequential rationality. | Always excludes non-credible threats by requiring equilibrium strategies in each subgame. |
| Mathematical Representation |
Strategy profile s* such that for every player i: U_i(s_i*, s_-i*) >= U_i(s_i, s_-i*) for all s_i |
Strategy profile s* is a Nash equilibrium in every subgame of the original game, ensuring sequential rationality. |
Strategy Profile
A strategy profile in economics refers to a comprehensive set of strategies chosen by all players in a game, defining the actions each participant will take. It is fundamental in game theory, where analyzing these profiles helps predict outcomes in competitive situations like markets or auctions. Each strategy profile corresponds to a specific combination of choices across players, influencing payoffs and equilibrium states such as the Nash equilibrium. Understanding strategy profiles enables economists to model decision-making processes in oligopolies, bargaining, and public goods provision.
Credibility
Credibility in economics refers to the trustworthiness and reliability of policymakers, especially central banks, in maintaining consistent and transparent monetary policies to achieve targeted inflation and economic stability. It influences inflation expectations, which directly affect wage-setting behavior and investment decisions, thereby impacting overall economic performance. Empirical studies show that countries with high central bank credibility experience lower inflation volatility and more stable economic growth. This concept is central to the effectiveness of rules-based policies and commitment mechanisms in macroeconomic frameworks.
Sequential Rationality
Sequential rationality is a key concept in game theory and economics that ensures players make optimal decisions at every stage of a dynamic game, considering the history of actions taken so far. This principle refines the equilibrium concept by requiring that strategies form a Nash equilibrium in every subgame, promoting consistent and credible decision-making. Applied extensively in dynamic games, sequential rationality informs models of extensive-form games, auction theory, and dynamic pricing strategies. Empirical research often uses sequential rationality to analyze bargaining scenarios and market competition, enhancing predictions of strategic behavior over time.
Non-cooperative Games
Non-cooperative games in economics analyze strategic interactions where players make decisions independently without binding agreements. These games model competitive market behavior, oligopoly pricing, and auctions, emphasizing equilibrium concepts such as Nash equilibrium. John Nash's work in the 1950s provided foundational tools for predicting outcomes where each participant maximizes their utility given others' strategies. Applications extend to contract theory, bargaining scenarios, and environmental economics, influencing policy design and industrial organization.
Backward Induction
Backward induction is a fundamental method in economics and game theory for solving sequential games by analyzing the game from the end to the beginning. It involves anticipating future actions and payoffs to determine optimal strategies at each decision node, ensuring rational behavior in dynamic settings. This technique is widely applied in scenarios such as bargaining, auctions, and oligopoly models, providing insights into subgame perfect equilibrium outcomes. Nobel laureate Reinhard Selten formalized backward induction as a key concept in non-cooperative game theory during the 1970s.
Source and External Links
Subgame perfect equilibrium - Wikipedia - A subgame perfect equilibrium (SPE) is a refinement of Nash equilibrium where the strategy constitutes a Nash equilibrium in every subgame, ensuring credibility of strategies through backward induction, while Nash equilibria that fail this condition may not be subgame perfect.
Chapter 11 Subgame-Perfect Nash Equilibrium - MIT OpenCourseWare - Every subgame perfect equilibrium is a Nash equilibrium but not all Nash equilibria are subgame perfect; SPEs are found by backwards induction, verifying that strategies form Nash equilibria in every subgame, thus eliminating non-credible threats.
Theory: Subgame Perfect Equilibrium - University of Georgia - Subgame perfect equilibrium requires that players' strategies form Nash equilibria in every subgame, refining Nash equilibrium by imposing credibility conditions and typically identified via backward induction, distinguishing it from non-credible Nash equilibria.
FAQs
What is Nash equilibrium?
Nash equilibrium is a game theory concept where no player can benefit by changing their strategy while other players keep theirs unchanged.
What is subgame perfect equilibrium?
Subgame perfect equilibrium is a refinement of Nash equilibrium where strategies constitute a Nash equilibrium in every subgame of the original game, ensuring credible and consistent optimal decisions at every stage.
How do Nash equilibrium and subgame perfect equilibrium differ?
Nash equilibrium is a strategy profile where no player can gain by unilaterally changing their strategy, while subgame perfect equilibrium refines this by requiring strategies to form a Nash equilibrium in every subgame, ensuring credibility and consistency in dynamic games.
Why is subgame perfect equilibrium considered a refinement of Nash equilibrium?
Subgame perfect equilibrium is considered a refinement of Nash equilibrium because it requires strategies to constitute a Nash equilibrium in every subgame, eliminating non-credible threats and ensuring consistent optimal play throughout the entire game tree.
What types of games require subgame perfect equilibrium?
Games with sequential moves and perfect information, such as extensive-form games, require subgame perfect equilibrium for credible strategy analysis.
Can every Nash equilibrium be a subgame perfect equilibrium?
No, not every Nash equilibrium is a subgame perfect equilibrium; only those Nash equilibria that induce Nash equilibria in every subgame qualify as subgame perfect equilibria.
Why is subgame perfect equilibrium important in game theory?
Subgame perfect equilibrium ensures strategy credibility by requiring optimal actions in every subgame, eliminating non-credible threats and enabling accurate prediction of outcomes in dynamic games.
 calledges.com
calledges.com