Arrow-Debreu Equilibrium and Walrasian Equilibrium both describe market states where supply meets demand across all goods and services, ensuring no participant has an incentive to change their behavior. The Arrow-Debreu model incorporates uncertainty and a complete set of contingent commodities, offering a more generalized and mathematically rigorous framework. Explore the differences and applications of these equilibrium concepts to deepen your understanding of economic theory.
Main Difference
Arrow-Debreu Equilibrium generalizes the Walrasian Equilibrium by incorporating a complete set of state-contingent securities to handle uncertainty and time, ensuring optimal allocation across all possible states of the world. Walrasian Equilibrium focuses on price vectors and allocation in a static framework without explicitly modeling uncertainty or future contingencies. Both concepts rely on market-clearing conditions and rational agents maximizing utility or profit. Arrow-Debreu's framework is fundamental in financial economics for modeling contingent claims markets, whereas Walrasian Equilibrium is a cornerstone of classical general equilibrium theory.
Connection
Arrow-Debreu Equilibrium generalizes Walrasian Equilibrium by incorporating uncertainty and contingent commodities into the market model. Both concepts rely on price systems to clear markets and achieve Pareto efficiency among agents with convex preferences. Arrow-Debreu's framework extends Walrasian Equilibrium by proving existence under more general conditions, including complete markets and state-contingent claims.
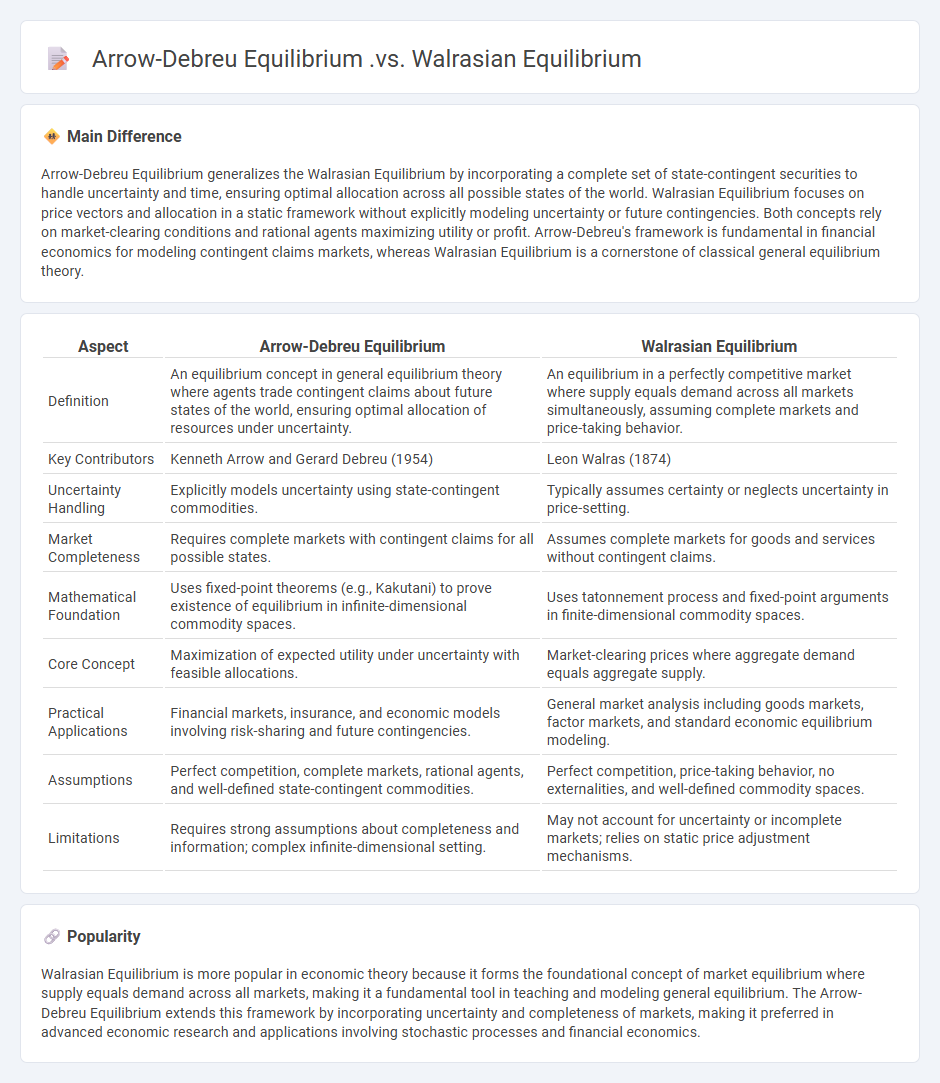
Comparison Table
| Aspect | Arrow-Debreu Equilibrium | Walrasian Equilibrium |
|---|---|---|
| Definition | An equilibrium concept in general equilibrium theory where agents trade contingent claims about future states of the world, ensuring optimal allocation of resources under uncertainty. | An equilibrium in a perfectly competitive market where supply equals demand across all markets simultaneously, assuming complete markets and price-taking behavior. |
| Key Contributors | Kenneth Arrow and Gerard Debreu (1954) | Leon Walras (1874) |
| Uncertainty Handling | Explicitly models uncertainty using state-contingent commodities. | Typically assumes certainty or neglects uncertainty in price-setting. |
| Market Completeness | Requires complete markets with contingent claims for all possible states. | Assumes complete markets for goods and services without contingent claims. |
| Mathematical Foundation | Uses fixed-point theorems (e.g., Kakutani) to prove existence of equilibrium in infinite-dimensional commodity spaces. | Uses tatonnement process and fixed-point arguments in finite-dimensional commodity spaces. |
| Core Concept | Maximization of expected utility under uncertainty with feasible allocations. | Market-clearing prices where aggregate demand equals aggregate supply. |
| Practical Applications | Financial markets, insurance, and economic models involving risk-sharing and future contingencies. | General market analysis including goods markets, factor markets, and standard economic equilibrium modeling. |
| Assumptions | Perfect competition, complete markets, rational agents, and well-defined state-contingent commodities. | Perfect competition, price-taking behavior, no externalities, and well-defined commodity spaces. |
| Limitations | Requires strong assumptions about completeness and information; complex infinite-dimensional setting. | May not account for uncertainty or incomplete markets; relies on static price adjustment mechanisms. |
Complete Markets
Complete markets refer to a theoretical economic framework where every conceivable risk can be traded through financial instruments, ensuring perfect risk-sharing among agents. In such markets, for every possible future state of the world, there exists a corresponding asset or security whose payoff depends precisely on that state, eliminating uncertainty. Complete markets facilitate efficient allocation of resources and optimal consumption-smoothing across different states and time periods. This concept underpins fundamental models in general equilibrium theory and asset pricing, such as the Arrow-Debreu model.
State-Contingent Commodities
State-contingent commodities refer to goods whose delivery depends on the realization of specific states of the world, allowing for more precise risk-sharing in uncertain economic environments. These commodities are contracts that pay off only if particular future conditions or events occur, effectively linking consumption or production to contingent states. In economics, state-contingent claims facilitate efficient allocation of resources and enable agents to hedge against uncertainty by trading based on possible future states. This concept plays a crucial role in general equilibrium theory and financial economics, underpinning market completeness and the design of optimal insurance mechanisms.
Existence Theorem
The Existence Theorem in economics guarantees that under certain conditions, such as continuity, compactness, and convexity of preferences and production sets, an equilibrium exists in a market or game. John Nash's Existence Theorem specifically proves that every finite game with mixed strategies has at least one Nash equilibrium. Fixed-point theorems, like Brouwer or Kakutani, often underpin these proofs, ensuring solutions in competitive or non-cooperative environments. This foundational result supports the analysis of market stability, resource allocation, and strategic behavior in microeconomics.
Time and Uncertainty
Time profoundly influences economic decision-making by affecting investment horizons, consumption choices, and risk assessment. Uncertainty in economics arises from unpredictable factors like market fluctuations, policy changes, and technological innovations, shaping agents' expectations and behavior. Models such as the Expected Utility Theory and Real Options Analysis incorporate time and uncertainty to better predict economic outcomes. Empirical studies demonstrate that higher uncertainty often leads to reduced investment and slower economic growth, highlighting the critical role these factors play in macroeconomic stability.
Market Clearing
Market clearing in economics refers to the equilibrium state where the quantity of goods supplied equals the quantity demanded, resulting in no excess supply or shortage. Prices adjust dynamically to reach this point, ensuring that every unit produced is sold without surplus inventory. Market clearing is fundamental in classical and neoclassical economic models, facilitating efficient resource allocation. This concept underpins auction designs, stock market transactions, and commodity exchanges worldwide.
Source and External Links
Arrow-Debreu Model - The Arrow-Debreu model is a formalized Walrasian economic equilibrium system that proves the existence of competitive equilibrium in a perfectly competitive market.
Arrow-Debreu Economy - The Arrow-Debreu economy is characterized by a complete set of markets for goods and services, equating supply and demand at equilibrium prices.
Walrasian Equilibrium - The Walrasian equilibrium is a theoretical model where markets clear through a process of auctioneering, ensuring that supply equals demand at the equilibrium price.
FAQs
What is a general equilibrium in economics?
General equilibrium in economics is a state where supply and demand balance simultaneously across all markets, ensuring that all prices and quantities are mutually consistent and no excess supply or demand exists.
What defines an Arrow-Debreu equilibrium?
An Arrow-Debreu equilibrium is defined by a price system and an allocation of goods where every consumer maximizes utility given their budget constraint, every producer maximizes profit, and all markets clear simultaneously.
What defines a Walrasian equilibrium?
A Walrasian equilibrium is defined as a state in an economy where supply equals demand across all markets simultaneously, and all agents optimize their utility or profit given prices, with a price vector that clears the markets.
How do Arrow-Debreu and Walrasian models handle goods and markets?
Arrow-Debreu models represent goods as state-contingent commodities traded in complete markets at equilibrium prices, while Walrasian models treat goods as homogeneous commodities exchanged in perfectly competitive markets with prices adjusting to clear supply and demand.
What mathematical assumptions are unique to the Arrow-Debreu framework?
Arrow-Debreu framework uniquely assumes complete markets with a state-contingent commodity space represented by continuous, bounded, measurable functions, agents having convex, closed, and complete preference relations satisfying continuity and monotonicity, perfectly competitive markets ensuring price-taking behavior, and the existence of a numeraire enabling normalized price vectors within a compact, convex price simplex.
How do the concepts of time and uncertainty differ in both equilibria?
In static equilibrium, time is absent and uncertainty is minimal as all variables are fixed; in dynamic equilibrium, time plays a crucial role with changing variables and inherent uncertainty due to evolving conditions and future expectations.
Why are Arrow-Debreu and Walrasian equilibria important in economic theory?
Arrow-Debreu and Walrasian equilibria are important in economic theory because they guarantee the existence of a price system where supply equals demand across all markets, enabling efficient resource allocation and serving as foundational models for general equilibrium analysis.
 calledges.com
calledges.com