The Laffer Curve illustrates the relationship between tax rates and tax revenue, highlighting an optimal tax rate that maximizes government income without discouraging productivity. The Haavelmo Theorem, grounded in Keynesian economics, asserts that government spending boosts overall demand and income without increasing taxes or debt under certain conditions. Explore these foundational economic concepts to understand their impacts on fiscal policy and economic growth.
Main Difference
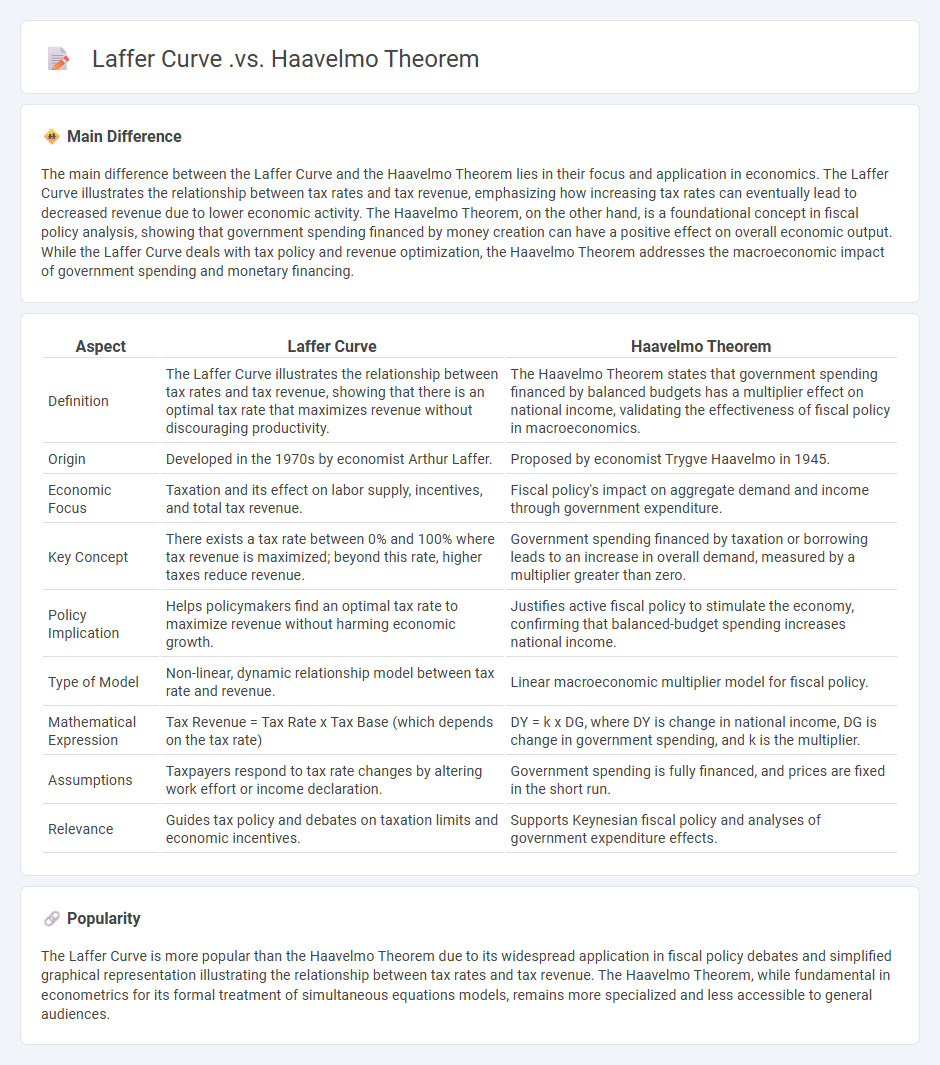
The main difference between the Laffer Curve and the Haavelmo Theorem lies in their focus and application in economics. The Laffer Curve illustrates the relationship between tax rates and tax revenue, emphasizing how increasing tax rates can eventually lead to decreased revenue due to lower economic activity. The Haavelmo Theorem, on the other hand, is a foundational concept in fiscal policy analysis, showing that government spending financed by money creation can have a positive effect on overall economic output. While the Laffer Curve deals with tax policy and revenue optimization, the Haavelmo Theorem addresses the macroeconomic impact of government spending and monetary financing.
Connection
The Laffer Curve illustrates the relationship between tax rates and tax revenue, showing that beyond a certain point, higher taxes reduce total revenue. Haavelmo's Theorem underlines the importance of government spending financed by taxes in influencing aggregate demand and economic output. Their connection lies in balancing taxation and public expenditure to optimize fiscal policy, where the Laffer Curve informs the efficient tax rate, and Haavelmo's Theorem supports the multiplier effect of government spending on economic growth.
Comparison Table
| Aspect | Laffer Curve | Haavelmo Theorem |
|---|---|---|
| Definition | The Laffer Curve illustrates the relationship between tax rates and tax revenue, showing that there is an optimal tax rate that maximizes revenue without discouraging productivity. | The Haavelmo Theorem states that government spending financed by balanced budgets has a multiplier effect on national income, validating the effectiveness of fiscal policy in macroeconomics. |
| Origin | Developed in the 1970s by economist Arthur Laffer. | Proposed by economist Trygve Haavelmo in 1945. |
| Economic Focus | Taxation and its effect on labor supply, incentives, and total tax revenue. | Fiscal policy's impact on aggregate demand and income through government expenditure. |
| Key Concept | There exists a tax rate between 0% and 100% where tax revenue is maximized; beyond this rate, higher taxes reduce revenue. | Government spending financed by taxation or borrowing leads to an increase in overall demand, measured by a multiplier greater than zero. |
| Policy Implication | Helps policymakers find an optimal tax rate to maximize revenue without harming economic growth. | Justifies active fiscal policy to stimulate the economy, confirming that balanced-budget spending increases national income. |
| Type of Model | Non-linear, dynamic relationship model between tax rate and revenue. | Linear macroeconomic multiplier model for fiscal policy. |
| Mathematical Expression | Tax Revenue = Tax Rate x Tax Base (which depends on the tax rate) | DY = k x DG, where DY is change in national income, DG is change in government spending, and k is the multiplier. |
| Assumptions | Taxpayers respond to tax rate changes by altering work effort or income declaration. | Government spending is fully financed, and prices are fixed in the short run. |
| Relevance | Guides tax policy and debates on taxation limits and economic incentives. | Supports Keynesian fiscal policy and analyses of government expenditure effects. |
Tax Rate Elasticity
Tax rate elasticity measures how sensitive the quantity of taxable income is to changes in the tax rate. Empirical studies indicate that the elasticity of taxable income varies across income groups, typically ranging between 0.1 and 0.4 for average taxpayers, but can be higher for high-income earners. This concept is crucial for policymakers when designing tax systems that balance revenue generation with economic incentives. Understanding tax rate elasticity helps optimize tax rates to minimize efficiency losses and avoid excessive tax avoidance or evasion.
Revenue Maximization
Revenue maximization in economics focuses on increasing a firm's total income by optimizing sales volume and pricing strategies. This concept often involves analyzing the price elasticity of demand to determine the ideal price point that maximizes revenue without significantly reducing quantity sold. Firms use marginal revenue and marginal cost analysis to identify the revenue-maximizing output level, which is where marginal revenue equals zero under certain conditions. Understanding consumer behavior, market structure, and competitive dynamics is essential for effectively implementing revenue maximization strategies.
Fiscal Stimulus Effect
Fiscal stimulus significantly boosts economic activity by increasing government spending or cutting taxes to raise aggregate demand. Empirical studies, such as those from the International Monetary Fund (IMF), show that multipliers for fiscal stimulus in advanced economies can range from 0.8 to 1.5, indicating each dollar spent generates up to $1.50 in economic output. During the 2008 global financial crisis, the U.S. implemented a $787 billion stimulus package that contributed to GDP growth recovery and lower unemployment rates. The effectiveness varies depending on the economic context, including the existing output gap, monetary policy coordination, and the level of public debt.
Government Spending Multiplier
The government spending multiplier measures the change in aggregate output resulting from a change in government expenditures, typically greater than one in Keynesian economics, indicating a positive multiplier effect on GDP. Empirical studies suggest multipliers range from 0.8 to 1.5 depending on economic conditions, such as recession versus expansion periods, and fiscal policy implementation. Fiscal multipliers tend to be larger during economic downturns when monetary policy is constrained, as shown in research by the International Monetary Fund and the Congressional Budget Office. Accurate estimation of the government spending multiplier informs policymakers on effective fiscal stimulus design to maximize economic growth and employment.
Policy Design Implications
Policy design in economics requires rigorous analysis of market behaviors and incentive structures to achieve efficient resource allocation and social welfare maximization. Effective policies incorporate empirical data, economic modeling, and stakeholder feedback to address issues such as externalities, information asymmetry, and public goods provision. Incorporating adaptive mechanisms ensures policies remain effective amid changing economic conditions and emerging challenges. Evidence-based approaches and continuous evaluation enhance the precision and impact of economic policies on growth, equity, and stability.
Source and External Links
Laffer curve - The Laffer Curve represents a theoretical relationship between tax rates and government tax revenue, suggesting that there is a tax rate that maximizes revenue beyond which increasing tax rates actually reduce revenue.
Resist the Allure of Laffer Curve Logic | Cato at Liberty Blog - The Laffer Curve is a conceptual tool for understanding limits on tax rates but can be misleading if overused, as it focuses on maximizing revenue rather than efficient fiscal policy or appropriate government spending levels.
Taxation in the United States and Europe: Theory and Practice - This book covers theoretical and empirical topics in taxation but does not specifically discuss the Haavelmo theorem or directly compare it to the Laffer Curve.
--- Based on the search results, the Laffer Curve is a concept relating tax rates to tax revenue, highlighting an optimal tax rate to maximize revenue. The Haavelmo theorem, however, is not addressed in these results, but it is an economic theorem related to the effect of government spending on income (fiscal multiplier theory), fundamentally different from the Laffer Curve's focus on taxation and revenue.FAQs
What is the Laffer Curve?
The Laffer Curve illustrates the relationship between tax rates and tax revenue, showing that increasing tax rates beyond a certain point reduces total revenue by discouraging economic activity.
What is the Haavelmo Theorem in economics?
The Haavelmo Theorem states that in an econometric model, if the structural errors are uncorrelated with explanatory variables, the Ordinary Least Squares (OLS) estimator provides unbiased and consistent estimates of the true parameters.
How does the Laffer Curve illustrate the relationship between tax rates and revenue?
The Laffer Curve illustrates that tax revenue increases with higher tax rates up to an optimal point, after which further rate increases lead to decreased revenue due to reduced economic activity and tax compliance.
How does the Haavelmo Theorem explain the impact of government spending on income?
The Haavelmo Theorem demonstrates that an increase in government spending raises national income by more than the initial expenditure due to induced increases in consumption within the Keynesian multiplier framework.
What are the key differences between the Laffer Curve and Haavelmo Theorem concepts?
The Laffer Curve illustrates the relationship between tax rates and tax revenue, showing that increasing tax rates beyond a certain point reduces revenue, while the Haavelmo Theorem asserts that government spending financed by money creation has a positive multiplier effect on national income without crowding out private investment.
How do policymakers use the Laffer Curve and Haavelmo Theorem in fiscal decisions?
Policymakers use the Laffer Curve to identify tax rates that maximize revenue without discouraging economic activity, while they apply the Haavelmo Theorem to assess the expansionary impact of government spending financed by debt on national income.
Which economic situations favor the Laffer Curve versus the Haavelmo Theorem?
High marginal tax rates and over-taxation scenarios favor the Laffer Curve, emphasizing tax rate reductions to boost revenue, while government spending multipliers and balanced budget policies favor the Haavelmo Theorem, highlighting fiscal expansions financed by taxes or debt that increase overall demand.
 calledges.com
calledges.com