Samuelson condition defines the optimal provision of public goods by equating the sum of individual marginal rates of substitution to the marginal cost, ensuring efficient resource allocation. Lindahl equilibrium describes a personalized pricing model where individuals pay for public goods according to their marginal benefit, achieving voluntary funding and efficiency. Explore the differences and practical implications of these economic concepts to deepen your understanding of public goods financing.
Main Difference
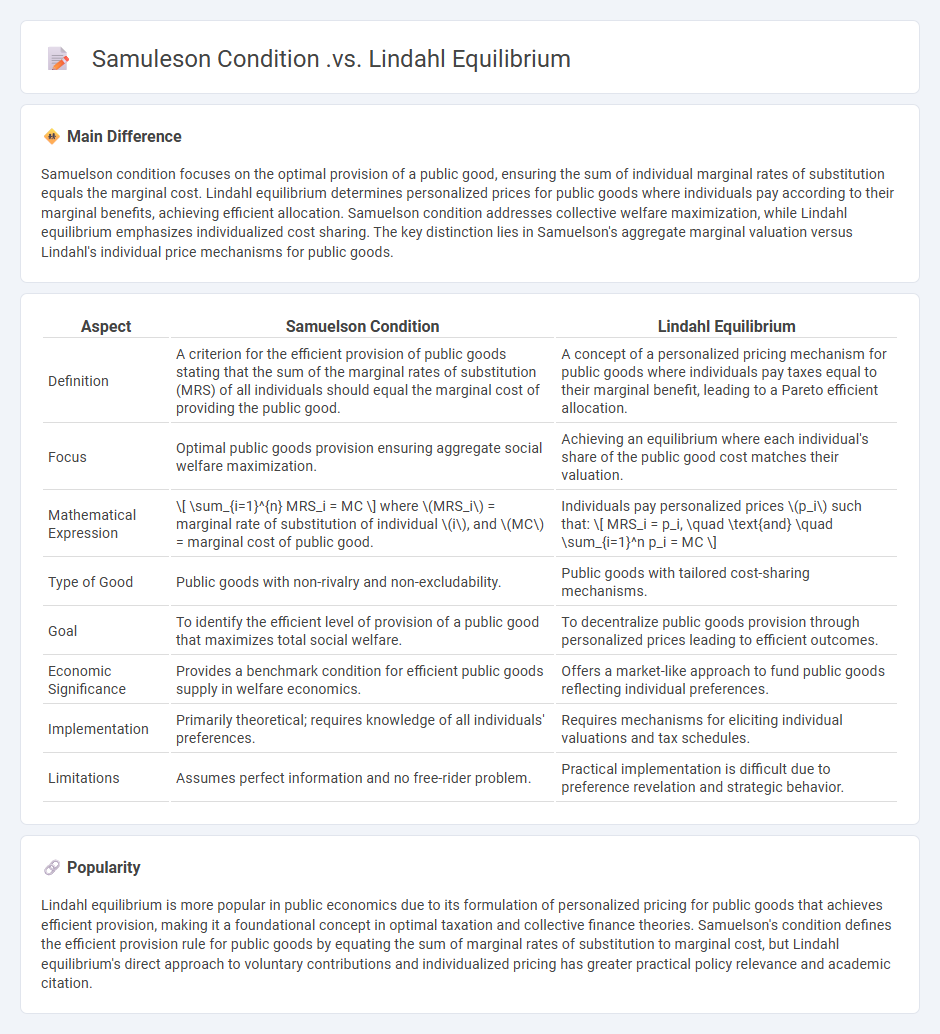
Samuelson condition focuses on the optimal provision of a public good, ensuring the sum of individual marginal rates of substitution equals the marginal cost. Lindahl equilibrium determines personalized prices for public goods where individuals pay according to their marginal benefits, achieving efficient allocation. Samuelson condition addresses collective welfare maximization, while Lindahl equilibrium emphasizes individualized cost sharing. The key distinction lies in Samuelson's aggregate marginal valuation versus Lindahl's individual price mechanisms for public goods.
Connection
Samuelson condition and Lindahl equilibrium both address the efficient provision of public goods by aligning individual preferences with social cost. The Samuelson condition states that the sum of marginal benefits equals the marginal cost, ensuring optimal public good supply. Lindahl equilibrium operationalizes this by assigning personalized prices to individuals so that their weighted demand meets the public good provision at socially efficient levels.
Comparison Table
| Aspect | Samuelson Condition | Lindahl Equilibrium |
|---|---|---|
| Definition | A criterion for the efficient provision of public goods stating that the sum of the marginal rates of substitution (MRS) of all individuals should equal the marginal cost of providing the public good. | A concept of a personalized pricing mechanism for public goods where individuals pay taxes equal to their marginal benefit, leading to a Pareto efficient allocation. |
| Focus | Optimal public goods provision ensuring aggregate social welfare maximization. | Achieving an equilibrium where each individual's share of the public good cost matches their valuation. |
| Mathematical Expression | \[ \sum_{i=1}^{n} MRS_i = MC \] where \(MRS_i\) = marginal rate of substitution of individual \(i\), and \(MC\) = marginal cost of public good. | Individuals pay personalized prices \(p_i\) such that: \[ MRS_i = p_i, \quad \text{and} \quad \sum_{i=1}^n p_i = MC \] |
| Type of Good | Public goods with non-rivalry and non-excludability. | Public goods with tailored cost-sharing mechanisms. |
| Goal | To identify the efficient level of provision of a public good that maximizes total social welfare. | To decentralize public goods provision through personalized prices leading to efficient outcomes. |
| Economic Significance | Provides a benchmark condition for efficient public goods supply in welfare economics. | Offers a market-like approach to fund public goods reflecting individual preferences. |
| Implementation | Primarily theoretical; requires knowledge of all individuals' preferences. | Requires mechanisms for eliciting individual valuations and tax schedules. |
| Limitations | Assumes perfect information and no free-rider problem. | Practical implementation is difficult due to preference revelation and strategic behavior. |
Marginal Rate of Substitution
Marginal Rate of Substitution (MRS) measures the rate at which a consumer is willing to exchange units of one good for another while maintaining the same level of utility. It is calculated as the negative slope of an indifference curve, reflecting the trade-off between two goods. In consumer theory, MRS equals the ratio of the marginal utilities of the goods, expressed as MRS = MUx/MUy. Understanding MRS aids in analyzing consumer choices and market demand behavior.
Marginal Cost of Public Good
Marginal cost of a public good refers to the additional cost incurred to provide one more unit of that good to the public. Unlike private goods, public goods are non-excludable and non-rivalrous, making marginal cost analysis crucial for efficient allocation. In economics, accurately measuring the marginal cost helps governments determine optimal production levels and funding strategies. This concept is pivotal in addressing free-rider problems and ensuring equitable access to public goods such as national defense or public parks.
Personalized Prices
Personalized pricing in economics refers to the strategy where sellers set prices for goods or services based on individual customer data, such as purchase history, demographics, and browsing behavior. This pricing method leverages algorithms and big data analytics to maximize revenue by capturing consumer surplus more effectively. Studies indicate that personalized pricing can increase firms' profits by up to 20%, but it raises ethical concerns related to fairness and privacy. Regulatory frameworks, such as the European Union's General Data Protection Regulation (GDPR), impose restrictions on data use to protect consumer rights in personalized pricing models.
Pareto Efficiency
Pareto efficiency occurs when resources are allocated in a way that no individual can be made better off without making someone else worse off. This concept is fundamental in welfare economics and helps evaluate the optimal distribution of goods and services. Real-world applications include market equilibria analysis and policy design aiming to improve collective well-being. Economic models often use Pareto efficiency to assess trade-offs between equity and efficiency in resource allocation.
Aggregate Willingness to Pay
Aggregate willingness to pay represents the total amount that all consumers in a market are prepared to spend to obtain a good or service, reflecting the combined value individuals assign to it. This measure is crucial in economics for evaluating consumer surplus, policy impacts, and market efficiency. It is derived by summing individual willingness to pay across the entire population or market segment, often illustrated through demand curves. Accurate estimation of aggregate willingness to pay aids in optimal resource allocation and cost-benefit analysis in public economics.
Source and External Links
Samuelson condition - The Samuelson condition states that the efficient provision of public goods requires the sum of individuals' marginal rates of substitution (MRS) between the public good and a private good to equal the marginal rate of transformation (MRT) for the economy, ensuring aggregate marginal benefit equals marginal cost.
Lindahl equilibrium - Lindahl equilibrium is a normative allocation where each individual pays a personalized price (Lindahl price) for the public good, summing to the total cost, and the resulting allocation satisfies the Samuelson condition for efficiency.
Difference between Samuelson and Lindahl - The Samuelson condition identifies the efficient level of public good provision through a mathematical rule, while the Lindahl equilibrium describes a decentralized mechanism--relying on personalized prices--that can achieve this efficient outcome, though it is more prescriptive than a practical market process.
FAQs
What is the Samuelson condition?
The Samuelson condition states that the sum of the marginal rates of substitution between a public good and a private good across all individuals must equal the marginal cost of providing the public good for efficient public good provision.
What is the Lindahl equilibrium?
The Lindahl equilibrium is a concept in public economics where individuals pay personalized prices for public goods reflecting their marginal benefit, resulting in an efficient provision level that equates aggregate willingness to pay with the cost of supply.
How does the Samuelson condition define public good efficiency?
The Samuelson condition defines public good efficiency by stating that the sum of all individuals' marginal rates of substitution between the public good and a private good equals the marginal cost of providing the public good.
How does the Lindahl equilibrium achieve fair cost sharing for public goods?
The Lindahl equilibrium achieves fair cost sharing for public goods by assigning personalized prices to individuals based on their marginal valuation of the public good, ensuring that each pays according to their benefit and the total contributions cover the provision cost.
What are the key differences between Samuelson condition and Lindahl equilibrium?
Samuelson condition determines the optimal provision of public goods by equating the sum of individual marginal rates of substitution to the marginal cost, while Lindahl equilibrium achieves efficient public good provision through personalized prices that balance individual demand with cost, ensuring voluntary participation and budget balance.
Why is the Samuelson condition important for public goods provision?
The Samuelson condition is important for public goods provision because it ensures the efficient allocation by equating the sum of the marginal rates of substitution of all individuals to the marginal cost of providing the public good.
What challenges arise in applying Lindahl equilibrium in real economies?
Lindahl equilibrium faces challenges in real economies due to the difficulty of accurately determining individual preference valuations, the need for complete information, strategic manipulation by agents, complexity in aggregating diverse preferences, and issues with incentive compatibility and free-rider problems.
 calledges.com
calledges.com