Backward induction is a solution concept in game theory used to analyze sequential games by reasoning backward from the end of the game to determine optimal strategies. Subgame perfection refines this concept by requiring that strategies constitute a Nash equilibrium in every subgame, ensuring credible threats and promises. Explore the nuances between backward induction and subgame perfection to deepen your understanding of strategic decision-making.
Main Difference
Backward induction is a method used to solve finite extensive-form games by analyzing the game from the end and reasoning backward to determine optimal strategies at every decision node. Subgame perfection is a refinement of Nash equilibrium that requires strategies to constitute a Nash equilibrium in every subgame of the original game, ensuring consistency and credibility of threats and promises. While backward induction identifies subgame perfect equilibria in games with perfect information, subgame perfection applies to a broader set of games, including those with imperfect information and multiple equilibria. The key distinction lies in backward induction being a solution procedure, whereas subgame perfection defines a solution concept emphasizing equilibrium stability within each subgame.
Connection
Backward induction is a method used to solve finite extensive-form games by analyzing decisions from the end of the game to the beginning. Subgame perfect equilibrium is a refinement of Nash equilibrium where strategies constitute a Nash equilibrium in every subgame, ensuring credibility of threats and promises. The process of backward induction identifies the subgame perfect equilibrium by systematically eliminating non-credible strategies across all subgames.
Comparison Table
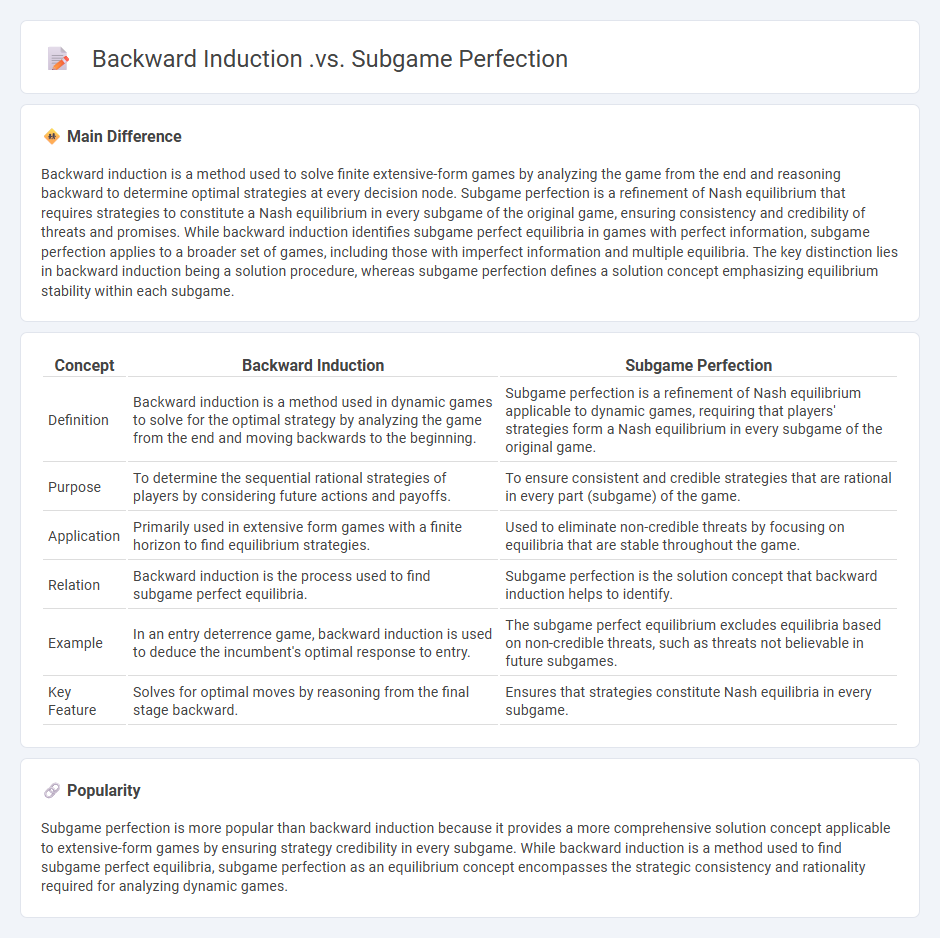
| Concept | Backward Induction | Subgame Perfection |
|---|---|---|
| Definition | Backward induction is a method used in dynamic games to solve for the optimal strategy by analyzing the game from the end and moving backwards to the beginning. | Subgame perfection is a refinement of Nash equilibrium applicable to dynamic games, requiring that players' strategies form a Nash equilibrium in every subgame of the original game. |
| Purpose | To determine the sequential rational strategies of players by considering future actions and payoffs. | To ensure consistent and credible strategies that are rational in every part (subgame) of the game. |
| Application | Primarily used in extensive form games with a finite horizon to find equilibrium strategies. | Used to eliminate non-credible threats by focusing on equilibria that are stable throughout the game. |
| Relation | Backward induction is the process used to find subgame perfect equilibria. | Subgame perfection is the solution concept that backward induction helps to identify. |
| Example | In an entry deterrence game, backward induction is used to deduce the incumbent's optimal response to entry. | The subgame perfect equilibrium excludes equilibria based on non-credible threats, such as threats not believable in future subgames. |
| Key Feature | Solves for optimal moves by reasoning from the final stage backward. | Ensures that strategies constitute Nash equilibria in every subgame. |
Sequential Rationality
Sequential rationality in economics refers to the condition where economic agents make optimal decisions at every stage of a sequential decision-making process, taking into account the history of previous actions and information. This concept is fundamental in dynamic game theory and extensive-form games, ensuring that strategies remain credible and consistent over time. Empirical studies in markets with sequential moves, such as bargaining or investment timing, demonstrate that agents update beliefs and optimize strategies based on observed actions, aligning with sequential rationality principles. The refinement of equilibrium concepts like subgame perfect equilibrium relies heavily on the assumption of sequential rationality to predict stable outcomes in economic models.
Nash Equilibrium
Nash Equilibrium represents a fundamental concept in game theory where no player can benefit by changing their strategy unilaterally, assuming the strategies of others remain constant. This equilibrium occurs when every participant's strategy is optimal given the strategies chosen by all other players. Developed by mathematician John Nash, it applies extensively in economics to analyze competitive markets, auctions, and bargaining scenarios. Practical applications include oligopoly pricing, where firms' strategies stabilize without incentive to deviate.
Subgame Perfect Equilibrium
Subgame Perfect Equilibrium (SPE) is a refinement of Nash Equilibrium applied in dynamic games with sequential moves, ensuring that players' strategies constitute a Nash Equilibrium in every subgame. SPE eliminates non-credible threats by requiring strategies to be optimal at every possible decision point, making it integral in analyzing economic models of bargaining, oligopoly competition, and contract design. For example, in the Stackelberg competition model, the leader firm's commitment shapes the follower's best response, resulting in a SPE that predicts market outcomes accurately. SPE provides critical insights into strategic decision-making where timing and commitment affect economic agents' behavior.
Decision Tree
A decision tree in economics is a diagrammatic tool used to map out possible outcomes, decisions, and their associated risks or rewards, facilitating strategic planning and investment analysis. It incorporates probabilities and payoffs to evaluate different economic decisions, allowing analysts to choose options that maximize expected utility or profit. This method is particularly valuable in cost-benefit analysis, market forecasting, and resource allocation under uncertainty. Prominent applications include capital budgeting decisions and policy impact assessments where future economic scenarios are uncertain.
Credible Threats
Credible threats in economics play a crucial role in strategic interactions and game theory, influencing decision-making and negotiation outcomes. These threats must be believable and enforceable to effectively alter the behavior of other economic agents, such as firms or governments. For example, a credible threat of a price war can deter competitors from entering a market or engaging in aggressive pricing strategies. The effectiveness of credible threats depends on the rationality of the actors and the transparency of their intentions in economic environments.
Source and External Links
Chapter 11 Subgame-Perfect Nash Equilibrium - Backward induction is a solution method for finite, perfect information games, while subgame perfect equilibrium is a broader concept requiring that the strategy profile be a Nash equilibrium in every subgame of the game.
Subgame perfect equilibrium (Wikipedia) - Backward induction is commonly used to find subgame perfect equilibria in finite games, but subgame perfection is defined for all dynamic games, not just those solvable by backward induction.
Backward induction and subgame perfection - All solutions found by backward induction are Nash equilibria and are special cases of subgame perfect equilibria, but not all Nash equilibria are subgame perfect.
FAQs
What is backward induction in game theory?
Backward induction in game theory is a method used to solve finite sequential games by analyzing the game from the end and reasoning backward to determine optimal strategies at each decision point.
How does subgame perfection differ from backward induction?
Subgame perfection is a solution concept requiring strategies to constitute a Nash equilibrium in every subgame, while backward induction is a method used to find subgame perfect equilibria by solving from the end of the game tree backward.
When do you use backward induction?
Use backward induction to solve finite extensive-form games by analyzing decisions from the end of the game to the beginning.
What is a subgame in extensive form games?
A subgame in extensive form games is a part of the game that starts at a single decision node, includes all its successors, and forms a game itself satisfying the perfect recall condition.
Can every subgame perfect equilibrium be found using backward induction?
Every subgame perfect equilibrium in a finite extensive-form game with perfect information can be found using backward induction.
Why is subgame perfect equilibrium important?
Subgame perfect equilibrium is important because it ensures strategy credibility by eliminating non-credible threats, guaranteeing consistent optimal decisions in every subgame of a dynamic game.
How does backward induction help identify optimal strategies?
Backward induction identifies optimal strategies by analyzing a game from its end states to the beginning, systematically determining the best action at each decision point based on subsequent outcomes.
 calledges.com
calledges.com