Mesh Analysis and Nodal Analysis are fundamental techniques in electrical circuit theory used to determine current and voltage distributions. Mesh Analysis focuses on loop currents in planar circuits, simplifying complex networks by applying Kirchhoff's Voltage Law, while Nodal Analysis uses node voltages with Kirchhoff's Current Law to analyze circuits systematically. Explore the detailed differences and applications of these methods to enhance your circuit analysis skills.
Main Difference
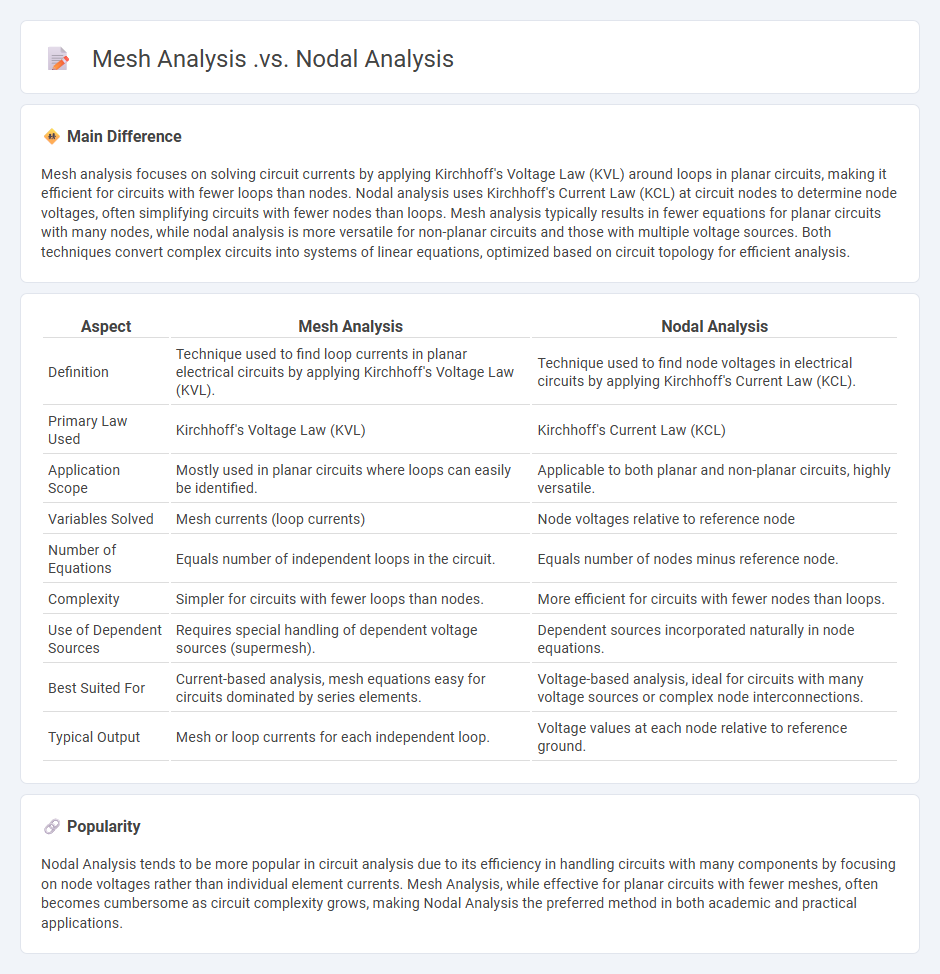
Mesh analysis focuses on solving circuit currents by applying Kirchhoff's Voltage Law (KVL) around loops in planar circuits, making it efficient for circuits with fewer loops than nodes. Nodal analysis uses Kirchhoff's Current Law (KCL) at circuit nodes to determine node voltages, often simplifying circuits with fewer nodes than loops. Mesh analysis typically results in fewer equations for planar circuits with many nodes, while nodal analysis is more versatile for non-planar circuits and those with multiple voltage sources. Both techniques convert complex circuits into systems of linear equations, optimized based on circuit topology for efficient analysis.
Connection
Mesh Analysis and Nodal Analysis are interconnected circuit analysis methods that simplify solving electrical networks by focusing on different variables; Mesh Analysis analyzes loop currents in planar circuits, while Nodal Analysis examines node voltages. Both techniques apply Kirchhoff's laws--Mesh Analysis uses Kirchhoff's Voltage Law (KVL) and Nodal Analysis utilizes Kirchhoff's Current Law (KCL)--to establish systems of equations representing the circuit's behavior. These methods are complementary and can be converted into each other's frameworks, enabling engineers to choose the most efficient approach for analyzing complex electrical circuits.
Comparison Table
| Aspect | Mesh Analysis | Nodal Analysis |
|---|---|---|
| Definition | Technique used to find loop currents in planar electrical circuits by applying Kirchhoff's Voltage Law (KVL). | Technique used to find node voltages in electrical circuits by applying Kirchhoff's Current Law (KCL). |
| Primary Law Used | Kirchhoff's Voltage Law (KVL) | Kirchhoff's Current Law (KCL) |
| Application Scope | Mostly used in planar circuits where loops can easily be identified. | Applicable to both planar and non-planar circuits, highly versatile. |
| Variables Solved | Mesh currents (loop currents) | Node voltages relative to reference node |
| Number of Equations | Equals number of independent loops in the circuit. | Equals number of nodes minus reference node. |
| Complexity | Simpler for circuits with fewer loops than nodes. | More efficient for circuits with fewer nodes than loops. |
| Use of Dependent Sources | Requires special handling of dependent voltage sources (supermesh). | Dependent sources incorporated naturally in node equations. |
| Best Suited For | Current-based analysis, mesh equations easy for circuits dominated by series elements. | Voltage-based analysis, ideal for circuits with many voltage sources or complex node interconnections. |
| Typical Output | Mesh or loop currents for each independent loop. | Voltage values at each node relative to reference ground. |
Loop Currents
Loop currents in engineering refer to unintended circulating currents that occur in closed conductive loops within electrical systems, often causing interference or energy losses. These currents can arise from electromagnetic induction, particularly in power distribution networks, PCB designs, and grounding systems. Proper layout techniques, such as minimizing loop area and employing twisted pair wiring, help reduce loop current effects. Accurate analysis and mitigation are critical in enhancing system reliability and electromagnetic compatibility (EMC).
Node Voltages
Node voltages represent the electrical potentials at specific points within an electrical circuit, measured relative to a common reference node, often ground. They are fundamental in circuit analysis techniques such as the Node Voltage Method, which simplifies complex circuits by applying Kirchhoff's Current Law (KCL) at each node. Accurate calculation of node voltages enables the determination of current flows and power distribution in resistive, capacitive, and inductive networks. This approach is widely utilized in engineering disciplines for designing and analyzing electrical systems, including integrated circuits and power distribution networks.
Kirchhoff's Voltage Law (KVL)
Kirchhoff's Voltage Law (KVL) states that the algebraic sum of all voltages around any closed electrical circuit loop is zero, ensuring energy conservation in electrical engineering. This fundamental principle applies to both direct current (DC) and alternating current (AC) circuits, enabling accurate analysis and design of complex electrical networks. Engineers utilize KVL to determine unknown voltages, optimize circuit performance, and verify electrical system functionality in applications ranging from power distribution to electronic devices. The law complements Kirchhoff's Current Law (KCL) to provide a complete framework for circuit analysis.
Kirchhoff's Current Law (KCL)
Kirchhoff's Current Law (KCL) states that the total current entering a junction or node in an electrical circuit equals the total current leaving the node, ensuring conservation of electric charge. This principle is fundamental in circuit analysis for designing and troubleshooting electrical systems across various engineering fields. KCL applies to both direct current (DC) and alternating current (AC) circuits, providing a basis for nodal analysis and complex circuit simulations. Engineers rely on KCL to ensure accurate current distribution and system stability in electronic and power engineering applications.
Planar Circuits
Planar circuits are integral to modern electronics, offering compact, reliable, and cost-effective solutions for signal processing in engineering applications. These circuits are fabricated on flat substrates, typically silicon or ceramic, enabling high-density integration of components such as resistors, capacitors, and transistors. The planar technology supports the creation of complex microelectronic devices, including integrated circuits (ICs) used in telecommunications, automotive systems, and consumer electronics. Advancements in photolithography and semiconductor fabrication have continually enhanced the performance and scalability of planar circuits.
Source and External Links
Mesh and Node Analysis - Student Circuit - This webpage compares mesh and nodal analysis methods, explaining that nodal analysis uses Kirchhoff's current law for node voltages, while mesh analysis uses Kirchhoff's voltage law for mesh currents.
Mesh Analysis - BYJU'S - This resource describes mesh analysis as an application of Kirchhoff's voltage law to calculate currents in planar circuits, contrasting it with nodal analysis.
How to Decide Node vs Mesh - This video discusses considerations for choosing between node voltage and mesh current analysis, highlighting the number of nodes and meshes as key factors.
FAQs
What is Mesh Analysis in electrical circuits?
Mesh Analysis is a systematic method in electrical circuits for determining the currents flowing in each mesh by applying Kirchhoff's Voltage Law (KVL) around loops.
What is Nodal Analysis in electrical circuits?
Nodal Analysis is a method in electrical circuits used to determine the voltage at each node by applying Kirchhoff's Current Law (KCL) and solving the resulting system of equations.
What is the main difference between Mesh Analysis and Nodal Analysis?
Mesh Analysis focuses on solving circuit currents by applying Kirchhoff's Voltage Law (KVL) around loops, while Nodal Analysis solves for node voltages using Kirchhoff's Current Law (KCL) at circuit junctions.
When should you use Mesh Analysis instead of Nodal Analysis?
Use Mesh Analysis when the circuit has fewer loops than nodes, contains mostly planar circuits, and voltage sources are easier to handle in loops.
What are the advantages of Mesh Analysis?
Mesh Analysis simplifies solving complex electrical circuits by reducing the number of equations through loop currents, facilitates systematic application of Kirchhoff's Voltage Law, efficiently handles planar circuits, and directly provides branch currents for design and analysis.
What are the benefits of Nodal Analysis?
Nodal Analysis simplifies circuit equations by reducing the number of variables, provides a systematic approach for analyzing complex electrical circuits, improves accuracy in calculating node voltages, and facilitates the use of matrix methods for solving large networks efficiently.
Can Mesh and Nodal Analysis be used together in a circuit?
Mesh and Nodal Analysis can be combined in a circuit by applying Mesh Analysis to planar sections and Nodal Analysis to non-planar or complex nodes, optimizing solution efficiency.
 calledges.com
calledges.com