Multibody dynamics analyzes systems of interconnected bodies undergoing complex motions with forces and constraints, capturing flexibility and interactions between components. Rigid body dynamics simplifies these systems by assuming bodies are perfectly stiff, focusing on linear and rotational motion without deformation. Discover the key differences and applications of both approaches to enhance your mechanical system simulations and designs.
Main Difference
Multibody Dynamics focuses on analyzing the motion and interaction of interconnected bodies with joints, allowing for relative movement and deformation, whereas Rigid Body Dynamics assumes bodies do not deform and studies the motion of solid objects as a whole unit. Multibody Dynamics models complex systems like robotic arms or vehicle suspensions with multiple degrees of freedom, while Rigid Body Dynamics applies primarily to simpler systems with fewer components. Computationally, Multibody Dynamics involves solving nonlinear equations for joint constraints and flexible connections, whereas Rigid Body Dynamics often uses simpler, linear equations for objects moving under forces and torques. Understanding these distinctions is crucial for accurate simulation in mechanical engineering and robotics applications.
Connection
Multibody dynamics and rigid body dynamics are interconnected as multibody dynamics extends rigid body principles to systems composed of multiple interconnected bodies. Rigid body dynamics focuses on the motion and forces of individual solid bodies assuming no deformation, while multibody dynamics analyzes the complex interactions and relative movements within assemblies of these rigid bodies through joints and constraints. This connection enables accurate modeling and simulation of mechanical systems such as robotic arms, vehicle suspensions, and biomechanical structures.
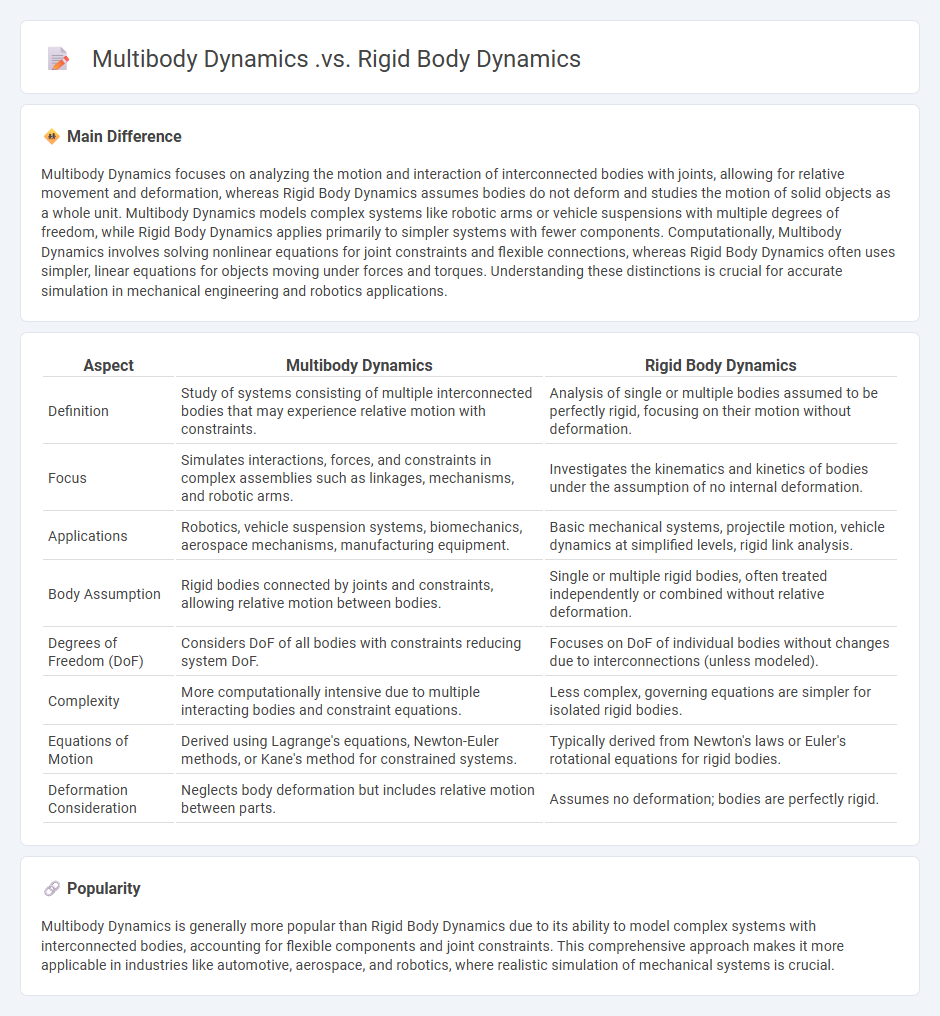
Comparison Table
| Aspect | Multibody Dynamics | Rigid Body Dynamics |
|---|---|---|
| Definition | Study of systems consisting of multiple interconnected bodies that may experience relative motion with constraints. | Analysis of single or multiple bodies assumed to be perfectly rigid, focusing on their motion without deformation. |
| Focus | Simulates interactions, forces, and constraints in complex assemblies such as linkages, mechanisms, and robotic arms. | Investigates the kinematics and kinetics of bodies under the assumption of no internal deformation. |
| Applications | Robotics, vehicle suspension systems, biomechanics, aerospace mechanisms, manufacturing equipment. | Basic mechanical systems, projectile motion, vehicle dynamics at simplified levels, rigid link analysis. |
| Body Assumption | Rigid bodies connected by joints and constraints, allowing relative motion between bodies. | Single or multiple rigid bodies, often treated independently or combined without relative deformation. |
| Degrees of Freedom (DoF) | Considers DoF of all bodies with constraints reducing system DoF. | Focuses on DoF of individual bodies without changes due to interconnections (unless modeled). |
| Complexity | More computationally intensive due to multiple interacting bodies and constraint equations. | Less complex, governing equations are simpler for isolated rigid bodies. |
| Equations of Motion | Derived using Lagrange's equations, Newton-Euler methods, or Kane's method for constrained systems. | Typically derived from Newton's laws or Euler's rotational equations for rigid bodies. |
| Deformation Consideration | Neglects body deformation but includes relative motion between parts. | Assumes no deformation; bodies are perfectly rigid. |
Degrees of Freedom (DOF)
Degrees of Freedom (DOF) in engineering refer to the number of independent parameters that define the motion or configuration of a mechanical system. For a rigid body in three-dimensional space, there are typically six DOF: three translational movements along the x, y, and z axes, and three rotational movements about these axes. Understanding DOF is crucial for the design and analysis of mechanisms, robotics, and control systems, as it determines the system's ability to maneuver and perform tasks. Engineers use DOF calculations to optimize system flexibility, stability, and functionality in applications ranging from robotic arms to vehicle suspensions.
Flexible Bodies
Flexible bodies in engineering refer to structures or components designed to deform under load without permanent damage, enhancing performance in applications such as robotics, aerospace, and civil engineering. Analysis techniques include finite element methods (FEM) and multi-body dynamics to predict stress, strain, and vibration responses. Materials like shape memory alloys and advanced composites improve flexibility while maintaining strength and durability. Controlling flexible body dynamics optimizes system stability and longevity in complex mechanical systems.
Constraint Equations
Constraint equations in engineering define relationships between variables to restrict system behavior and ensure compatibility with design requirements. These equations are essential in fields like mechanical, civil, and aerospace engineering for modeling structures, mechanisms, and control systems accurately. By expressing physical limits such as geometric configurations, motion restrictions, and material properties, constraint equations facilitate simulation, analysis, and optimization processes. Advanced applications include finite element analysis, robotics kinematics, and multibody system dynamics, where solving constraint equations ensures system stability and performance.
Kinematic Chains
Kinematic chains consist of interconnected rigid bodies called links connected by joints that constrain their relative motion, forming a mechanical system for transmitting motion and force. These chains are fundamental in robotic arms, machinery, and automotive suspensions, enabling precise control and movement. The analysis of kinematic chains involves studying degrees of freedom, mobility, and the synthesis of motion paths to optimize mechanical performance. Understanding these chains enhances the design of efficient, reliable engineering systems with improved dynamic response and stability.
Nonlinear Motion
Nonlinear motion in engineering refers to systems where displacement is not directly proportional to applied forces, resulting in complex behavior such as chaos, bifurcations, and resonance. Common examples include the nonlinear vibrations of mechanical structures, fluid dynamics in turbulent flow, and robotic manipulators with flexible joints. Engineers use tools like perturbation methods, numerical simulations, and phase space analysis to predict and control these motions. Understanding nonlinear motion is critical in designing stable, efficient systems in aerospace, automotive, and civil engineering applications.
Source and External Links
Multibody system - Wikipedia - Multibody dynamics studies the behavior of interconnected rigid or flexible bodies with large translational and rotational displacements, while rigid body dynamics typically focuses on the motion of individual rigid bodies without considering complex interconnections or constraints between multiple bodies.
What is Multibody Dynamics Simulation? - Ansys - Multibody dynamics simulation models and predicts the behavior of systems with many interconnected bodies in motion, essential for understanding the overall system behavior, whereas rigid body dynamics involves analysis primarily of separate, individual rigid bodies.
What is the difference between Rigid Dynamics and Transient Dynamics? - Rigid body dynamics handles large motions and rotations for a relatively small number of degrees of freedom with nonlinear equations and adaptive time stepping, focusing on pure rigid bodies, whereas multibody dynamics deals with multiple interconnected bodies and their constraints in motion.
FAQs
What is Multibody Dynamics?
Multibody dynamics is the study of the motion and interaction of interconnected rigid or flexible bodies under forces and constraints in mechanical systems.
What is Rigid Body Dynamics?
Rigid Body Dynamics studies the motion and forces of solid objects assuming they do not deform under applied forces.
How do Multibody Dynamics and Rigid Body Dynamics differ?
Multibody Dynamics studies interconnected bodies with relative motion and joint constraints, while Rigid Body Dynamics analyzes motion of a single or multiple bodies assuming no deformation.
What are the main applications of Multibody Dynamics?
Multibody Dynamics is primarily applied in automotive engineering for vehicle dynamics simulation, robotics for motion analysis and control, aerospace for spacecraft and aircraft mechanism design, biomechanics for human movement study, and machinery design for analyzing mechanical system behavior.
What are the assumptions behind Rigid Body Dynamics?
Rigid Body Dynamics assumes that bodies are perfectly rigid with no deformation, mass distribution remains constant, motion occurs in a fixed reference frame, and external forces and torques act on the body without altering its shape.
How does flexibility affect Multibody Dynamics systems?
Flexibility in Multibody Dynamics systems enhances realistic modeling by accounting for elastic deformations, which affects vibration analysis, stability, and precision in motion prediction.
Why is Multibody Dynamics important in engineering analysis?
Multibody Dynamics is crucial in engineering analysis because it accurately models and simulates the motion and interaction of interconnected rigid or flexible bodies, enabling prediction of mechanical behavior, optimization of system performance, and prevention of failures in complex machinery and structures.
 calledges.com
calledges.com