Rectilinear flow occurs when fluid particles move along straight, parallel paths, typically observed in laminar flow conditions with minimal disturbance. Rotational flow involves fluid elements rotating around their own axes, characterized by non-zero vorticity and the presence of vortices or swirling motion in the fluid. Explore the detailed differences and applications of rectilinear and rotational flow for a deeper understanding of fluid dynamics.
Main Difference
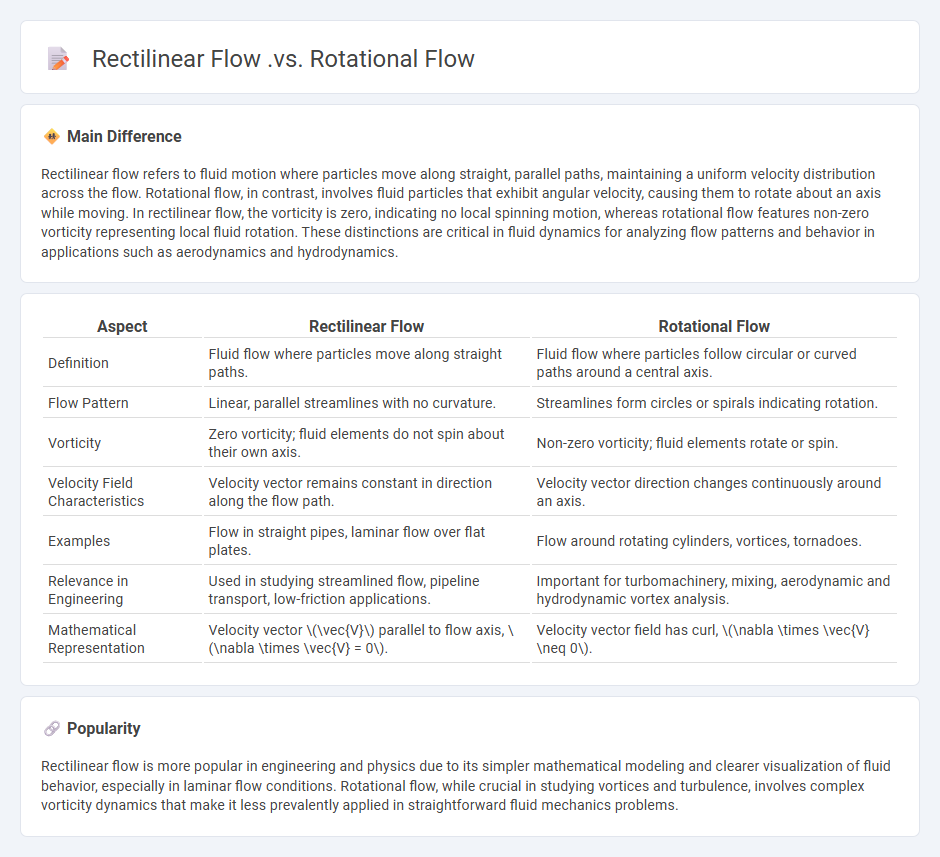
Rectilinear flow refers to fluid motion where particles move along straight, parallel paths, maintaining a uniform velocity distribution across the flow. Rotational flow, in contrast, involves fluid particles that exhibit angular velocity, causing them to rotate about an axis while moving. In rectilinear flow, the vorticity is zero, indicating no local spinning motion, whereas rotational flow features non-zero vorticity representing local fluid rotation. These distinctions are critical in fluid dynamics for analyzing flow patterns and behavior in applications such as aerodynamics and hydrodynamics.
Connection
Rectilinear flow and rotational flow are connected through the velocity field characteristics in fluid dynamics, where rectilinear flow implies motion along straight paths with zero vorticity, whereas rotational flow involves circular or swirling motion with non-zero vorticity. The transition between these flows can be analyzed by examining the curl of the velocity vector field, which quantifies the local rotation of fluid elements. Understanding this relationship aids in modeling complex fluid behavior, especially in turbulence and vortex formation studies.
Comparison Table
| Aspect | Rectilinear Flow | Rotational Flow |
|---|---|---|
| Definition | Fluid flow where particles move along straight paths. | Fluid flow where particles follow circular or curved paths around a central axis. |
| Flow Pattern | Linear, parallel streamlines with no curvature. | Streamlines form circles or spirals indicating rotation. |
| Vorticity | Zero vorticity; fluid elements do not spin about their own axis. | Non-zero vorticity; fluid elements rotate or spin. |
| Velocity Field Characteristics | Velocity vector remains constant in direction along the flow path. | Velocity vector direction changes continuously around an axis. |
| Examples | Flow in straight pipes, laminar flow over flat plates. | Flow around rotating cylinders, vortices, tornadoes. |
| Relevance in Engineering | Used in studying streamlined flow, pipeline transport, low-friction applications. | Important for turbomachinery, mixing, aerodynamic and hydrodynamic vortex analysis. |
| Mathematical Representation | Velocity vector \(\vec{V}\) parallel to flow axis, \(\nabla \times \vec{V} = 0\). | Velocity vector field has curl, \(\nabla \times \vec{V} \neq 0\). |
Streamline pattern
A streamline pattern in engineering represents the trajectory followed by fluid particles as they flow smoothly around obstacles, indicating direction and velocity without turbulence. These patterns help engineers analyze aerodynamic designs by visualizing how air or liquid moves past surfaces, minimizing drag and optimizing performance. Computational fluid dynamics (CFD) tools generate precise streamline patterns to improve efficiency in aerospace, automotive, and civil engineering projects. Understanding these flow lines supports the design of pumps, turbines, and ventilation systems by ensuring smooth fluid motion.
Velocity distribution
Velocity distribution in engineering describes how fluid velocity varies across a cross-section of a flow field, crucial for understanding fluid dynamics in pipes, ducts, and open channels. In laminar flow, the velocity profile is parabolic, with maximum velocity at the center and zero at the boundary due to the no-slip condition. Turbulent flow exhibits a flatter velocity profile with a thin boundary layer near solid surfaces, influenced by factors such as Reynolds number and surface roughness. Analyzing velocity distribution helps optimize fluid transport systems, enhance heat transfer, and predict pressure drops in engineering applications.
Vorticity
Vorticity in engineering quantifies the local rotation of fluid elements, critical for analyzing turbulent flows and aerodynamic performance. It is mathematically defined as the curl of the velocity field, representing the microscopic spin within a fluid. Understanding vorticity aids in optimizing designs of aircraft wings, turbines, and combustion systems by predicting vortex behavior and flow separation. Computational Fluid Dynamics (CFD) simulations frequently employ vorticity to visualize and control complex flow patterns for enhanced efficiency and stability.
Irrotational flow
Irrotational flow describes a fluid motion where the vorticity is zero, meaning the flow has no local spinning or rotation at any point. This concept is essential in potential flow theory, where the velocity field can be expressed as the gradient of a scalar potential function, ensuring divergence-free and curl-free behavior. Engineers apply irrotational flow principles in aerodynamics to simplify the analysis of incompressible, inviscid flows around airfoils and streamline designs. Computational fluid dynamics (CFD) models often assume irrotational flow to reduce complexity while accurately predicting lift and pressure distribution.
Fluid machinery applications
Fluid machinery plays a crucial role in engineering by enabling the efficient conversion of fluid energy into mechanical energy and vice versa. Common applications include pumps, turbines, compressors, and fans, which are essential in industries like power generation, water treatment, HVAC systems, and chemical processing. Turbomachinery, such as steam turbines and hydraulic turbines, contributes significantly to electricity production worldwide. Advances in computational fluid dynamics enhance the design and optimization of these machines, improving performance and energy efficiency.
Source and External Links
Fluid Mechanics Unit 3- Flow Kinematics - Defines rotational flow as fluid particles rotating about their mass centers while moving, and irrotational flow as having no such rotation, focusing on the fluid particle motion and rotation components in flow kinematics.
Potential flow - Wikipedia - Describes irrotational flow (potential flow) as fluid flow with zero vorticity, where velocity can be expressed as the gradient of a velocity potential, in contrast to rotational flow which involves vorticity.
Irrotational/Rotational Flows and Velocity Potentials - Physics Forums - Discusses subtleties in rotational vs. irrotational flow, clarifying that zero curl velocity implies irrotational flow, but global circulation effects may prevent representing velocity simply as a gradient of a potential.
FAQs
What is rectilinear flow?
Rectilinear flow is the fluid motion in which fluid particles move along straight, parallel paths without any rotation or turbulence.
What is rotational flow?
Rotational flow is a fluid motion where the fluid particles exhibit nonzero vorticity, causing them to rotate about their own axes.
How do rectilinear flow and rotational flow differ?
Rectilinear flow features fluid particles moving along straight, parallel paths with zero vorticity, while rotational flow involves fluid particles rotating about their own axes, exhibiting nonzero vorticity.
What are examples of rectilinear flow?
Examples of rectilinear flow include laminar flow in a straight pipe, steady airflow over a flat plate, and uniform flow in open channels.
What causes rotational flow in fluids?
Rotational flow in fluids is caused by the presence of vorticity, which arises from velocity gradients, shear forces, and external torques acting within the fluid.
What are the effects of rotational flow on particles?
Rotational flow causes particles to experience angular velocity, inducing rotation and increased shear stress that affects particle alignment, dispersion, and mixing efficiency.
Why is understanding both flows important in fluid dynamics?
Understanding both laminar and turbulent flows is crucial in fluid dynamics for accurate prediction of fluid behavior, optimizing engineering designs, and improving efficiency in systems such as pipelines, aircraft, and hydraulic machinery.
 calledges.com
calledges.com