Discrete-time signals represent data points at specific intervals, often used in digital systems and signal processing, while continuous-time signals describe values over a continuous range, essential in analog systems such as audio and communication signals. Understanding the differences in sampling, representation, and processing between these signal types is crucial for applications in telecommunications, control systems, and digital audio. Explore further to grasp the practical implications and technical nuances of discrete-time versus continuous-time signals.
Main Difference
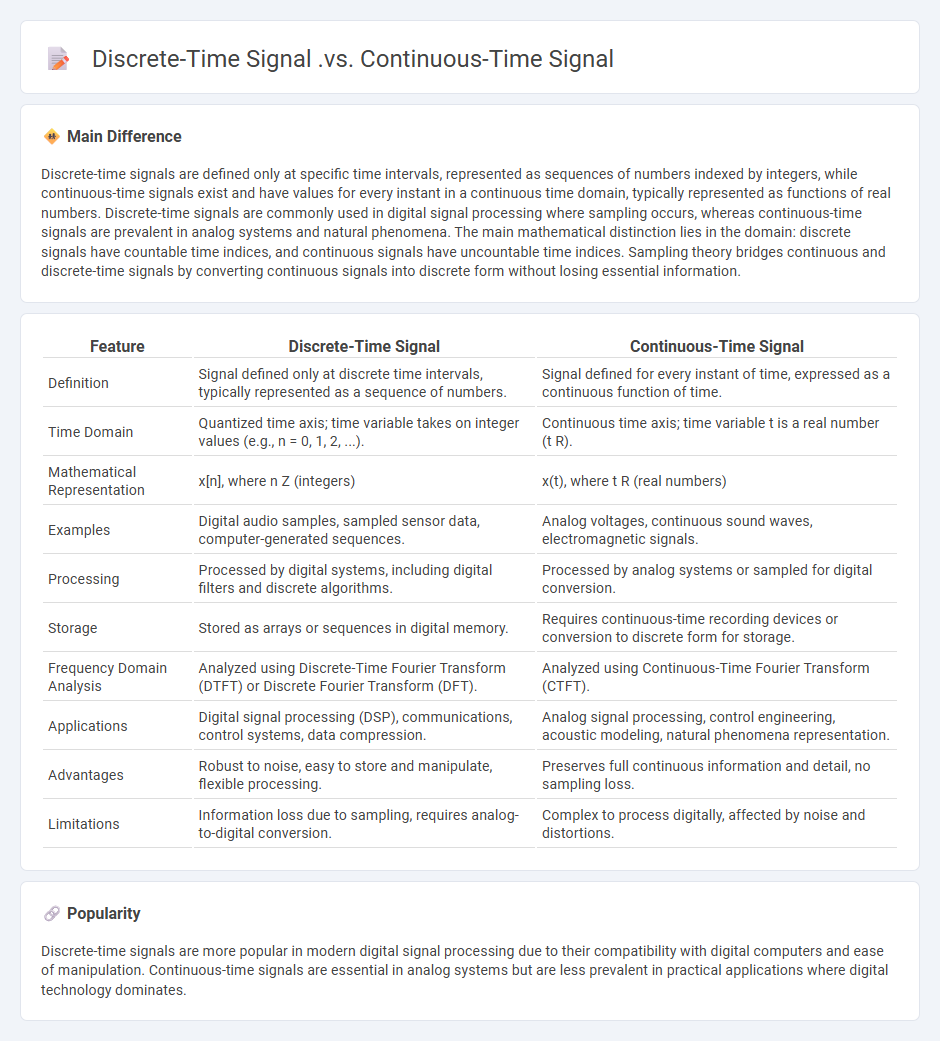
Discrete-time signals are defined only at specific time intervals, represented as sequences of numbers indexed by integers, while continuous-time signals exist and have values for every instant in a continuous time domain, typically represented as functions of real numbers. Discrete-time signals are commonly used in digital signal processing where sampling occurs, whereas continuous-time signals are prevalent in analog systems and natural phenomena. The main mathematical distinction lies in the domain: discrete signals have countable time indices, and continuous signals have uncountable time indices. Sampling theory bridges continuous and discrete-time signals by converting continuous signals into discrete form without losing essential information.
Connection
Discrete-time signals represent sampled versions of continuous-time signals, capturing their values at specific intervals defined by the sampling frequency. The connection between them is established through the sampling theorem, which states that a continuous-time signal can be perfectly reconstructed from its discrete samples if the sampling rate exceeds twice the highest frequency component (Nyquist rate). Digital signal processing relies on this relationship to analyze, modify, and reconstruct continuous signals using discrete data points.
Comparison Table
| Feature | Discrete-Time Signal | Continuous-Time Signal |
|---|---|---|
| Definition | Signal defined only at discrete time intervals, typically represented as a sequence of numbers. | Signal defined for every instant of time, expressed as a continuous function of time. |
| Time Domain | Quantized time axis; time variable takes on integer values (e.g., n = 0, 1, 2, ...). | Continuous time axis; time variable t is a real number (t R). |
| Mathematical Representation | x[n], where n Z (integers) | x(t), where t R (real numbers) |
| Examples | Digital audio samples, sampled sensor data, computer-generated sequences. | Analog voltages, continuous sound waves, electromagnetic signals. |
| Processing | Processed by digital systems, including digital filters and discrete algorithms. | Processed by analog systems or sampled for digital conversion. |
| Storage | Stored as arrays or sequences in digital memory. | Requires continuous-time recording devices or conversion to discrete form for storage. |
| Frequency Domain Analysis | Analyzed using Discrete-Time Fourier Transform (DTFT) or Discrete Fourier Transform (DFT). | Analyzed using Continuous-Time Fourier Transform (CTFT). |
| Applications | Digital signal processing (DSP), communications, control systems, data compression. | Analog signal processing, control engineering, acoustic modeling, natural phenomena representation. |
| Advantages | Robust to noise, easy to store and manipulate, flexible processing. | Preserves full continuous information and detail, no sampling loss. |
| Limitations | Information loss due to sampling, requires analog-to-digital conversion. | Complex to process digitally, affected by noise and distortions. |
Sampling
Sampling in engineering involves selecting representative data points from a larger dataset to analyze system performance, quality control, and material properties. Techniques such as random, stratified, and systematic sampling help engineers ensure accurate measurements while reducing costs and time. In manufacturing, sampling supports defect detection and process optimization, enhancing product reliability. Statistical tools like control charts and hypothesis testing complement sampling to improve decision-making and maintain engineering standards.
Quantization
Quantization in engineering refers to the process of mapping a large set of input values to a smaller set, commonly used in digital signal processing and analog-to-digital conversion. It reduces continuous signals into discrete levels, enabling efficient storage, transmission, and processing in digital systems. This technique is fundamental in applications like audio encoding, image compression, and communications, where bit rate constraints and noise tolerance are critical. Quantization error or noise is a key factor influencing the accuracy and quality of reconstructed signals.
Time Domain
Time domain analysis in engineering focuses on examining signals, systems, and processes with respect to time. It involves studying transient and steady-state responses, enabling engineers to model dynamic behaviors of electrical circuits, mechanical systems, and control systems. Techniques such as time-domain reflectometry (TDR) and impulse response analysis provide detailed insights into system performance and stability. This approach complements frequency domain analysis by directly observing how system variables evolve over time.
Analog Signal
Analog signal refers to a continuous signal that represents physical measurements and varies smoothly over time. It is characterized by infinite resolution and varying amplitude, commonly used in audio, temperature sensing, and radio frequency transmission. Analog engineering involves designing circuits like amplifiers, filters, and modulators to process these signals. Key parameters include frequency, amplitude, phase, and noise level, influencing signal fidelity and performance.
Digital Signal
Digital signals represent discrete-time signals generated by digital modulation, encoding information in binary form for processing, storage, and transmission. They are fundamental in modern communication systems, such as cellular networks and digital audio, enabling robust noise resistance and efficient error correction. Engineering disciplines utilize digital signal processing (DSP) algorithms to filter, compress, and analyze these signals, improving system performance and accuracy. Key technologies include analog-to-digital converters (ADCs), digital-to-analog converters (DACs), and microprocessors specialized for real-time digital signal computation.
Source and External Links
Discrete time and continuous time - Wikipedia - Discrete-time signals are sequences of values defined at specific, separated points in time, while continuous-time signals are functions defined for every instant in an interval.
Continuous Time and Discrete Time Control Systems - GeeksforGeeks - Continuous-time signals change smoothly over time and are represented by continuous functions, whereas discrete-time signals are represented as sequences of values at sampled intervals.
Lecture 1 ELE 301: Signals and Systems - Princeton University - A continuous-time signal has a value at every point in time within its domain, while a discrete-time signal only has values at specific, separate times.
FAQs
What is a discrete-time signal?
A discrete-time signal is a sequence of values or samples defined only at discrete time intervals, often represented as x[n] where n is an integer.
What is a continuous-time signal?
A continuous-time signal is a function defined for every instant of time, representing a physical quantity varying continuously over time.
How do discrete-time and continuous-time signals differ?
Discrete-time signals are defined only at specific time intervals and represented as sequences, while continuous-time signals are defined for every instant in time and represented as continuous functions.
What are examples of discrete-time and continuous-time signals?
Examples of discrete-time signals include digital audio samples, stock price sequences, and monthly sales data. Examples of continuous-time signals include analog audio signals, temperature variations over time, and sinusoidal waveforms like voltage signals in AC circuits.
What are common uses for discrete-time signals?
Discrete-time signals are commonly used in digital signal processing, telecommunications, audio and speech processing, control systems, and digital image processing.
Why is sampling important for signal processing?
Sampling is important for signal processing because it converts continuous-time signals into discrete-time signals, enabling digital representation, storage, and analysis while preserving essential information for accurate reconstruction and processing.
Can continuous-time signals be converted to discrete-time signals?
Continuous-time signals can be converted to discrete-time signals through the process of sampling, which involves measuring signal values at uniform time intervals.
 calledges.com
calledges.com