Statically determinate structures can be analyzed solely using equilibrium equations, making their internal forces and reactions directly solvable. Statically indeterminate structures require additional compatibility conditions and material properties for analysis due to redundant supports or members. Explore detailed comparisons and methods to determine the structural type for accurate engineering design.
Main Difference
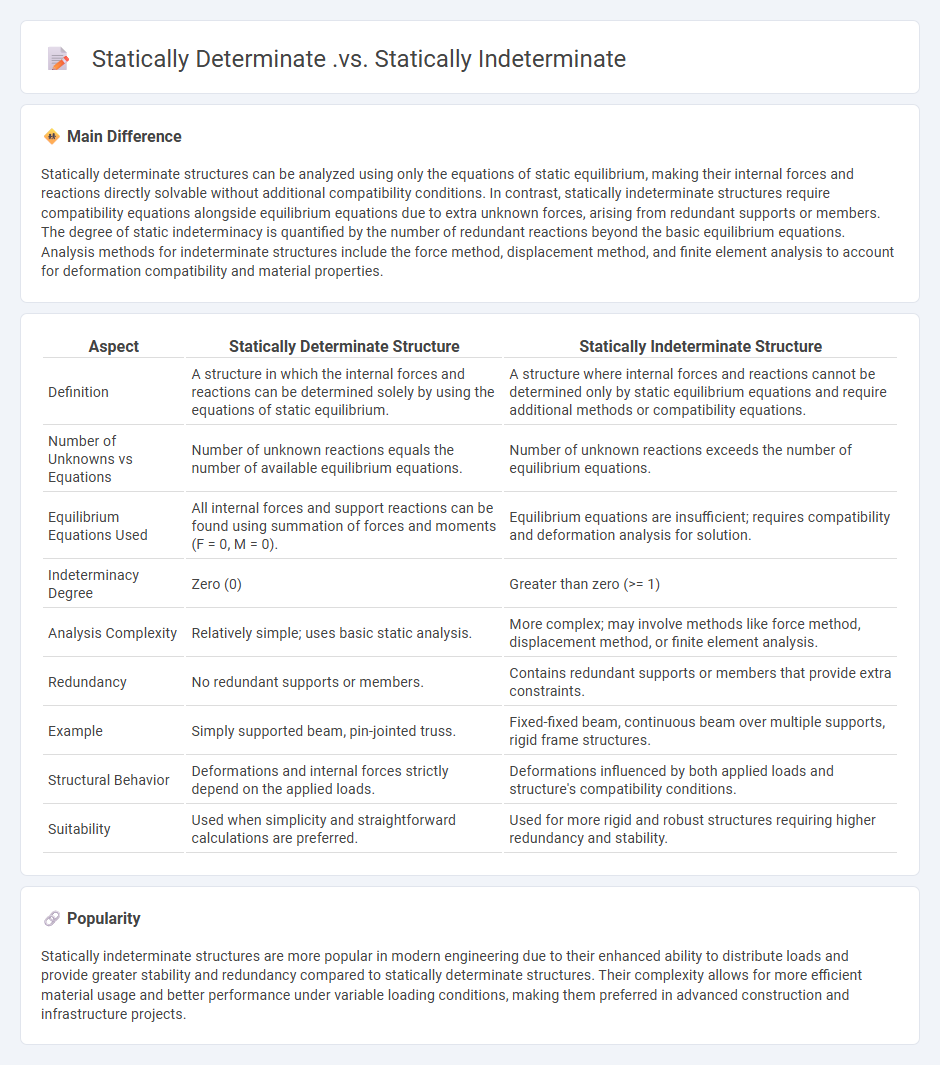
Statically determinate structures can be analyzed using only the equations of static equilibrium, making their internal forces and reactions directly solvable without additional compatibility conditions. In contrast, statically indeterminate structures require compatibility equations alongside equilibrium equations due to extra unknown forces, arising from redundant supports or members. The degree of static indeterminacy is quantified by the number of redundant reactions beyond the basic equilibrium equations. Analysis methods for indeterminate structures include the force method, displacement method, and finite element analysis to account for deformation compatibility and material properties.
Connection
Statically determinate structures can be analyzed solely using equations of static equilibrium, while statically indeterminate structures require compatibility conditions and material properties for analysis. The connection between them lies in the degree of static indeterminacy, which measures the extra constraints beyond those needed for equilibrium. Understanding this relationship helps engineers choose appropriate analysis methods based on the structure's support and member configuration.
Comparison Table
| Aspect | Statically Determinate Structure | Statically Indeterminate Structure |
|---|---|---|
| Definition | A structure in which the internal forces and reactions can be determined solely by using the equations of static equilibrium. | A structure where internal forces and reactions cannot be determined only by static equilibrium equations and require additional methods or compatibility equations. |
| Number of Unknowns vs Equations | Number of unknown reactions equals the number of available equilibrium equations. | Number of unknown reactions exceeds the number of equilibrium equations. |
| Equilibrium Equations Used | All internal forces and support reactions can be found using summation of forces and moments (F = 0, M = 0). | Equilibrium equations are insufficient; requires compatibility and deformation analysis for solution. |
| Indeterminacy Degree | Zero (0) | Greater than zero (>= 1) |
| Analysis Complexity | Relatively simple; uses basic static analysis. | More complex; may involve methods like force method, displacement method, or finite element analysis. |
| Redundancy | No redundant supports or members. | Contains redundant supports or members that provide extra constraints. |
| Example | Simply supported beam, pin-jointed truss. | Fixed-fixed beam, continuous beam over multiple supports, rigid frame structures. |
| Structural Behavior | Deformations and internal forces strictly depend on the applied loads. | Deformations influenced by both applied loads and structure's compatibility conditions. |
| Suitability | Used when simplicity and straightforward calculations are preferred. | Used for more rigid and robust structures requiring higher redundancy and stability. |
Equilibrium Equations
Equilibrium equations form the foundation of statics in engineering, ensuring that structures and mechanical systems remain stable under applied loads. These equations are derived from Newton's first law, stating that the sum of forces and moments acting on a body must be zero for it to be in equilibrium. Engineers apply equilibrium conditions in designing beams, trusses, and frames, calculating internal forces and reactions accurately to prevent structural failure. Mastery of equilibrium equations is essential for assessing safety and performance in civil, mechanical, and aerospace engineering projects.
Redundant Supports
Redundant supports in engineering enhance structural stability by providing backup load paths in case of failure. They are crucial in bridge design, aerospace structures, and critical infrastructure to ensure safety and durability. By distributing stresses more evenly, these supports reduce the risk of catastrophic collapse under unexpected loads or damage. Implementing redundant supports complies with standards such as AISC and Eurocode, optimizing both resilience and maintenance efficiency.
Internal Forces
Internal forces in engineering refer to stresses and strains that develop within a structural element due to external loads or environmental effects. These forces include tension, compression, shear, bending moments, and torsion, all critical for analyzing the stability and safety of buildings, bridges, and mechanical components. Accurate calculation of internal forces enables engineers to design structures that can withstand operational demands while minimizing material usage and costs. Finite element analysis (FEA) is a common computational tool used to model and predict internal force distributions in complex geometries.
Structural Analysis
Structural analysis in engineering involves assessing the stability, strength, and rigidity of structures such as buildings, bridges, and towers. It employs methods like finite element analysis (FEA), matrix analysis, and plastic analysis to predict structural behavior under various loads, including dead loads, live loads, wind loads, and seismic forces. Advanced software tools like SAP2000, ANSYS, and STAAD.Pro enable precise modeling and simulation, enhancing design safety and efficiency. Accurate structural analysis ensures compliance with international standards like Eurocode, AISC, and ASCE 7, minimizing risks of failure and optimizing material use.
Degree of Indeterminacy
Degree of indeterminacy in engineering refers to the number of unknown forces or reactions in a structure that cannot be determined solely by equilibrium equations. It quantifies the extent to which a structural system is statically indeterminate, requiring compatibility equations or advanced analysis methods for resolution. Structures with a high degree of indeterminacy often exhibit increased redundancy, enhancing load distribution and resilience against component failures. Calculating this degree is essential in structural analysis to ensure safety, optimize material usage, and predict deflections accurately.
Source and External Links
Statically Determinate & Indeterminate Structures - Explains the difference between statically determinate structures, where reaction forces and internal forces can be calculated using equilibrium equations, and indeterminate structures, which require more complex methods.
Determinate vs Indeterminate Structures - Discusses how determinate structures have solvable unknowns using equilibrium equations, while indeterminate structures require additional equations.
Statical Determinacy and Indeterminacy Of Structures - Covers the concept of statically determinate structures and how they differ from indeterminate ones, focusing on beams and frames.
FAQs
What does statically determinate mean?
Statically determinate means a structure or system where internal forces and reactions can be calculated solely using equilibrium equations without additional compatibility or material behavior equations.
What is statically indeterminate in structural analysis?
A statically indeterminate structure is one where the static equilibrium equations alone are insufficient to determine internal forces and reactions due to extra supports or redundancies.
How do you identify a statically determinate structure?
A statically determinate structure is identified when the number of unknown reactions equals the number of independent static equilibrium equations available for analysis.
Why are some structures statically indeterminate?
Some structures are statically indeterminate because their internal forces and reactions cannot be determined from static equilibrium equations alone due to redundant supports or members.
What are the advantages of statically determinate structures?
Statically determinate structures offer advantages such as simpler analysis using only equilibrium equations, predictable behavior under load, easier detection of errors, reduced computational effort, and straightforward design verification.
What challenges are faced with statically indeterminate structures?
Statically indeterminate structures face challenges such as complex internal force analysis, requirement of compatibility equations, sensitivity to material properties and support conditions, difficulty in predicting deflections, and increased computational effort for accurate solutions.
How do you analyze statically indeterminate systems?
Analyze statically indeterminate systems using compatibility equations combined with equilibrium equations, applying methods like the force method, displacement method (such as the moment distribution method and finite element analysis), and superposition to solve for unknown redundants and internal forces.
 calledges.com
calledges.com