Breadth-First Search (BFS) explores graph nodes level by level, making it efficient for finding the shortest path in unweighted graphs, while Depth-First Search (DFS) dives deep into each branch before backtracking, which is useful for pathfinding and detecting cycles. Both algorithms use distinct data structures: BFS employs a queue, whereas DFS utilizes a stack or recursion to traverse nodes. Discover how BFS and DFS algorithms differ in performance and application across various graph problems.
Main Difference
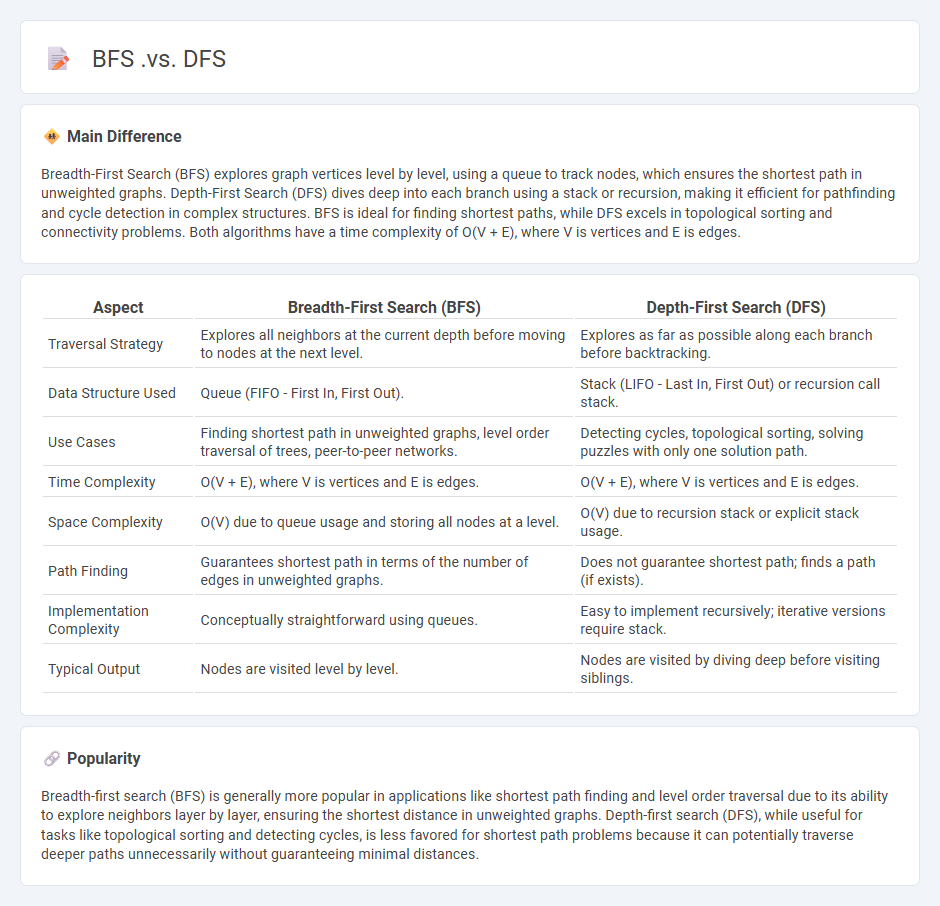
Breadth-First Search (BFS) explores graph vertices level by level, using a queue to track nodes, which ensures the shortest path in unweighted graphs. Depth-First Search (DFS) dives deep into each branch using a stack or recursion, making it efficient for pathfinding and cycle detection in complex structures. BFS is ideal for finding shortest paths, while DFS excels in topological sorting and connectivity problems. Both algorithms have a time complexity of O(V + E), where V is vertices and E is edges.
Connection
Breadth-First Search (BFS) and Depth-First Search (DFS) are both fundamental graph traversal algorithms used to explore nodes systematically. BFS explores neighbors level by level using a queue, enabling shortest path detection in unweighted graphs, while DFS uses a stack or recursion to traverse deeper paths first, aiding in cycle detection and topological sorting. Their connection lies in their systematic approach to visiting nodes, differing mainly in data structures and traversal order, making them complementary for various graph-related problems.
Comparison Table
| Aspect | Breadth-First Search (BFS) | Depth-First Search (DFS) |
|---|---|---|
| Traversal Strategy | Explores all neighbors at the current depth before moving to nodes at the next level. | Explores as far as possible along each branch before backtracking. |
| Data Structure Used | Queue (FIFO - First In, First Out). | Stack (LIFO - Last In, First Out) or recursion call stack. |
| Use Cases | Finding shortest path in unweighted graphs, level order traversal of trees, peer-to-peer networks. | Detecting cycles, topological sorting, solving puzzles with only one solution path. |
| Time Complexity | O(V + E), where V is vertices and E is edges. | O(V + E), where V is vertices and E is edges. |
| Space Complexity | O(V) due to queue usage and storing all nodes at a level. | O(V) due to recursion stack or explicit stack usage. |
| Path Finding | Guarantees shortest path in terms of the number of edges in unweighted graphs. | Does not guarantee shortest path; finds a path (if exists). |
| Implementation Complexity | Conceptually straightforward using queues. | Easy to implement recursively; iterative versions require stack. |
| Typical Output | Nodes are visited level by level. | Nodes are visited by diving deep before visiting siblings. |
Traversal Order
Traversal order in computer science refers to the sequence in which nodes or elements of data structures like trees or graphs are visited. Common traversal methods include depth-first search (DFS) and breadth-first search (BFS), each serving different algorithmic purposes. In binary trees, traversal orders include pre-order, in-order, and post-order, crucial for tasks such as expression evaluation and tree reconstruction. Efficient traversal order selection impacts the performance of search, sort, and graph algorithms in applications ranging from database indexing to artificial intelligence.
Data Structure (Queue vs Stack)
Queues and stacks are fundamental data structures used in computer science to manage collections of elements. A queue operates on a First-In-First-Out (FIFO) principle, where elements are added at the rear and removed from the front, making it ideal for scheduling tasks and breadth-first search algorithms. A stack follows a Last-In-First-Out (LIFO) approach, with elements pushed and popped from the top, commonly used in function call management and depth-first search. Both structures optimize data handling by enforcing specific access patterns essential for algorithm efficiency and memory management.
Memory Usage
Memory usage in computers refers to the amount of RAM (Random Access Memory) actively utilized by programs and operating system processes. Efficient memory management is crucial for system performance, as high memory usage can lead to slow processing speeds and increased paging or swapping to disk. Modern operating systems like Windows 11 and macOS monitor memory allocation dynamically to optimize multitasking and reduce latency. Tools such as Task Manager on Windows or Activity Monitor on macOS provide detailed insights into real-time memory consumption by individual applications and system services.
Path Finding
Path finding in computer science is a critical algorithmic process used to determine the shortest or most efficient route between two nodes in a graph or network. Common algorithms such as Dijkstra's, A*, and Bellman-Ford optimize path selection by evaluating cost, distance, and heuristic information. Applications span from robotics navigation and geographic information systems (GIS) to game development and network routing protocols. Efficient path finding enhances computational performance and accuracy in real-time systems and large-scale data environments.
Completeness and Optimality
Completeness in computer science refers to an algorithm's ability to find a solution if one exists within the search space. Optimality ensures that the solution found is the best according to a defined cost function or criteria, such as shortest path or minimal resource usage. These properties are critical in fields like artificial intelligence, particularly in search algorithms like A* and Dijkstra's, where finding the most efficient solution is vital. Ensuring both completeness and optimality often involves trade-offs between computational time and resource consumption.
Source and External Links
Difference between BFS and DFS - Tutorials Point - BFS uses a queue and explores nodes level by level to find the shortest path, while DFS uses a stack to explore as deep as possible along a branch before backtracking; BFS requires more memory but avoids infinite loops, whereas DFS uses less memory but can get trapped in loops.
Difference between BFS and DFS - GeeksforGeeks - BFS traverses the graph layer-wise and is suitable for finding vertices close to the source using FIFO queue, whereas DFS explores graph depth-wise with a LIFO stack, making it better for cases where solutions are far from the source, both having O(V+E) time complexity.
Breadth-First Search vs Depth-First Search: Key Differences - Codecademy - BFS is ideal for shortest path discovery in unweighted graphs using a queue for layer-by-layer exploration, while DFS is more memory-efficient and better when the path target is deep in the graph, implemented using a stack.
FAQs
What is Breadth First Search BFS?
Breadth First Search (BFS) is a graph traversal algorithm that explores vertices level by level, starting from a source node and visiting all its neighbors before moving to the next level of nodes.
What is Depth First Search DFS?
Depth First Search (DFS) is a graph traversal algorithm that explores vertices by moving as deep as possible along each branch before backtracking.
What are the key differences between BFS and DFS?
BFS explores nodes level by level using a queue, ensuring the shortest path in unweighted graphs, while DFS explores as deep as possible along each branch using a stack or recursion, enabling pathfinding and topological sorting but not guaranteeing shortest paths.
When should you use BFS over DFS?
Use BFS over DFS when you need the shortest path in unweighted graphs, want to explore nodes level by level, or when searching for the closest target.
What are the advantages of BFS?
BFS guarantees the shortest path in unweighted graphs, explores nodes level by level, efficiently finds connected components, and is suitable for shortest path and minimum spanning tree problems in unweighted graphs.
What are the disadvantages of DFS?
DFS may get stuck in deep or infinite branches, lacks optimality and completeness in infinite spaces, and uses more memory in worst-case scenarios compared to BFS.
How do BFS and DFS impact algorithm efficiency?
BFS efficiently finds shortest paths in unweighted graphs with O(V + E) time complexity, while DFS uses O(V + E) time but may explore deeper paths, impacting memory use and search order.
 calledges.com
calledges.com