Breadth-First Search (BFS) explores a graph level by level, using a queue to visit all nodes at the current depth before moving deeper. Depth-First Search (DFS) dives into each branch of the graph as far as possible, employing a stack or recursion to traverse nodes. Explore the detailed comparison to understand their applications and efficiency in graph traversal.
Main Difference
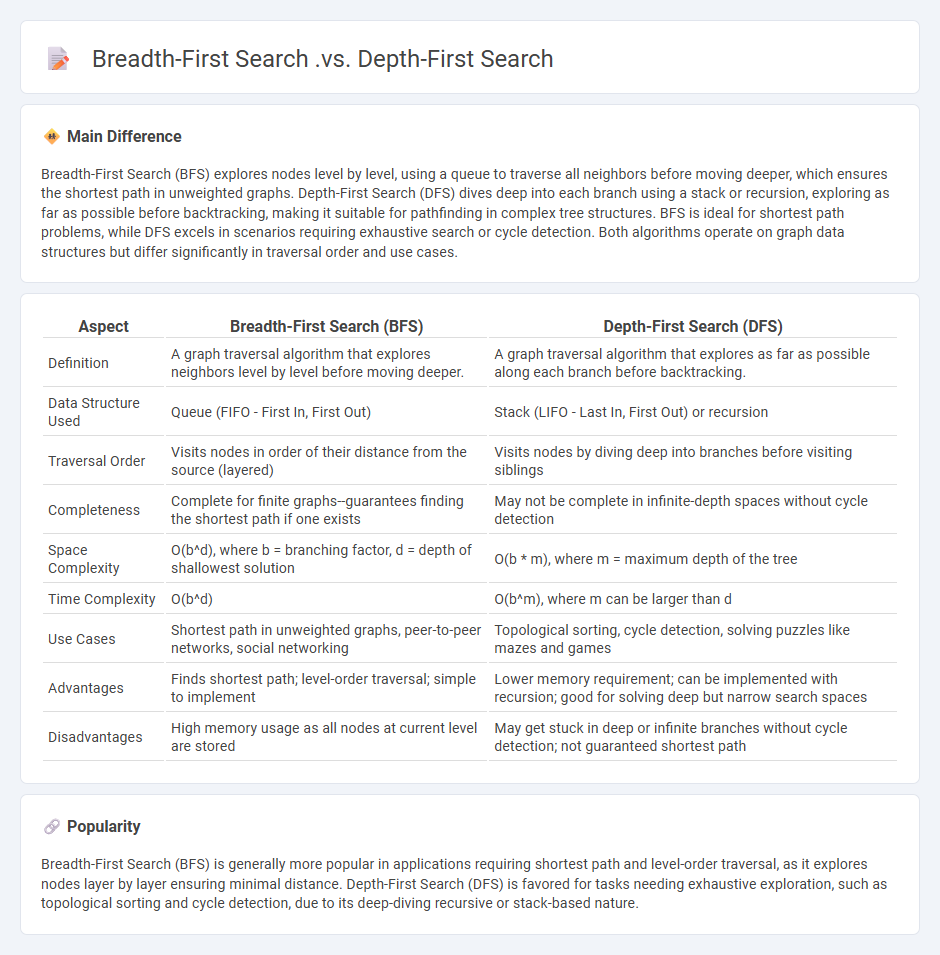
Breadth-First Search (BFS) explores nodes level by level, using a queue to traverse all neighbors before moving deeper, which ensures the shortest path in unweighted graphs. Depth-First Search (DFS) dives deep into each branch using a stack or recursion, exploring as far as possible before backtracking, making it suitable for pathfinding in complex tree structures. BFS is ideal for shortest path problems, while DFS excels in scenarios requiring exhaustive search or cycle detection. Both algorithms operate on graph data structures but differ significantly in traversal order and use cases.
Connection
Breadth-First Search (BFS) and Depth-First Search (DFS) are both graph traversal algorithms used to explore nodes and edges systematically, differing primarily in the order of node exploration. BFS uses a queue data structure to explore neighbors level by level, ensuring the shortest path in unweighted graphs, while DFS employs a stack or recursion to explore as far along a branch as possible before backtracking. Both algorithms serve foundational roles in solving problems such as pathfinding, cycle detection, and connectivity analysis in graph theory.
Comparison Table
| Aspect | Breadth-First Search (BFS) | Depth-First Search (DFS) |
|---|---|---|
| Definition | A graph traversal algorithm that explores neighbors level by level before moving deeper. | A graph traversal algorithm that explores as far as possible along each branch before backtracking. |
| Data Structure Used | Queue (FIFO - First In, First Out) | Stack (LIFO - Last In, First Out) or recursion |
| Traversal Order | Visits nodes in order of their distance from the source (layered) | Visits nodes by diving deep into branches before visiting siblings |
| Completeness | Complete for finite graphs--guarantees finding the shortest path if one exists | May not be complete in infinite-depth spaces without cycle detection |
| Space Complexity | O(b^d), where b = branching factor, d = depth of shallowest solution | O(b * m), where m = maximum depth of the tree |
| Time Complexity | O(b^d) | O(b^m), where m can be larger than d |
| Use Cases | Shortest path in unweighted graphs, peer-to-peer networks, social networking | Topological sorting, cycle detection, solving puzzles like mazes and games |
| Advantages | Finds shortest path; level-order traversal; simple to implement | Lower memory requirement; can be implemented with recursion; good for solving deep but narrow search spaces |
| Disadvantages | High memory usage as all nodes at current level are stored | May get stuck in deep or infinite branches without cycle detection; not guaranteed shortest path |
Traversal Order
Traversal order in computer science refers to the specific sequence in which nodes or elements of a data structure, such as trees or graphs, are visited and processed. Common traversal methods include depth-first search (DFS) and breadth-first search (BFS), with DFS encompassing pre-order, in-order, and post-order techniques for binary trees. In-order traversal visits the left subtree, root node, and then the right subtree, often used in binary search trees to retrieve sorted data. BFS explores all nodes at the present depth level before moving to the nodes at the next depth level, suitable for shortest path algorithms in unweighted graphs.
Data Structure (Queue vs Stack)
A queue is a linear data structure that follows the First-In-First-Out (FIFO) principle, where elements are inserted at the rear and removed from the front, making it ideal for scheduling tasks and managing resource sharing in computer systems. A stack operates on the Last-In-First-Out (LIFO) principle, with elements added and removed from the top, commonly used for function call management, expression evaluation, and backtracking algorithms. Both data structures are fundamental in computer science, enabling efficient memory management and algorithm implementation. The choice between a queue and stack depends on the specific problem requirements, such as order processing or hierarchical data traversal.
Time and Space Complexity
Time complexity measures the amount of computational time an algorithm takes relative to its input size, typically expressed using Big O notation such as O(n), O(log n), or O(n2). Space complexity evaluates the amount of memory an algorithm requires during its execution, also represented by Big O notation to indicate how memory usage scales with input size. Efficient algorithms strive to minimize both time and space complexity to optimize performance, especially important in large-scale computing and resource-constrained environments. Common examples include sorting algorithms like QuickSort with average time complexity O(n log n) and space complexity O(log n).
Pathfinding and Completeness
Pathfinding algorithms in computer science focus on determining the shortest or most efficient path between nodes in graphs or networks. Completeness in pathfinding ensures that an algorithm is guaranteed to find a solution if one exists, which is critical in applications like robotics, gaming, and geographic information systems. Common algorithms such as A*, Dijkstra's, and Breadth-First Search demonstrate varying degrees of completeness depending on graph topology and heuristic accuracy. The choice of algorithm impacts computational efficiency, memory usage, and solution optimality in complex environments.
Use Cases (Shortest Path, Cycle Detection, etc.)
Shortest path algorithms like Dijkstra's and A* are essential in computer networks for efficient routing and data packet delivery. Cycle detection methods, such as depth-first search, help in identifying loops in graphs, crucial for optimizing processes and preventing infinite loops in workflows. These algorithms are applied in various domains, including social network analysis, GPS navigation, and compiler optimization. Graph theory underpins many computational problems, enabling optimized solutions in systems design and artificial intelligence.
Source and External Links
Breadth-First Search vs Depth-First Search: Key Differences - This article compares Breadth-First Search (BFS) and Depth-First Search (DFS) in terms of their use cases, data structures, and efficiency for graph traversal.
Difference between BFS and DFS - This resource outlines the differences between BFS and DFS, highlighting their suitable applications and data structures used.
Breadth First vs Depth First Search - This post discusses the basics and contrast of BFS and DFS, focusing on their traversal methods and optimal use cases.
 calledges.com
calledges.com