Stochastic dominance and mean-variance dominance are key concepts in decision theory and portfolio optimization, offering distinct criteria for comparing uncertain prospects. While stochastic dominance provides a hierarchy based on entire distribution functions, mean-variance dominance simplifies comparisons using only the first two moments of returns--mean and variance. Explore these frameworks deeply to enhance your understanding of risk assessment and investment choice.
Main Difference
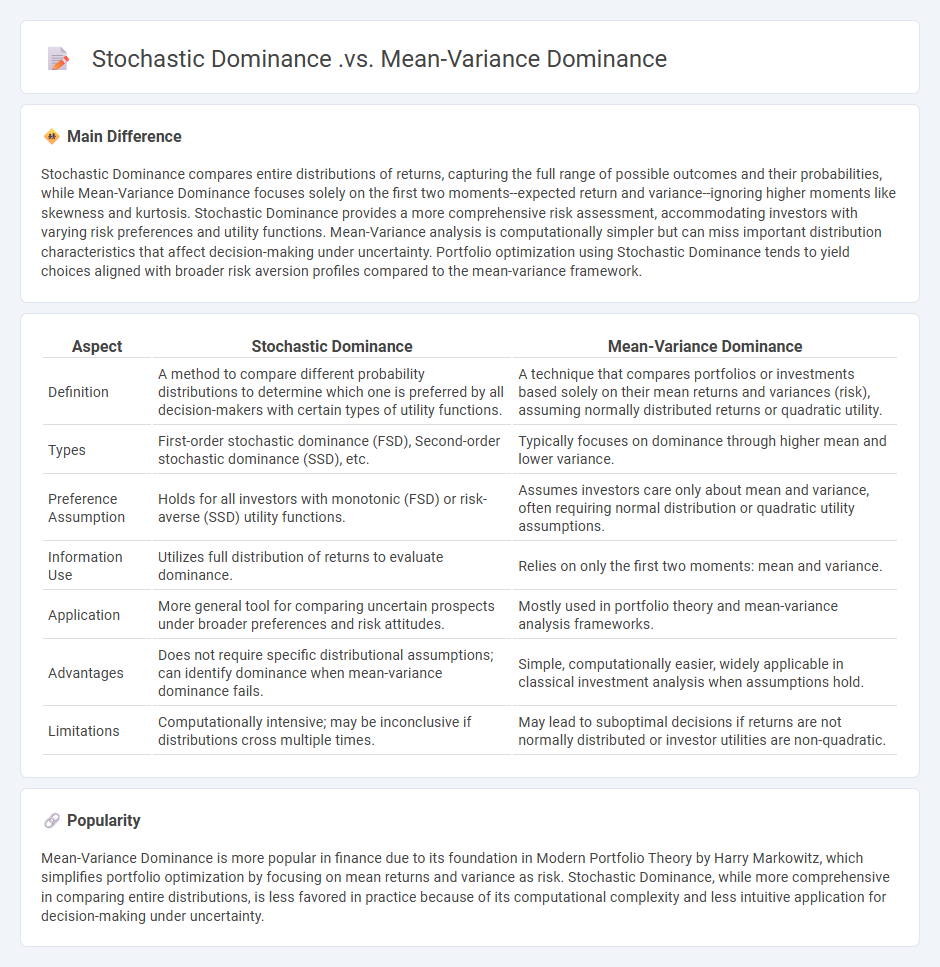
Stochastic Dominance compares entire distributions of returns, capturing the full range of possible outcomes and their probabilities, while Mean-Variance Dominance focuses solely on the first two moments--expected return and variance--ignoring higher moments like skewness and kurtosis. Stochastic Dominance provides a more comprehensive risk assessment, accommodating investors with varying risk preferences and utility functions. Mean-Variance analysis is computationally simpler but can miss important distribution characteristics that affect decision-making under uncertainty. Portfolio optimization using Stochastic Dominance tends to yield choices aligned with broader risk aversion profiles compared to the mean-variance framework.
Connection
Stochastic dominance and mean-variance dominance both serve as criteria for comparing investment opportunities based on different preference frameworks. Stochastic dominance provides a more general condition by comparing entire distributions of returns, while mean-variance dominance simplifies this by focusing only on the first two moments: expected return and variance. Investors who prefer higher expected returns and lower risk often rely on mean-variance dominance, which is a special case of stochastic dominance under specific assumptions like normally distributed returns or quadratic utility functions.
Comparison Table
| Aspect | Stochastic Dominance | Mean-Variance Dominance |
|---|---|---|
| Definition | A method to compare different probability distributions to determine which one is preferred by all decision-makers with certain types of utility functions. | A technique that compares portfolios or investments based solely on their mean returns and variances (risk), assuming normally distributed returns or quadratic utility. |
| Types | First-order stochastic dominance (FSD), Second-order stochastic dominance (SSD), etc. | Typically focuses on dominance through higher mean and lower variance. |
| Preference Assumption | Holds for all investors with monotonic (FSD) or risk-averse (SSD) utility functions. | Assumes investors care only about mean and variance, often requiring normal distribution or quadratic utility assumptions. |
| Information Use | Utilizes full distribution of returns to evaluate dominance. | Relies on only the first two moments: mean and variance. |
| Application | More general tool for comparing uncertain prospects under broader preferences and risk attitudes. | Mostly used in portfolio theory and mean-variance analysis frameworks. |
| Advantages | Does not require specific distributional assumptions; can identify dominance when mean-variance dominance fails. | Simple, computationally easier, widely applicable in classical investment analysis when assumptions hold. |
| Limitations | Computationally intensive; may be inconclusive if distributions cross multiple times. | May lead to suboptimal decisions if returns are not normally distributed or investor utilities are non-quadratic. |
Risk Preferences
Risk preferences in economics describe how individuals or firms evaluate uncertain outcomes involving potential gains or losses, influencing their decision-making processes. These preferences are typically modeled using utility functions, such as expected utility theory, which captures attitudes toward risk as risk-averse, risk-neutral, or risk-seeking. Empirical studies often use prospect theory to better explain observed behaviors that deviate from expected utility, emphasizing loss aversion and probability weighting. Quantifying risk preferences is critical in financial markets, insurance, and behavioral economics to predict choices under uncertainty and design effective policies.
Utility Functions
Utility functions quantify individual preferences in economics by assigning numerical values to different bundles of goods or outcomes to represent satisfaction levels. They serve as foundational tools for modeling consumer choice, enabling the prediction of demand behavior under constraints like budget limits. Common forms include Cobb-Douglas, CES (constant elasticity of substitution), and quasi-linear utility functions, each capturing different substitution effects between goods. Utility maximization subject to budget constraints leads to demand functions, facilitating welfare analysis and policy evaluation in microeconomic theory.
Portfolio Optimization
Portfolio optimization in economics involves selecting the best mix of assets to maximize returns while minimizing risk, based on the principles of modern portfolio theory developed by Harry Markowitz in 1952. It uses quantitative methods, such as mean-variance optimization, to balance expected returns against portfolio variance, ensuring an efficient frontier of optimal portfolios. Financial tools like the Capital Asset Pricing Model (CAPM) and the Sharpe ratio further refine asset selection by assessing risk-adjusted performance. This optimization is essential for investors and fund managers aiming to achieve strategic asset allocation aligned with specific risk tolerance and investment goals.
Distribution Assumptions
Distribution assumptions in economics refer to the theoretical premises about how income, wealth, and resources are allocated among individuals and groups within an economy. These assumptions are critical for modeling market behavior, determining equilibrium outcomes, and analyzing economic inequality. Common distribution assumptions include perfect competition, equal bargaining power, and rational behavior, which influence predictions about wage distribution, capital returns, and consumer spending. Empirical studies often challenge these assumptions by highlighting disparities caused by market imperfections, policy interventions, and social factors.
Decision Criteria
Decision criteria in economics refer to the quantitative and qualitative benchmarks used to evaluate the feasibility and desirability of various economic choices. Common criteria include cost-benefit analysis, utility maximization, risk assessment, and return on investment, which help in selecting the most efficient allocation of resources. Firms often rely on marginal analysis to determine the optimal level of production where marginal cost equals marginal revenue. Governments utilize these criteria when implementing policies to maximize social welfare and economic efficiency.
Source and External Links
Mean-variance versus stochastic dominance - Stochastic dominance compares entire return distributions and captures risk features beyond mean-variance metrics, often penalizing high volatility investments with negative skewness, whereas mean-variance focuses only on the first two moments (mean and variance) of returns, leading to different investment rankings and indicating that stochastic dominance provides a more comprehensive risk evaluation tool.
Comparing mean variance tests with stochastic dominance tests - Stochastic dominance theory is superior to mean-variance analysis because it considers the entire return distribution and minimal assumptions about investor preferences, with first-order stochastic dominance implying second- and third-order dominance, while mean-variance relies on means and variances only, limiting its applicability when distributions are non-normal or skewed.
Comparing Mean Variance Tests with Stochastic Dominance When Assessing International Portfolio Diversification Benefits - Stochastic dominance tests provide a more robust framework than mean-variance by fully capturing distributional differences across portfolios, often producing findings discordant with those from mean-variance analysis, especially during market stress periods, thus offering advantages for portfolio evaluation and diversification assessment.
FAQs
What is stochastic dominance?
Stochastic dominance is a statistical method used to compare probability distributions, determining if one distribution consistently yields higher values than another across a range of outcomes.
What is mean-variance dominance?
Mean-variance dominance occurs when one investment's expected return (mean) is higher and its risk (variance) is lower than another investment, making it preferable under mean-variance analysis.
How do stochastic dominance and mean-variance dominance differ?
Stochastic dominance compares entire probability distributions based on cumulative distribution functions for risk-averse decision-making, while mean-variance dominance evaluates alternatives solely by their expected returns (mean) and risk (variance), ignoring distribution shape beyond the first two moments.
What are the assumptions behind stochastic dominance?
Stochastic dominance assumes a complete and transitive preference ordering over uncertain prospects, consistent risk-averse decision-making, known probability distributions of outcomes, and that preferences satisfy monotonicity and continuity.
When is mean-variance dominance preferred in decision-making?
Mean-variance dominance is preferred in decision-making when assessing investments or choices under uncertainty where only the first two moments (mean and variance) of the payoff distributions are known or relevant, particularly in financial portfolio selection and risk management.
How are these dominance criteria used in portfolio selection?
Dominance criteria in portfolio selection prioritize assets or portfolios that outperform others based on risk-return trade-offs, enabling investors to eliminate dominated options and focus on efficient frontiers for optimal asset allocation.
What are the limitations of stochastic and mean-variance dominance?
Stochastic dominance is limited by its reliance on complete preference ordering and may fail to rank options when distributions intersect; mean-variance dominance is constrained by its assumption of normally distributed returns and quadratic utility, making it inadequate for non-normal or skewed risk profiles.
 calledges.com
calledges.com