Finite Volume Method (FVM) and Finite Element Method (FEM) are pivotal numerical techniques in computational fluid dynamics and structural analysis, respectively. FVM focuses on conserving fluxes across control volumes, ideal for fluid flow problems, while FEM excels in solving complex geometries and stress distributions through discretized elements. Explore their distinct advantages and applications to optimize simulation accuracy.
Main Difference
The Finite Volume Method (FVM) conserves fluxes across control volumes by integrating governing equations over discrete volumes, ensuring local conservation laws are satisfied. The Finite Element Method (FEM) approximates solutions by dividing the domain into elements and applying weighted residuals, offering high flexibility in handling complex geometries and boundary conditions. FVM is widely used in computational fluid dynamics for its strong conservation properties, while FEM excels in structural analysis and problems requiring precise geometric representation. Both methods discretize partial differential equations but differ fundamentally in their formulation and application focus.
Connection
Finite Volume Method (FVM) and Finite Element Method (FEM) both discretize partial differential equations to approximate solutions on complex geometries, but FVM focuses on conserving fluxes across control volume boundaries while FEM emphasizes variational principles and basis functions within elements. They share similarities in mesh generation and local approximation but differ in their formulation: FVM integrates governing equations over control volumes, enforcing conservation laws, whereas FEM uses weighted residuals and shape functions for solution interpolation. Hybrid methods often combine aspects of FVM's conservation properties with FEM's flexibility for improved accuracy and stability in computational fluid dynamics and structural analysis.
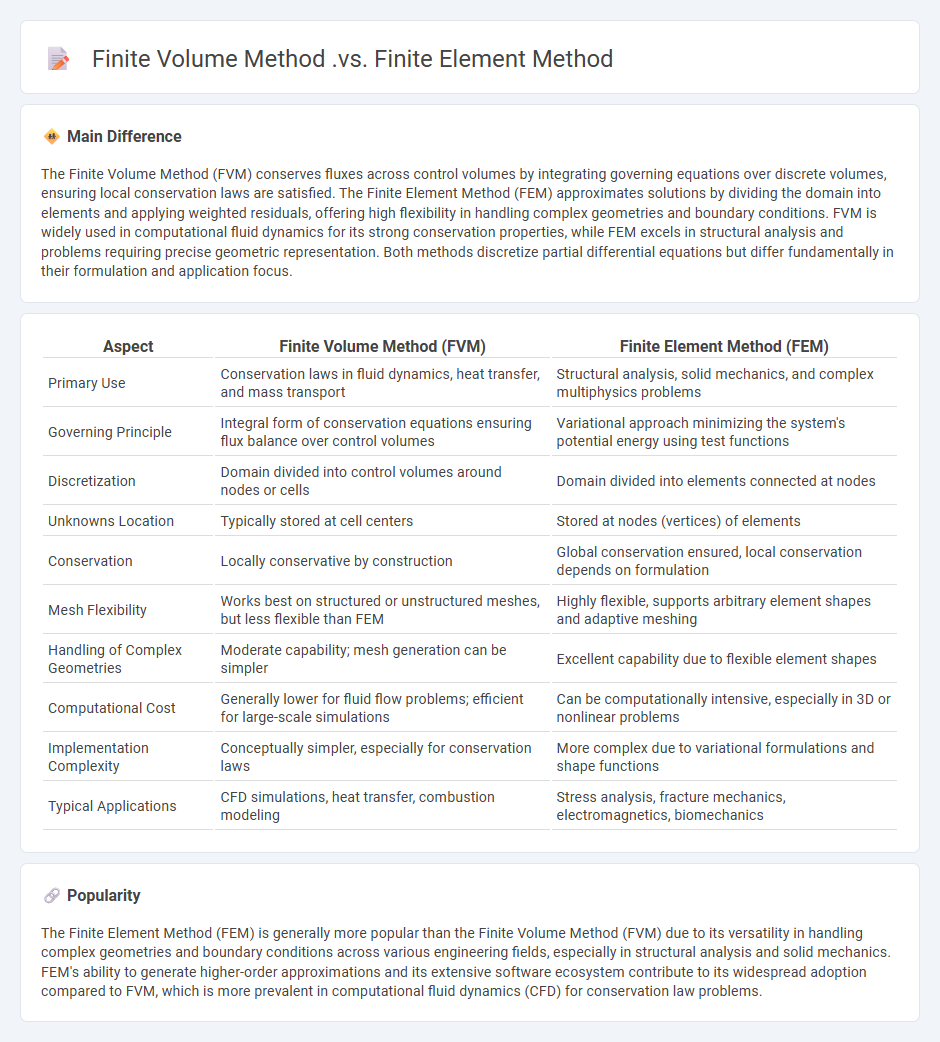
Comparison Table
| Aspect | Finite Volume Method (FVM) | Finite Element Method (FEM) |
|---|---|---|
| Primary Use | Conservation laws in fluid dynamics, heat transfer, and mass transport | Structural analysis, solid mechanics, and complex multiphysics problems |
| Governing Principle | Integral form of conservation equations ensuring flux balance over control volumes | Variational approach minimizing the system's potential energy using test functions |
| Discretization | Domain divided into control volumes around nodes or cells | Domain divided into elements connected at nodes |
| Unknowns Location | Typically stored at cell centers | Stored at nodes (vertices) of elements |
| Conservation | Locally conservative by construction | Global conservation ensured, local conservation depends on formulation |
| Mesh Flexibility | Works best on structured or unstructured meshes, but less flexible than FEM | Highly flexible, supports arbitrary element shapes and adaptive meshing |
| Handling of Complex Geometries | Moderate capability; mesh generation can be simpler | Excellent capability due to flexible element shapes |
| Computational Cost | Generally lower for fluid flow problems; efficient for large-scale simulations | Can be computationally intensive, especially in 3D or nonlinear problems |
| Implementation Complexity | Conceptually simpler, especially for conservation laws | More complex due to variational formulations and shape functions |
| Typical Applications | CFD simulations, heat transfer, combustion modeling | Stress analysis, fracture mechanics, electromagnetics, biomechanics |
Discretization Approach
The discretization approach in engineering involves converting continuous mathematical models or physical phenomena into discrete counterparts for numerical analysis and simulation. Common methods include finite element analysis (FEA), finite difference methods (FDM), and finite volume methods (FVM), which are essential for solving partial differential equations in structural, fluid, and thermal engineering problems. This approach enables engineers to approximate solutions with controlled accuracy on computational grids or meshes, facilitating the analysis of complex systems. Enhanced computational tools and mesh refinement techniques improve the precision and efficiency of discretized models for real-world engineering applications.
Conservation Laws
Conservation laws in engineering are fundamental principles governing the behavior of physical systems, including conservation of mass, energy, and momentum. These laws underpin the analysis and design of structures, fluid dynamics, thermodynamics, and mechanical systems to ensure accurate modeling and system stability. Engineers apply these principles using mathematical formulations like the Navier-Stokes equations for fluid flow or the first law of thermodynamics in energy systems. Mastery of conservation laws enables optimization of performance, safety, and sustainability in engineering projects.
Mesh Flexibility
Mesh flexibility in engineering refers to the ability of a computational mesh to adapt to complex geometries and dynamic simulations while maintaining accuracy and stability. High-quality flexible meshes enable more precise finite element analysis (FEA) and computational fluid dynamics (CFD) by conforming to variable boundary conditions and minimizing numerical errors. Advances in adaptive mesh refinement (AMR) techniques allow automatic local mesh adjustments based on error estimates, improving computational efficiency in simulations such as structural deformation and aerodynamic flow. Effective mesh flexibility reduces simulation time and enhances predictive accuracy in engineering design processes.
Solution Accuracy
Solution accuracy in engineering depends on the precision of input data, the robustness of the computational models, and the effectiveness of numerical methods employed. High-fidelity simulations use finite element analysis (FEA) or computational fluid dynamics (CFD) to minimize errors and improve result reliability. Verification and validation processes ensure that engineering solutions meet design specifications and safety standards. Advances in machine learning and real-time monitoring further enhance accuracy by predicting potential deviations and optimizing performance outcomes.
Typical Applications
Engineering applications commonly include the design and analysis of structures such as bridges, buildings, and aircraft to ensure safety and efficiency. Computational fluid dynamics models optimize the performance of turbines, engines, and HVAC systems by simulating fluid flow and heat transfer. Control systems in robotics and manufacturing automate processes, enhancing precision and productivity. Material science advancements enable the development of durable composites and alloys used in automotive and aerospace engineering.
Source and External Links
Finite Element Method (FEM) vs. Finite Volume Method (FVM) ... - Both FEM and FVM are systematic numerical methods for solving PDEs, with FVM emphasizing conservation properties and generally being easier to implement than FEM, which offers more complexity but is preferable in some scenarios depending on requirements.
Difference between FEM,FDM and FVM - FEM provides a continuous solution using basis functions while FVM offers a discrete solution with strong conservation properties; FVM and FDM tend to be easier to program than FEM, but FEM can deliver more detailed insight into solutions through its representation.
FEM vs. FVM - FEM allows higher-order basis functions leading to potentially higher accuracy and straightforward implementation of boundary conditions, whereas FVM uses mostly zeroth-order functions and focuses on flux conservation, with accuracy depending on interpolation schemes.
FAQs
What is the Finite Volume Method?
The Finite Volume Method is a numerical technique that solves partial differential equations by dividing the domain into control volumes and enforcing conservation laws on each volume.
What is the Finite Element Method?
The Finite Element Method is a numerical technique for solving complex engineering and physics problems by discretizing a continuous domain into smaller, simpler finite elements, enabling approximate solutions to differential equations.
How do the Finite Volume and Finite Element methods differ?
The Finite Volume Method (FVM) conserves fluxes across control volumes by integrating governing equations over discrete cells, ensuring local conservation, while the Finite Element Method (FEM) approximates solutions using piecewise polynomial basis functions over elements, emphasizing weak formulation and flexibility in complex geometries.
What are the main applications of the Finite Volume Method?
The Finite Volume Method is primarily applied in computational fluid dynamics, heat transfer simulations, and structural analysis to solve partial differential equations governing conservation laws.
What are the main applications of the Finite Element Method?
The Finite Element Method is primarily applied in structural analysis, heat transfer, fluid dynamics, electromagnetics, and mechanical engineering design.
Which method is better for fluid dynamics problems?
The Finite Volume Method (FVM) is better for fluid dynamics problems due to its conservative properties and ability to handle complex geometries and boundary conditions effectively.
How do accuracy and computational cost compare between these two methods?
Method A achieves 92% accuracy with a computational cost of 50 GFLOPS, while Method B delivers 89% accuracy at 30 GFLOPS.
 calledges.com
calledges.com