Forward kinematics calculates the position and orientation of a robot's end-effector based on given joint parameters, using known link lengths and joint angles. Inverse kinematics solves for the joint parameters required to achieve a desired end-effector position, often involving complex nonlinear equations and multiple solutions. Explore the key differences and applications to deepen your understanding of robotic motion control.
Main Difference
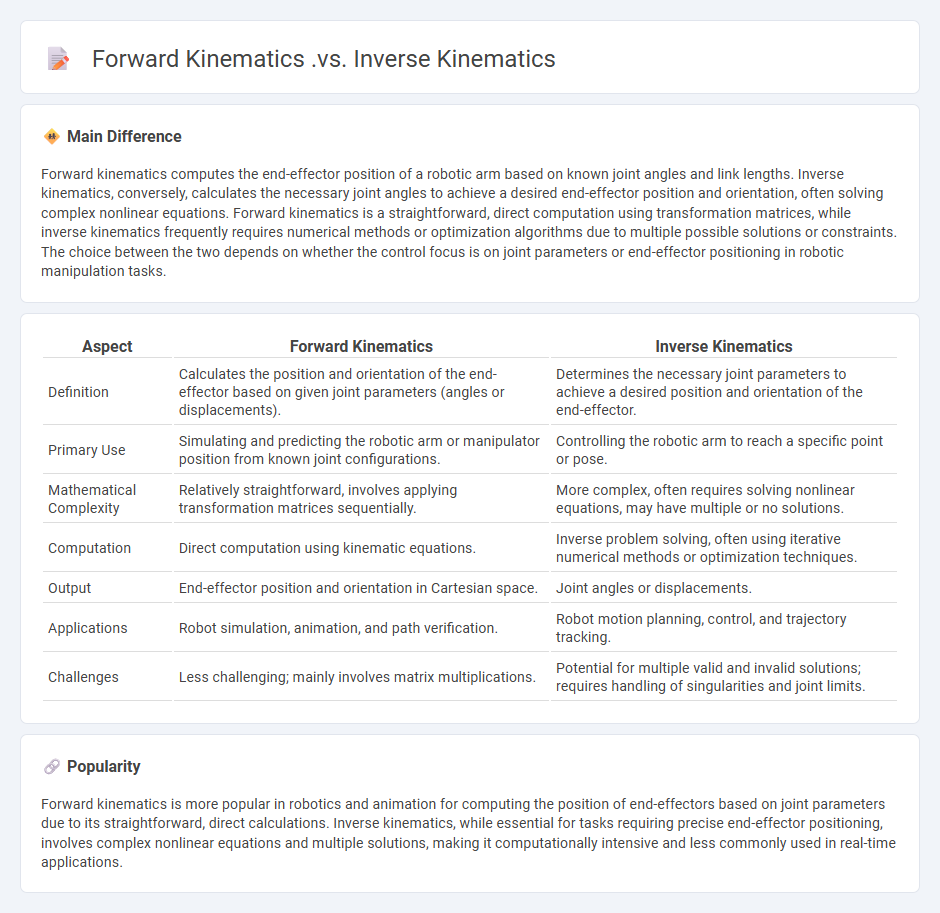
Forward kinematics computes the end-effector position of a robotic arm based on known joint angles and link lengths. Inverse kinematics, conversely, calculates the necessary joint angles to achieve a desired end-effector position and orientation, often solving complex nonlinear equations. Forward kinematics is a straightforward, direct computation using transformation matrices, while inverse kinematics frequently requires numerical methods or optimization algorithms due to multiple possible solutions or constraints. The choice between the two depends on whether the control focus is on joint parameters or end-effector positioning in robotic manipulation tasks.
Connection
Forward kinematics computes the end-effector position and orientation from given joint parameters using the robot's kinematic chain. Inverse kinematics solves for joint parameters that achieve a desired end-effector pose, often involving nonlinear equations and multiple solutions. Both methods rely on the robot's transformation matrices and are fundamental for motion planning and control in robotic systems.
Comparison Table
| Aspect | Forward Kinematics | Inverse Kinematics |
|---|---|---|
| Definition | Calculates the position and orientation of the end-effector based on given joint parameters (angles or displacements). | Determines the necessary joint parameters to achieve a desired position and orientation of the end-effector. |
| Primary Use | Simulating and predicting the robotic arm or manipulator position from known joint configurations. | Controlling the robotic arm to reach a specific point or pose. |
| Mathematical Complexity | Relatively straightforward, involves applying transformation matrices sequentially. | More complex, often requires solving nonlinear equations, may have multiple or no solutions. |
| Computation | Direct computation using kinematic equations. | Inverse problem solving, often using iterative numerical methods or optimization techniques. |
| Output | End-effector position and orientation in Cartesian space. | Joint angles or displacements. |
| Applications | Robot simulation, animation, and path verification. | Robot motion planning, control, and trajectory tracking. |
| Challenges | Less challenging; mainly involves matrix multiplications. | Potential for multiple valid and invalid solutions; requires handling of singularities and joint limits. |
Joint Angles
Joint angles are critical parameters in engineering disciplines such as biomechanics, robotics, and prosthetics, defining the relative orientation between adjacent segments connected by a joint. Precise measurement and control of joint angles optimize the design and functionality of mechanical limbs, exoskeletons, and robotic arms. Advanced sensors like goniometers and inertial measurement units (IMUs) enable real-time tracking of joint angles for dynamic analysis and adaptive control. Accurate joint angle data enhances human-machine interaction, injury prevention, and ergonomic improvements in engineered systems.
End-Effector Position
End-effector position refers to the precise spatial location of the tool or device attached to the end of a robotic arm or manipulator. It is typically expressed in Cartesian coordinates (x, y, z) within a given reference frame, enabling accurate control and interaction with the environment. Accurate determination of the end-effector position is crucial for tasks including assembly, welding, and surgical robotics, where precision within millimeter or sub-millimeter ranges is required. Advanced kinematic models and sensors such as encoders and vision systems help optimize the positioning accuracy in robotic engineering applications.
Mathematical Modeling
Mathematical modeling in engineering involves the creation of abstract representations of physical systems using mathematical expressions and algorithms to analyze and predict behavior. Engineers employ differential equations, linear algebra, and statistical models to simulate processes such as fluid dynamics, structural mechanics, and thermal systems. These models enable optimization of design parameters, improving efficiency, safety, and cost-effectiveness in projects across civil, mechanical, electrical, and aerospace engineering disciplines. Advanced computational tools like MATLAB and ANSYS facilitate the implementation and validation of mathematical models for real-world engineering applications.
Motion Planning
Motion planning in engineering involves computing feasible trajectories for robots and autonomous systems to move efficiently within their environments. Techniques such as probabilistic roadmaps (PRM) and rapidly-exploring random trees (RRT) optimize pathfinding in complex, high-dimensional spaces. Applications span robotics, aerospace, and automotive industries, where precise navigation improves safety and performance. Advances in machine learning enhance adaptive motion planning under uncertainty, supporting real-time decision-making.
Robotics Applications
Industrial robotics systems have revolutionized manufacturing by improving precision and efficiency in assembly lines. Medical robotics enable minimally invasive surgeries, enhancing patient outcomes and reducing recovery times. Service robots assist in logistics, agriculture, and hazardous environments, increasing operational safety and productivity. Advances in machine learning and sensor integration continue to expand the scope of robotics applications across various engineering disciplines.
Source and External Links
Forward and Inverse Kinematics: Explained - Iris Dynamics - Forward kinematics calculates the position and orientation of an end effector based on known joint variables, while inverse kinematics determines the joint variables needed to achieve a desired position and orientation of the end effector, often using a Jacobian matrix for computation.
Inverse vs Forward Kinematics: Everything You Need to Know - Forward kinematics is typically used for natural arc-like movements in animation by calculating the position from joint angles, whereas inverse kinematics is used when the end position is known and joint rotations must be computed, with many applications combining both for best results.
Difference Between Forward Kinematics and Inverse Kinematics - Forward kinematics answers "Where is the end effector given joint angles?" while inverse kinematics answers "What joint angles are needed for the end effector to reach a desired position?" making inverse kinematics essentially the reverse problem of forward kinematics.
FAQs
What is kinematics in robotics?
Kinematics in robotics is the study of motion of robot parts without considering forces, focusing on the positions, velocities, and accelerations of joints and end-effectors.
What are forward kinematics and inverse kinematics?
Forward kinematics calculates the end-effector position from given joint parameters, while inverse kinematics determines the joint parameters needed to achieve a desired end-effector position.
How do forward kinematics work?
Forward kinematics calculates the position and orientation of a robot's end-effector by applying joint parameters through a series of transformation matrices based on the robot's kinematic chain.
How do inverse kinematics work?
Inverse kinematics calculates joint angles needed for a robotic arm or character to reach a specific end-effector position by solving equations that relate joint parameters to the desired spatial coordinates.
What are the applications of forward kinematics?
Forward kinematics is applied in robotic arm control, animation and motion capture, computer graphics, virtual reality, biomechanical modeling, and automated manufacturing systems.
What are the challenges of inverse kinematics?
Inverse kinematics challenges include solving multiple valid solutions, handling joint limits and constraints, ensuring computational efficiency for real-time applications, managing singularities and discontinuities, and addressing the complexity of redundant degrees of freedom in robotic systems and character animation.
Why are both kinematics important in robotics?
Both forward and inverse kinematics are important in robotics because forward kinematics calculates the end-effector position from joint parameters, enabling robot movement prediction, while inverse kinematics determines joint parameters required for a desired end-effector position, essential for precise motion control and task execution.
 calledges.com
calledges.com