Hamming Code and Cyclic Redundancy Check (CRC) are essential error detection and correction methods used in digital communications and data storage. Hamming Code excels in error correction by identifying and fixing single-bit errors through parity bits, while CRC specializes in detecting burst errors using polynomial division and checksum verification. Explore the distinctions and applications of Hamming Code versus Cyclic Redundancy Check to enhance data integrity strategies.
Main Difference
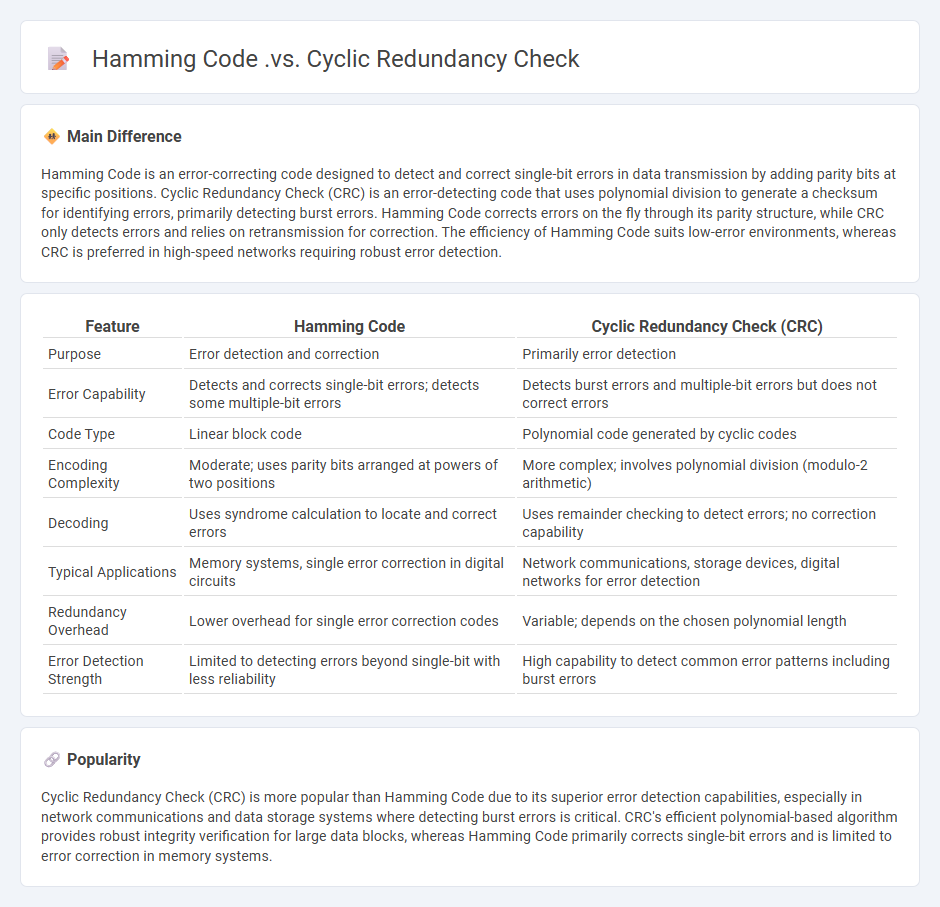
Hamming Code is an error-correcting code designed to detect and correct single-bit errors in data transmission by adding parity bits at specific positions. Cyclic Redundancy Check (CRC) is an error-detecting code that uses polynomial division to generate a checksum for identifying errors, primarily detecting burst errors. Hamming Code corrects errors on the fly through its parity structure, while CRC only detects errors and relies on retransmission for correction. The efficiency of Hamming Code suits low-error environments, whereas CRC is preferred in high-speed networks requiring robust error detection.
Connection
Hamming Code and Cyclic Redundancy Check (CRC) are both error-detection and error-correction techniques used in digital communication and data storage. Hamming Code focuses on single-bit error correction and double-bit error detection through parity bits, while CRC relies on polynomial division to detect burst errors with high accuracy. Both methods use structured redundancy to maintain data integrity but differ in complexity, with Hamming Code suitable for low-error environments and CRC preferred for detecting more complex error patterns.
Comparison Table
| Feature | Hamming Code | Cyclic Redundancy Check (CRC) |
|---|---|---|
| Purpose | Error detection and correction | Primarily error detection |
| Error Capability | Detects and corrects single-bit errors; detects some multiple-bit errors | Detects burst errors and multiple-bit errors but does not correct errors |
| Code Type | Linear block code | Polynomial code generated by cyclic codes |
| Encoding Complexity | Moderate; uses parity bits arranged at powers of two positions | More complex; involves polynomial division (modulo-2 arithmetic) |
| Decoding | Uses syndrome calculation to locate and correct errors | Uses remainder checking to detect errors; no correction capability |
| Typical Applications | Memory systems, single error correction in digital circuits | Network communications, storage devices, digital networks for error detection |
| Redundancy Overhead | Lower overhead for single error correction codes | Variable; depends on the chosen polynomial length |
| Error Detection Strength | Limited to detecting errors beyond single-bit with less reliability | High capability to detect common error patterns including burst errors |
Error Detection
Error detection in engineering involves identifying faults or anomalies in systems, components, or processes to ensure safety, reliability, and performance. Techniques such as parity checks, cyclic redundancy checks (CRC), and built-in self-tests (BIST) are frequently used in hardware engineering to detect errors in data transmission and storage. In software engineering, static code analysis and runtime monitoring help uncover logical errors and vulnerabilities. Accurate error detection minimizes downtime and maintenance costs across various fields including automotive, aerospace, and manufacturing industries.
Error Correction
Error correction in engineering involves techniques to detect and fix faults in systems, ensuring reliability and accuracy in data transmission and processing. Common methods include error detection codes like parity bits and error correction codes such as Reed-Solomon and Hamming codes, which are widely implemented in communication systems and digital storage. Modern engineering applications leverage forward error correction (FEC) to enhance performance in wireless networks, satellite communications, and data centers. Advanced algorithms combined with hardware implementations enable real-time error correction critical for autonomous vehicles and aerospace technology.
Parity Bits
Parity bits are crucial error-detection tools in digital communication and data storage systems, ensuring data integrity by indicating whether the number of set bits is odd or even. Commonly implemented in memory modules, parity bits enable detection of single-bit errors during data transmission or retrieval. Systems using even parity assign the parity bit to maintain an even count of ones, while odd parity systems maintain an odd count. Parity checking plays a foundational role in engineering disciplines such as computer architecture and telecommunications.
Redundancy Checks
Redundancy checks in engineering are critical for ensuring system reliability and fault tolerance by providing backup components or pathways that activate during primary system failures. Techniques such as parity checks, cyclic redundancy checks (CRC), and modular redundancy are employed to detect and correct errors in data communication and hardware operations. Industries like aerospace, automotive, and telecommunications extensively implement redundancy to meet safety standards like DO-178C and ISO 26262. Effective redundancy reduces downtime and enhances system robustness, directly contributing to operational efficiency and safety compliance.
Syndrome Calculation
Syndrome calculation in engineering primarily refers to error detection and correction in coding theory, especially within digital communications and data storage systems. This process involves computing the syndrome vector by multiplying the received message by the transpose of the parity-check matrix, which helps identify error patterns without knowing the original codeword. Commonly applied in cyclic codes and linear block codes, syndrome calculation enables efficient error localization and correction, enhancing system reliability and data integrity. Techniques like the Berlekamp-Massey algorithm utilize syndrome values to reconstruct error sequences in practical engineering applications.
Source and External Links
Solved: Difference between CRC and Hamming Code - This article explains the difference between Hamming codes, which can detect and correct errors, and CRC, which only detects errors by using polynomial division.
Is the Cyclic Redundancy Check Better Than Hamming Code? - This explanation highlights that CRC is more efficient for detecting errors over large data blocks, while Hamming codes are effective for correcting errors in smaller data sets like individual bytes.
Cyclic Redundancy Check - This Wikipedia page provides details on CRC, an error-detecting code used in networks and storage devices, which is efficient due to its simplicity and effectiveness in detecting common transmission errors.
FAQs
What is Hamming Code?
Hamming Code is an error-detecting and error-correcting binary code that uses parity bits to identify and correct single-bit errors in data transmission.
What is Cyclic Redundancy Check?
Cyclic Redundancy Check (CRC) is an error-detecting code used to detect accidental changes in raw data during transmission or storage by generating a fixed-size checksum based on polynomial division of the data bits.
How does Hamming Code detect and correct errors?
Hamming Code detects errors by calculating parity bits based on specific positions in the binary data; when a parity check fails, it identifies the exact bit position with an error using the binary sum of parity checks, then corrects the single-bit error by flipping that bit.
How does Cyclic Redundancy Check detect errors?
Cyclic Redundancy Check (CRC) detects errors by dividing the transmitted data polynomial by a predetermined generator polynomial and comparing the remainder with the sent CRC value; any discrepancy indicates data corruption.
What are the main differences between Hamming Code and CRC?
Hamming Code detects and corrects single-bit errors using parity bits, applied mainly in memory error correction, while CRC detects multiple-bit errors using polynomial division for error checking in data transmission and storage.
Where is Hamming Code commonly used?
Hamming Code is commonly used in computer memory error detection and correction, telecommunications, and data storage systems.
Where is Cyclic Redundancy Check commonly used?
Cyclic Redundancy Check (CRC) is commonly used in network communications, storage devices, and data transmission protocols to detect errors.
 calledges.com
calledges.com