Nonlinear control deals with systems whose behavior cannot be accurately described by linear equations, making it essential for handling real-world complexities such as saturation, dead zones, or hysteresis. Linear control simplifies system dynamics into linear approximations, facilitating easier analysis and design but often at the cost of reduced accuracy in non-ideal conditions. Explore the key differences and applications of nonlinear versus linear control to optimize system performance in diverse engineering fields.
Main Difference
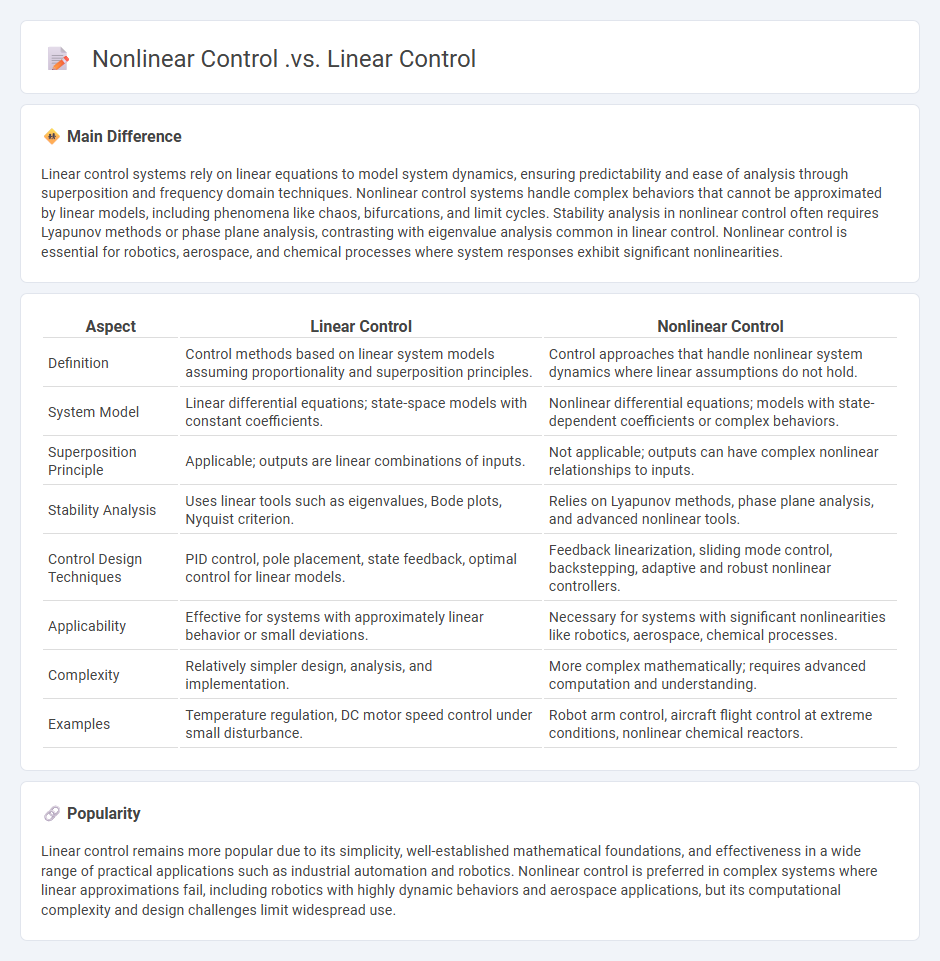
Linear control systems rely on linear equations to model system dynamics, ensuring predictability and ease of analysis through superposition and frequency domain techniques. Nonlinear control systems handle complex behaviors that cannot be approximated by linear models, including phenomena like chaos, bifurcations, and limit cycles. Stability analysis in nonlinear control often requires Lyapunov methods or phase plane analysis, contrasting with eigenvalue analysis common in linear control. Nonlinear control is essential for robotics, aerospace, and chemical processes where system responses exhibit significant nonlinearities.
Connection
Nonlinear control extends linear control principles by addressing systems with nonlinear dynamics that cannot be adequately handled by linear models alone. Techniques such as feedback linearization transform nonlinear systems into linear equivalents, enabling the use of linear control methods for design and analysis. This connection allows engineers to apply well-established linear control tools to complex nonlinear systems, improving stability and performance in various applications.
Comparison Table
| Aspect | Linear Control | Nonlinear Control |
|---|---|---|
| Definition | Control methods based on linear system models assuming proportionality and superposition principles. | Control approaches that handle nonlinear system dynamics where linear assumptions do not hold. |
| System Model | Linear differential equations; state-space models with constant coefficients. | Nonlinear differential equations; models with state-dependent coefficients or complex behaviors. |
| Superposition Principle | Applicable; outputs are linear combinations of inputs. | Not applicable; outputs can have complex nonlinear relationships to inputs. |
| Stability Analysis | Uses linear tools such as eigenvalues, Bode plots, Nyquist criterion. | Relies on Lyapunov methods, phase plane analysis, and advanced nonlinear tools. |
| Control Design Techniques | PID control, pole placement, state feedback, optimal control for linear models. | Feedback linearization, sliding mode control, backstepping, adaptive and robust nonlinear controllers. |
| Applicability | Effective for systems with approximately linear behavior or small deviations. | Necessary for systems with significant nonlinearities like robotics, aerospace, chemical processes. |
| Complexity | Relatively simpler design, analysis, and implementation. | More complex mathematically; requires advanced computation and understanding. |
| Examples | Temperature regulation, DC motor speed control under small disturbance. | Robot arm control, aircraft flight control at extreme conditions, nonlinear chemical reactors. |
System Linearity
System linearity in engineering refers to the property of a system where the output response is directly proportional to the input, adhering to the principles of superposition and homogeneity. Linear systems can be modeled using linear differential equations, enabling straightforward analysis and design in control systems, signal processing, and circuit theory. Practical examples include linear time-invariant (LTI) systems, which maintain consistent behavior over time and are crucial in stability and frequency response analysis. Understanding system linearity allows engineers to predict system behavior accurately and apply linear control techniques for efficient performance optimization.
Stability Analysis
Stability analysis in engineering assesses the ability of structures, systems, or materials to maintain equilibrium under various loads and disturbances. Techniques such as linear stability analysis, eigenvalue methods, and Lyapunov stability are applied to predict potential failure modes and ensure safety in mechanical, civil, and aerospace engineering. Key applications include evaluating the buckling of columns, vibration control in mechanical systems, and stability of control systems in robotics. Accurate stability analysis helps optimize design parameters, reducing the risk of catastrophic failure and improving overall system performance.
Superposition Principle
The Superposition Principle in engineering states that the response in any linear system caused by multiple independent sources is the sum of the responses caused by each source acting alone. This principle is widely used in structural analysis, electrical circuit design, and mechanical systems to simplify complex problems. For instance, in electrical engineering, it enables the calculation of currents and voltages in circuits with multiple voltage sources by considering each source separately. Applying the Superposition Principle ensures accurate modeling and efficient design of systems governed by linear equations.
Feedback Mechanisms
Feedback mechanisms in engineering regulate system behavior by continuously monitoring output and adjusting inputs to maintain desired performance levels. These processes are integral to control systems in disciplines such as electrical, mechanical, and chemical engineering, ensuring stability and minimizing errors. Common examples include proportional-integral-derivative (PID) controllers, which optimize automation in manufacturing and robotics. Advanced feedback loops also enhance adaptive systems by responding dynamically to environmental changes and operational disturbances.
Real-world Applications
Engineering drives innovation across numerous real-world applications, including aerospace design, civil infrastructure, and renewable energy systems. Advanced materials engineering enhances the durability and performance of automotive components, while environmental engineering addresses water purification and pollution control. Structural engineering ensures the safety and resilience of skyscrapers and bridges in seismic zones. Automation and robotics engineering improve manufacturing efficiency and precision across industries.
Source and External Links
Linear and Non-Linear Control System - GeeksforGeeks - Linear control systems follow predictable, consistent input-output relationships and obey the principle of superposition, while nonlinear control systems exhibit complex, unpredictable behaviors that deviate from linearity especially beyond certain operating thresholds.
Nonlinear control - Wikipedia - Nonlinear control systems do not follow linear superposition, may have multiple equilibrium points, can exhibit limit cycles or chaotic behavior, and require specialized analysis and design techniques such as Lyapunov methods, feedback linearization, and sliding mode control.
1.2 Differences between linear and nonlinear systems - Fiveable - Nonlinear systems are more complex than linear systems because they do not obey superposition and can have multiple equilibrium points, making nonlinear control more challenging but allowing for rich dynamic behaviors like chaos and limit cycles.
FAQs
What is control in engineering?
Control in engineering is the process of designing systems that regulate the behavior of devices or processes to achieve desired outputs by manipulating inputs based on feedback.
What is the main difference between nonlinear and linear control?
Nonlinear control handles systems with nonlinear dynamics where outputs are not proportional to inputs, while linear control deals with systems modeled by linear equations exhibiting proportional input-output relationships.
When is nonlinear control necessary?
Nonlinear control is necessary when system dynamics exhibit significant nonlinear behavior that cannot be accurately modeled or controlled using linear approximations, such as in robotic manipulators, aerospace vehicles, chemical reactors, and biological systems operating under varying conditions.
What are typical examples of nonlinear systems?
Typical examples of nonlinear systems include weather and climate models, population dynamics in ecology, electrical circuits with diodes or transistors, chaotic pendulums, chemical reaction kinetics, and neural networks.
How does linear control simplify analysis?
Linear control simplifies analysis by enabling the use of superposition, linear differential equations, and well-established mathematical tools like Laplace transforms, which facilitate straightforward system modeling, stability assessment, and response prediction.
What are the challenges of nonlinear control?
Nonlinear control challenges include system modeling complexity, stability analysis difficulty, controller design intricacies, sensitivity to parameter variations, and computational burden for real-time implementation.
Why choose linear control over nonlinear control?
Choose linear control for simpler design, easier analysis, well-established stability criteria, and efficient implementation in systems operating near equilibrium points.
 calledges.com
calledges.com