Monte Carlo Simulation relies on random sampling to explore the statistical properties of systems, providing insights into equilibrium states and thermodynamic quantities. Molecular Dynamics Simulation, on the other hand, computes the time-dependent behavior of atoms and molecules by solving classical equations of motion, enabling detailed analysis of dynamic processes and structural evolution. Discover the key differences and applications to select the ideal method for your research needs.
Main Difference
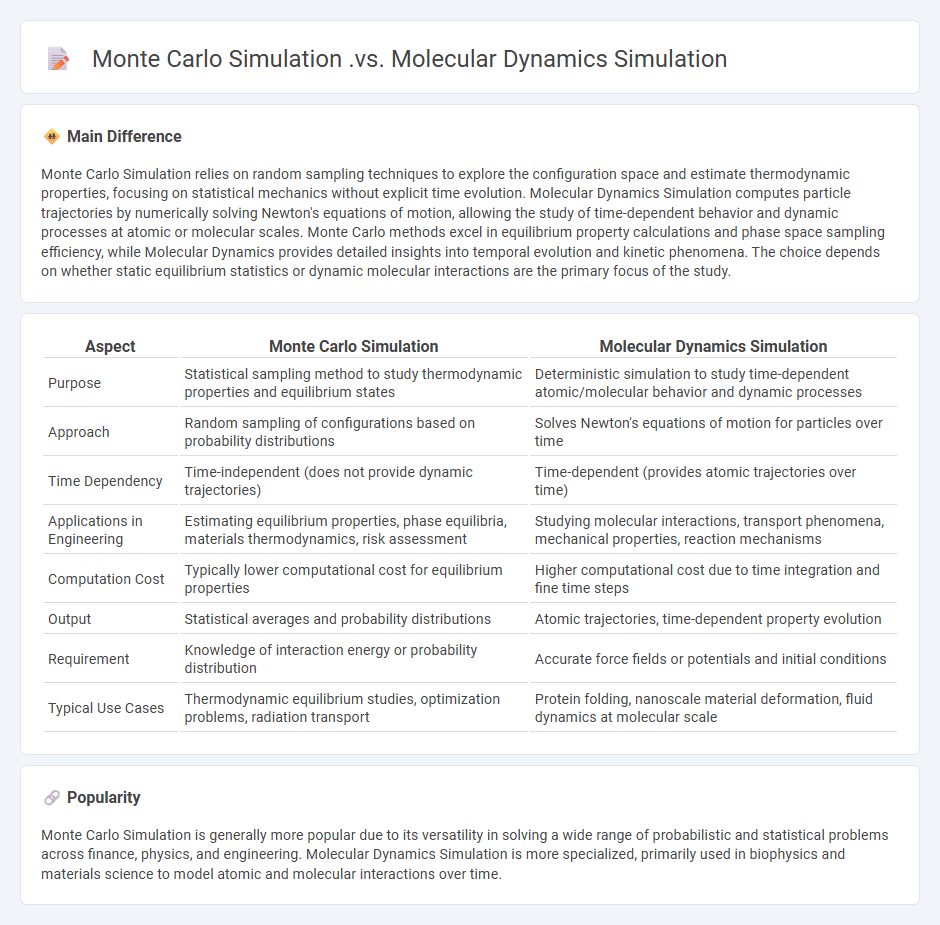
Monte Carlo Simulation relies on random sampling techniques to explore the configuration space and estimate thermodynamic properties, focusing on statistical mechanics without explicit time evolution. Molecular Dynamics Simulation computes particle trajectories by numerically solving Newton's equations of motion, allowing the study of time-dependent behavior and dynamic processes at atomic or molecular scales. Monte Carlo methods excel in equilibrium property calculations and phase space sampling efficiency, while Molecular Dynamics provides detailed insights into temporal evolution and kinetic phenomena. The choice depends on whether static equilibrium statistics or dynamic molecular interactions are the primary focus of the study.
Connection
Monte Carlo Simulation and Molecular Dynamics Simulation both model molecular systems but differ in approach: Monte Carlo uses stochastic sampling to explore configurational space, while Molecular Dynamics solves Newton's equations of motion to generate time-dependent trajectories. They complement each other in studying thermodynamic properties, as Monte Carlo efficiently samples equilibrium states and Molecular Dynamics provides dynamic behavior insights. Combining both methods enhances accuracy in predicting molecular interactions and material properties in computational chemistry and physics.
Comparison Table
| Aspect | Monte Carlo Simulation | Molecular Dynamics Simulation |
|---|---|---|
| Purpose | Statistical sampling method to study thermodynamic properties and equilibrium states | Deterministic simulation to study time-dependent atomic/molecular behavior and dynamic processes |
| Approach | Random sampling of configurations based on probability distributions | Solves Newton's equations of motion for particles over time |
| Time Dependency | Time-independent (does not provide dynamic trajectories) | Time-dependent (provides atomic trajectories over time) |
| Applications in Engineering | Estimating equilibrium properties, phase equilibria, materials thermodynamics, risk assessment | Studying molecular interactions, transport phenomena, mechanical properties, reaction mechanisms |
| Computation Cost | Typically lower computational cost for equilibrium properties | Higher computational cost due to time integration and fine time steps |
| Output | Statistical averages and probability distributions | Atomic trajectories, time-dependent property evolution |
| Requirement | Knowledge of interaction energy or probability distribution | Accurate force fields or potentials and initial conditions |
| Typical Use Cases | Thermodynamic equilibrium studies, optimization problems, radiation transport | Protein folding, nanoscale material deformation, fluid dynamics at molecular scale |
Probability-based Sampling vs Deterministic Trajectories
Probability-based sampling in engineering leverages randomization to model complex systems, enabling robust uncertainty quantification and improved predictive accuracy. Deterministic trajectories, however, follow predefined paths calculated from known parameters, offering precise outcomes when system behaviors are predictable. Monte Carlo simulations exemplify probability-based techniques by sampling numerous scenarios to approximate system responses, whereas deterministic methods dominate in control systems and path planning with fixed inputs. Integrating both approaches enhances reliability in engineering designs, particularly in aerospace and robotics.
Time Evolution vs Equilibrium Properties
Time evolution in engineering systems analyzes dynamic changes and transient behaviors under varying conditions, using differential equations and computational simulations to predict system responses over time. Equilibrium properties focus on steady-state conditions where all forces and reactions balance, allowing simplified analysis through static models and thermodynamic principles. Understanding time evolution enables engineers to design systems that withstand fluctuations and adapt to real-world disturbances, while equilibrium analysis ensures structural integrity and efficiency in stable operating conditions. Combining both approaches optimizes performance in mechanical, chemical, and electrical engineering applications.
Random Walk Algorithms vs Newtonian Mechanics
Random walk algorithms model stochastic processes by simulating paths consisting of successive random steps, crucial for optimizing complex engineering systems under uncertainty. Newtonian mechanics governs the deterministic motion of physical bodies through differential equations based on mass, force, and acceleration, enabling precise prediction of dynamic system behavior. In engineering, random walk techniques are extensively employed in probabilistic analysis, such as heat transfer simulations and material fatigue modeling, where random fluctuations affect system performance. Newtonian mechanics underpins classical mechanics-based design, including structural analysis, fluid dynamics, and control systems, ensuring engineered solutions adhere to fundamental physical laws.
Statistical Thermodynamics vs Dynamic Behavior
Statistical thermodynamics applies probabilistic methods to predict the macroscopic properties of engineering systems based on molecular-level interactions, enabling precise modeling of thermodynamic equilibrium states. Dynamic behavior in engineering focuses on time-dependent system responses, analyzing changes in state variables such as temperature, pressure, and volume under transient conditions. Combining statistical thermodynamics with dynamic analysis facilitates enhanced design of thermal systems, optimizing performance and stability in applications like heat exchangers, combustion engines, and refrigeration cycles. Real-time data integration from sensors further refines predictive models, supporting adaptive control strategies in complex engineering processes.
Material Design Applications vs Process Simulation
Material design applications in engineering focus on developing materials with tailored properties for specific uses, enhancing structural performance and durability. Process simulation involves creating digital models to analyze and optimize manufacturing processes, reducing costs and improving efficiency. Integrating material design with process simulation allows engineers to predict material behavior under various conditions, leading to innovative solutions and faster product development. This synergy is critical in industries like aerospace, automotive, and electronics where precision and reliability are paramount.
Source and External Links
Monte Carlo molecular modeling - Monte Carlo simulation relies on equilibrium statistical mechanics generating states based on Boltzmann distribution without simulating system dynamics, making it suitable for static quantity studies, whereas molecular dynamics simulates actual time evolution of systems through Newtonian equations of motion.
Molecular Dynamics, Monte Carlo Simulations, and ... - Monte Carlo simulations generate ensembles of configurations by random perturbations without time evolution, focusing on thermodynamic sampling, while molecular dynamics simulates realistic time-dependent trajectories of molecular systems.
Molecular Dynamics and Monte Carlo - Molecular dynamics is a deterministic method integrating Newton's equations to simulate particle motions over time, while Monte Carlo is stochastic, focusing on sampling system states based on potential energy and usually constrained to canonical ensembles without time information.
FAQs
What is a simulation in computational science?
A simulation in computational science is a computer-based model that replicates real-world processes or systems to analyze behaviors and predict outcomes.
What is Monte Carlo simulation?
Monte Carlo simulation is a computational technique that uses random sampling and statistical modeling to estimate the probability distribution of complex systems and uncertain outcomes.
What is Molecular Dynamics simulation?
Molecular Dynamics simulation is a computational method that models the physical movements of atoms and molecules over time using Newtonian mechanics to study the structure, dynamics, and thermodynamic properties of complex molecular systems.
How do Monte Carlo and Molecular Dynamics simulations differ?
Monte Carlo simulations use random sampling to explore configurational space based on probability distributions, while Molecular Dynamics simulations compute time-dependent particle trajectories by numerically integrating Newton's equations of motion.
What are the inputs required for Monte Carlo simulation?
Inputs required for Monte Carlo simulation include defined probability distributions for uncertain variables, initial conditions, a mathematical or computational model representing the system, the number of simulation iterations, and random number generators.
What are the inputs required for Molecular Dynamics simulation?
The inputs required for Molecular Dynamics simulation are the initial coordinates of atoms, the initial velocities, the force field parameters (including potential energy functions and parameters), system temperature, pressure conditions, and simulation timestep.
In which scenarios is Monte Carlo simulation more suitable than Molecular Dynamics simulation?
Monte Carlo simulation is more suitable than Molecular Dynamics simulation for equilibrium thermodynamic property estimation, systems with complex potential energy surfaces, and scenarios requiring efficient sampling of configurational space without detailed time evolution.
 calledges.com
calledges.com