PD controllers provide proportional and derivative control actions to improve system stability and response speed, making them ideal for applications requiring precise error correction and quick reaction. PI controllers combine proportional and integral actions to eliminate steady-state error and enhance system accuracy, commonly used in processes with slow dynamics. Explore the differences between PD and PI controllers to optimize your control system design.
Main Difference
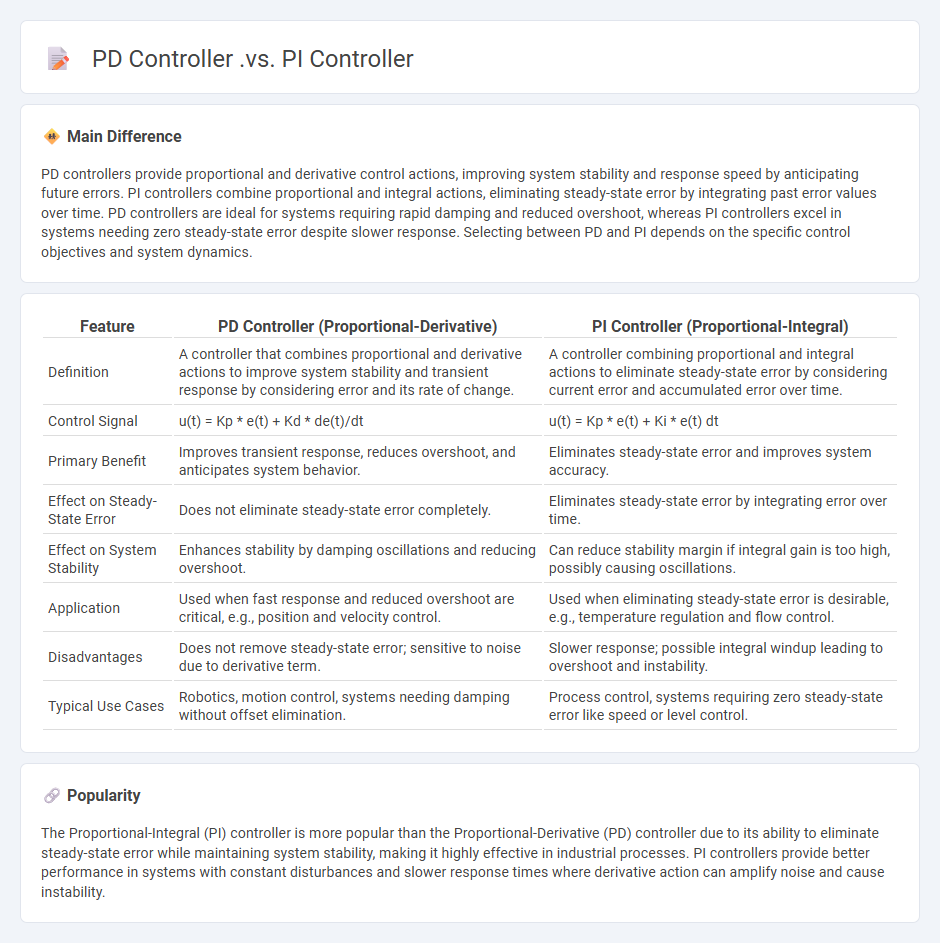
PD controllers provide proportional and derivative control actions, improving system stability and response speed by anticipating future errors. PI controllers combine proportional and integral actions, eliminating steady-state error by integrating past error values over time. PD controllers are ideal for systems requiring rapid damping and reduced overshoot, whereas PI controllers excel in systems needing zero steady-state error despite slower response. Selecting between PD and PI depends on the specific control objectives and system dynamics.
Connection
PD controllers enhance system stability by adjusting proportional and derivative actions, while PI controllers reduce steady-state error using proportional and integral components. Combining these controllers in a control system leverages the derivative action of the PD controller to improve transient response and the integral action of the PI controller to eliminate steady-state error. This complementary integration results in a robust control strategy optimizing both speed and accuracy in system performance.
Comparison Table
| Feature | PD Controller (Proportional-Derivative) | PI Controller (Proportional-Integral) |
|---|---|---|
| Definition | A controller that combines proportional and derivative actions to improve system stability and transient response by considering error and its rate of change. | A controller combining proportional and integral actions to eliminate steady-state error by considering current error and accumulated error over time. |
| Control Signal | u(t) = Kp * e(t) + Kd * de(t)/dt | u(t) = Kp * e(t) + Ki * e(t) dt |
| Primary Benefit | Improves transient response, reduces overshoot, and anticipates system behavior. | Eliminates steady-state error and improves system accuracy. |
| Effect on Steady-State Error | Does not eliminate steady-state error completely. | Eliminates steady-state error by integrating error over time. |
| Effect on System Stability | Enhances stability by damping oscillations and reducing overshoot. | Can reduce stability margin if integral gain is too high, possibly causing oscillations. |
| Application | Used when fast response and reduced overshoot are critical, e.g., position and velocity control. | Used when eliminating steady-state error is desirable, e.g., temperature regulation and flow control. |
| Disadvantages | Does not remove steady-state error; sensitive to noise due to derivative term. | Slower response; possible integral windup leading to overshoot and instability. |
| Typical Use Cases | Robotics, motion control, systems needing damping without offset elimination. | Process control, systems requiring zero steady-state error like speed or level control. |
Proportional-Derivative (PD) Controller
A Proportional-Derivative (PD) controller is a fundamental feedback control mechanism widely used in engineering for precise system regulation. It combines proportional control, which adjusts output proportionally to the current error, with derivative control, which predicts future errors based on the rate of change. This hybrid approach enhances system stability and response speed, particularly in mechanical and electrical engineering applications such as robotics and motor control. The PD controller is essential for minimizing overshoot and improving transient response in dynamic systems.
Proportional-Integral (PI) Controller
Proportional-Integral (PI) controllers are widely used in engineering to regulate process variables by minimizing the error between a desired setpoint and the actual output. The proportional component produces an output proportional to the current error, while the integral component accounts for the accumulation of past errors, enhancing system stability and ensuring zero steady-state error. PI controllers are fundamental in industrial automation, including temperature control, motor speed regulation, and flow systems, due to their simplicity and effective disturbance rejection. Their tuning typically involves methods such as Ziegler-Nichols and Cohen-Coon to optimize performance for specific applications.
Steady-State Error
Steady-state error in engineering measures the difference between an input command and the actual output of a control system as time approaches infinity. It quantifies the system's accuracy in reaching and maintaining a desired setpoint under constant input conditions. Commonly analyzed in feedback control systems, steady-state error depends on system type, controller design, and input signal characteristics such as step, ramp, or parabolic inputs. Techniques like proportional-integral-derivative (PID) control or feedforward compensation are employed to minimize steady-state error and improve system performance.
System Stability and Response Time
System stability ensures continuous, reliable performance under varying conditions, minimizing failures and downtime in engineering applications. Response time measures the speed at which a system reacts to inputs, directly impacting user experience and operational efficiency. Advanced control algorithms and real-time monitoring technologies enhance both stability and response time by swiftly detecting and correcting anomalies. Engineering systems such as automotive control units and industrial automation rely heavily on optimized stability and rapid response to maintain safety and productivity.
Industrial Process Control Applications
Industrial process control applications optimize manufacturing efficiency by integrating advanced sensors, programmable logic controllers (PLCs), and real-time data analytics. These systems enable precise regulation of temperature, pressure, flow rate, and chemical composition in industries such as oil and gas, pharmaceuticals, and food processing. Implementing distributed control systems (DCS) enhances scalability and fault tolerance, reducing downtime and operational costs. Continuous feedback loops improve product quality while ensuring compliance with industry standards and safety regulations.
Source and External Links
PD vs PI vs PID Controllers: A Detailed Comparison - A PD controller improves transient response, increases damping, and reduces peak overshoot but amplifies high-frequency noise; a PI controller improves steady-state response, eliminates steady-state error, and reduces noise but may reduce bandwidth and slow response.
Comparison of P PI PD and PID Controllers - PD controllers improve settling time and reduce overshoot but cannot eliminate steady-state error, unlike PI controllers which eliminate steady-state error but have slower response and add poles that may affect stability.
3.3: PI, PD, and PID Controllers - PI controllers combine proportional and integral actions to eliminate steady-state error and improve tracking, while PD controllers combine proportional and derivative actions to speed response and increase stability but do not remove steady-state error.
FAQs
What is a PD controller?
A PD controller is a proportional-derivative control system that adjusts output based on the current error and its rate of change to improve stability and response time.
What is a PI controller?
A PI controller is a proportional-integral control system used in automation to maintain a desired setpoint by adjusting control inputs based on the error and the accumulation of past errors.
How does a PD controller work?
A PD controller operates by combining proportional control, which adjusts output based on the current error magnitude, with derivative control, which predicts future error trends by evaluating the rate of error change, thereby improving system stability and response time.
How does a PI controller work?
A PI controller works by continuously calculating the error between a desired setpoint and a measured process variable, then adjusting the control input using proportional and integral terms to minimize this error over time.
What are the key differences between PD and PI controllers?
PD controllers use proportional and derivative terms to improve transient response and reduce overshoot, while PI controllers combine proportional and integral terms to eliminate steady-state error and improve accuracy.
When should you use a PD controller instead of a PI controller?
Use a PD controller when the system requires improved transient response and reduced overshoot without steady-state error compensation, typically in systems where eliminating steady-state error is not critical.
What are the advantages and disadvantages of PD and PI controllers?
PD controllers offer improved system stability and faster response by reducing overshoot and damping oscillations but lack steady-state error elimination. PI controllers eliminate steady-state errors and improve accuracy but may cause slower response and increased overshoot due to lack of derivative action.
 calledges.com
calledges.com