The Single Index Model simplifies portfolio risk by attributing asset returns to a single market factor, often represented by a broad market index, enabling efficient beta estimation. In contrast, the Multi-Factor Model expands risk analysis by incorporating multiple systematic factors such as interest rates, industrial production, and inflation, offering a more comprehensive view of asset price behavior. Explore the differences and applications of these models to enhance your investment strategy analysis.
Main Difference
The Single Index Model explains stock returns using a single common factor, typically the market index, to capture systematic risk. The Multi-Factor Model incorporates multiple factors, such as size, value, and momentum, to better explain variations in asset returns by addressing various sources of systematic risk. Single Index Models are simpler but less precise, while Multi-Factor Models improve explanatory power by capturing complexities in market behavior. Empirical research shows Multi-Factor Models often provide superior risk-adjusted performance measures compared to Single Index Models.
Connection
The Single Index Model (SIM) is a simplified version of the Multi-Factor Model where the market index serves as the sole explanatory factor for asset returns. Multi-Factor Models extend this framework by incorporating multiple risk factors such as industry indices, macroeconomic variables, or fundamental indicators, offering a more comprehensive explanation of asset return variability. Both models rely on factor loadings to quantify an asset's sensitivity to systematic risk factors, facilitating portfolio optimization and risk management.
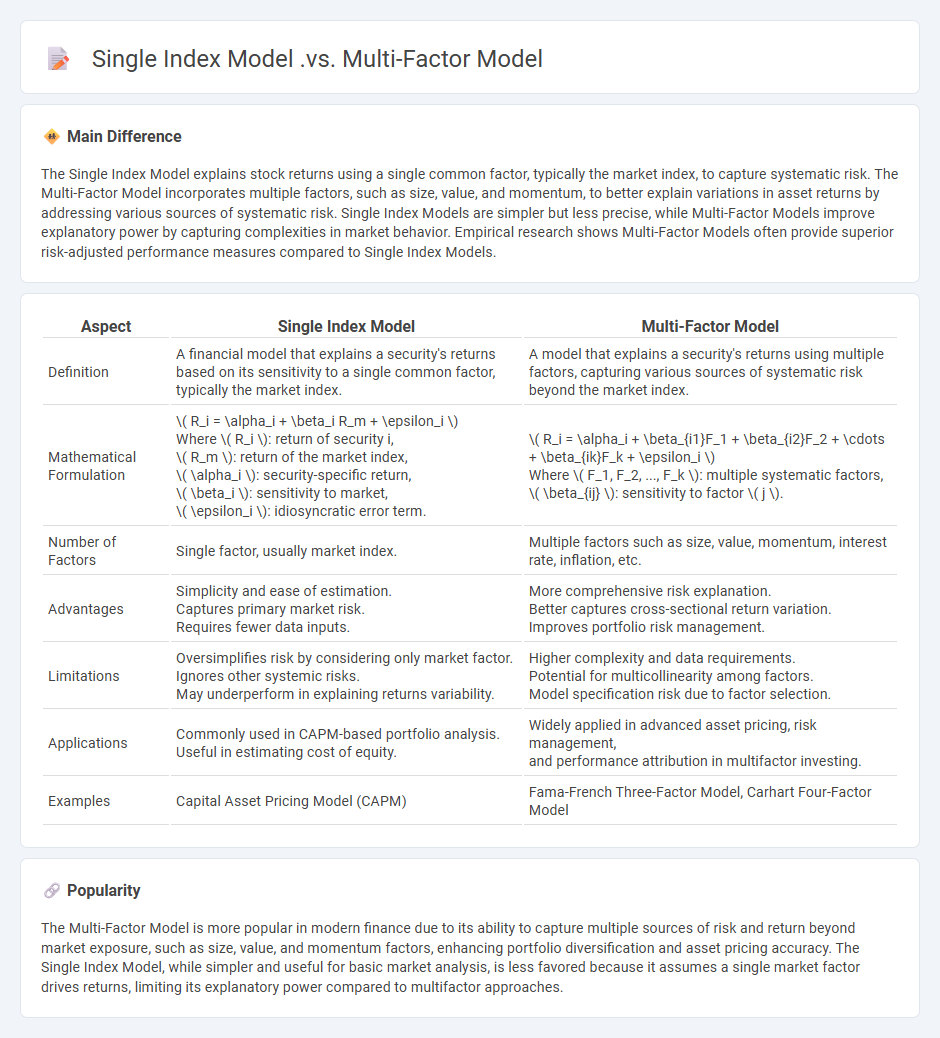
Comparison Table
| Aspect | Single Index Model | Multi-Factor Model |
|---|---|---|
| Definition | A financial model that explains a security's returns based on its sensitivity to a single common factor, typically the market index. | A model that explains a security's returns using multiple factors, capturing various sources of systematic risk beyond the market index. |
| Mathematical Formulation |
\( R_i = \alpha_i + \beta_i R_m + \epsilon_i \) Where \( R_i \): return of security i, \( R_m \): return of the market index, \( \alpha_i \): security-specific return, \( \beta_i \): sensitivity to market, \( \epsilon_i \): idiosyncratic error term. |
\( R_i = \alpha_i + \beta_{i1}F_1 + \beta_{i2}F_2 + \cdots + \beta_{ik}F_k + \epsilon_i \) Where \( F_1, F_2, ..., F_k \): multiple systematic factors, \( \beta_{ij} \): sensitivity to factor \( j \). |
| Number of Factors | Single factor, usually market index. | Multiple factors such as size, value, momentum, interest rate, inflation, etc. |
| Advantages |
Simplicity and ease of estimation. Captures primary market risk. Requires fewer data inputs. |
More comprehensive risk explanation. Better captures cross-sectional return variation. Improves portfolio risk management. |
| Limitations |
Oversimplifies risk by considering only market factor. Ignores other systemic risks. May underperform in explaining returns variability. |
Higher complexity and data requirements. Potential for multicollinearity among factors. Model specification risk due to factor selection. |
| Applications |
Commonly used in CAPM-based portfolio analysis. Useful in estimating cost of equity. |
Widely applied in advanced asset pricing, risk management, and performance attribution in multifactor investing. |
| Examples | Capital Asset Pricing Model (CAPM) | Fama-French Three-Factor Model, Carhart Four-Factor Model |
Systematic Risk
Systematic risk represents the inherent market risk that affects all securities and cannot be eliminated through diversification. Key factors influencing systematic risk include economic recessions, interest rate changes, geopolitical events, and inflation fluctuations. Measured by beta (b), stocks with a beta greater than 1 are more volatile than the overall market. Investors assess systematic risk to optimize portfolio performance and manage exposure to market-wide uncertainties.
Factor Loadings
Factor loadings in finance represent the correlations between observed variables, such as asset returns, and underlying latent factors driving market behavior. These loadings quantify the sensitivity of an asset's returns to systematic risk factors like market index returns, interest rates, or macroeconomic variables. In multifactor models such as the Fama-French three-factor model, factor loadings determine the exposure of stocks to size, value, and market risk premiums. Accurate estimation of factor loadings improves portfolio optimization and risk management by isolating sources of systematic risk.
Diversification
Diversification in finance involves spreading investments across various asset classes, sectors, and geographic regions to reduce overall portfolio risk. By allocating capital to stocks, bonds, real estate, and alternative investments, investors minimize exposure to any single asset's volatility. According to Modern Portfolio Theory, diversification enhances risk-adjusted returns by leveraging low or negative correlations between assets. Empirical data from Morningstar indicates diversified portfolios typically experience lower standard deviation and improved long-term growth compared to concentrated holdings.
Regression Analysis
Regression analysis in finance quantifies relationships between dependent financial variables and one or more independent variables, enabling accurate modeling of asset prices, risk factors, and market trends. It supports portfolio optimization by estimating expected returns and assessing systematic risk through beta coefficients in the Capital Asset Pricing Model (CAPM). Financial institutions leverage regression techniques to forecast earnings, evaluate credit risk, and detect arbitrage opportunities. Prominent regression methods include linear regression, logistic regression, and multivariate regression, tailored to complex financial datasets.
Asset Pricing
Asset pricing models explain how financial assets are valued based on risk, cash flows, and market conditions. The Capital Asset Pricing Model (CAPM) quantifies expected returns by relating an asset's systematic risk to market returns. Arbitrage Pricing Theory (APT) extends this by incorporating multiple risk factors beyond market risk. Empirical studies utilize asset pricing to assess market efficiency and guide portfolio management decisions.
Source and External Links
Index Models - NYU Stern - The Single Index Model (SIM) relates individual asset returns linearly to a single market index factor, simplifying portfolio optimization by reducing parameters but assuming all asset correlations depend on this single factor;
Return Generating Models | CFA Level 1 - AnalystPrep - The Single Index Model uses the market return as the sole factor explaining security returns, whereas multi-factor models incorporate multiple sources of systematic risk beyond the market, offering greater explanatory power;
Using Multifactor Models - CFA Institute - Multifactor models extend single-index models by including several factors correlated with asset returns, enabling more granular risk and return attribution, better portfolio construction, and enhanced risk management compared to single-factor approaches.
FAQs
What is the Single Index Model?
The Single Index Model is a financial model that explains individual stock returns using a single market index as the systematic risk factor, represented by the equation: Ri = ai + biRm + ei, where Ri is the stock return, Rm is the market return, ai is the stock's alpha, bi is the beta coefficient measuring sensitivity to market movements, and ei is the idiosyncratic error term.
What is the Multi-Factor Model?
The Multi-Factor Model is a financial model that explains asset returns by incorporating multiple risk factors, such as market risk, size, value, and momentum, to better capture the sources of systematic risk beyond the single market factor.
How do Single Index and Multi-Factor Models differ?
Single Index Models use one common factor, typically the market index, to explain asset returns, while Multi-Factor Models incorporate multiple factors such as size, value, and momentum to capture a broader range of return drivers.
What are the assumptions of the Single Index Model?
The Single Index Model assumes that asset returns are linearly related to a single common factor (market index), residuals are uncorrelated across assets with zero mean and constant variance, and market returns have a non-zero variance.
What are the advantages of using Multi-Factor Models?
Multi-Factor Models enhance risk assessment accuracy, improve portfolio diversification, identify key return drivers, and enable better performance attribution analysis.
When should you use a Single Index Model?
Use a Single Index Model when you need to estimate asset returns based on their sensitivity to a single common factor, such as the market index, to simplify portfolio risk assessment and reduce computational complexity.
When is the Multi-Factor Model preferred?
The Multi-Factor Model is preferred when analyzing asset returns influenced by multiple systematic risk factors beyond market risk, enabling more precise risk assessment and portfolio optimization.
 calledges.com
calledges.com