Currying transforms a function with multiple arguments into a sequence of functions each taking a single argument, enabling fine-grained function invocation. Partial application fixes a subset of a function's arguments, producing a new function that requires fewer parameters for subsequent calls. Explore the differences and use cases of currying and partial application to enhance functional programming skills.
Main Difference
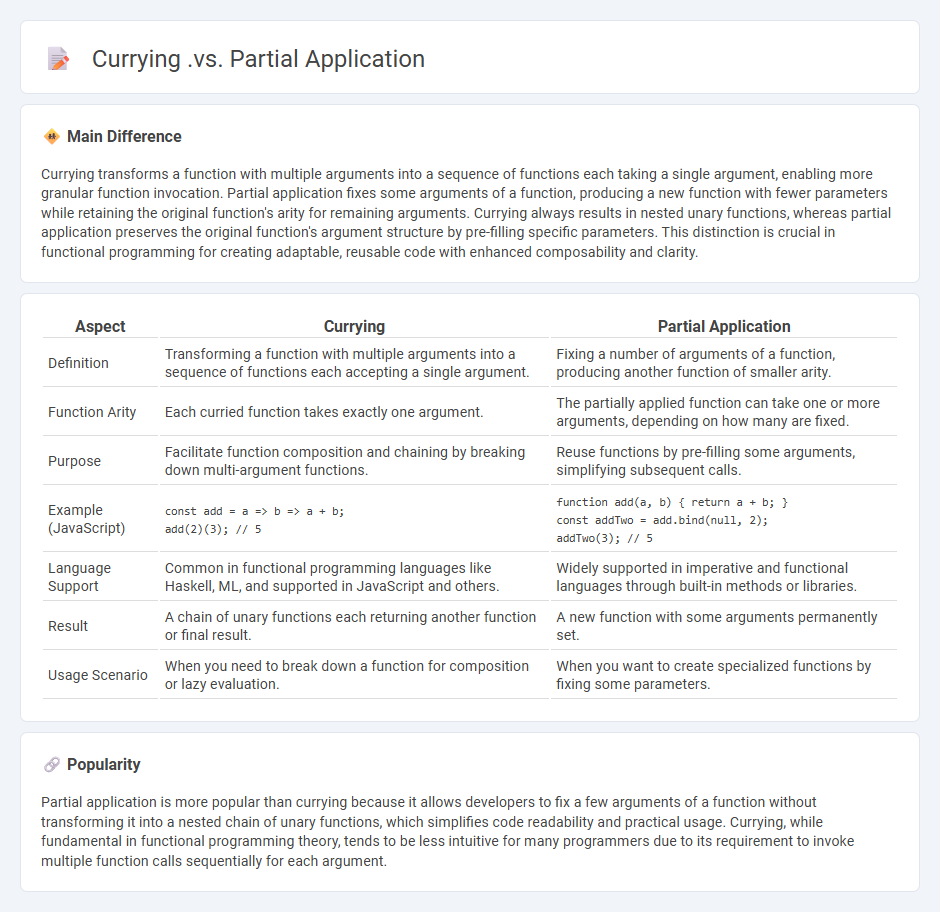
Currying transforms a function with multiple arguments into a sequence of functions each taking a single argument, enabling more granular function invocation. Partial application fixes some arguments of a function, producing a new function with fewer parameters while retaining the original function's arity for remaining arguments. Currying always results in nested unary functions, whereas partial application preserves the original function's argument structure by pre-filling specific parameters. This distinction is crucial in functional programming for creating adaptable, reusable code with enhanced composability and clarity.
Connection
Currying transforms a function with multiple arguments into a sequence of unary functions, enabling partial application by fixing some arguments and producing new functions for the remaining ones. Partial application specializes a function by pre-filling select parameters, effectively utilizing the curried form to create more specific, reusable functions. Both techniques enhance function modularity and promote code reusability in functional programming paradigms.
Comparison Table
| Aspect | Currying | Partial Application |
|---|---|---|
| Definition | Transforming a function with multiple arguments into a sequence of functions each accepting a single argument. | Fixing a number of arguments of a function, producing another function of smaller arity. |
| Function Arity | Each curried function takes exactly one argument. | The partially applied function can take one or more arguments, depending on how many are fixed. |
| Purpose | Facilitate function composition and chaining by breaking down multi-argument functions. | Reuse functions by pre-filling some arguments, simplifying subsequent calls. |
| Example (JavaScript) |
const add = a => b => a + b;add(2)(3); // 5
|
function add(a, b) { return a + b; }const addTwo = add.bind(null, 2);addTwo(3); // 5
|
| Language Support | Common in functional programming languages like Haskell, ML, and supported in JavaScript and others. | Widely supported in imperative and functional languages through built-in methods or libraries. |
| Result | A chain of unary functions each returning another function or final result. | A new function with some arguments permanently set. |
| Usage Scenario | When you need to break down a function for composition or lazy evaluation. | When you want to create specialized functions by fixing some parameters. |
Currying
Currying transforms a function with multiple arguments into a sequence of functions each taking a single argument, enhancing code modularity and reusability. Originating from the work of logician Haskell Curry, this technique is fundamental in functional programming languages such as Haskell, Scala, and JavaScript. Curried functions enable partial application, allowing developers to fix some arguments and generate new specialized functions. This approach simplifies function composition and leads to more expressive and maintainable code bases.
Partial Application
Partial application in computer science refers to the technique of fixing a few arguments of a multi-argument function, producing another function of smaller arity. This concept is widely used in functional programming languages such as Haskell and Scala to improve code reusability and modularity. Partial application enables developers to create specialized functions by pre-filling some parameters, reducing redundancy and enhancing maintainability. It differs from currying, as partial application fixes some arguments partially while currying transforms a function into a sequence of functions each with a single argument.
Higher-Order Functions
Higher-order functions are fundamental constructs in computer science, enabling functions to accept other functions as arguments or return them as results. They are extensively used in functional programming languages like Haskell, Scala, and JavaScript to facilitate code abstraction and modularity. Common examples include map, filter, and reduce functions, which operate on collections to transform or aggregate data efficiently. The use of higher-order functions enhances code reusability and supports declarative programming paradigms.
Function Arity
Function arity refers to the number of arguments or parameters that a function accepts in programming and computer science. It defines how many inputs must be provided for the function to execute correctly. Functions with fixed arity require an exact number of arguments, while variadic functions can accept a variable number of arguments. Understanding function arity is essential for function overloading, type checking, and designing APIs in languages like Java, Python, and C++.
Argument Binding
Argument binding in computer science refers to the process of associating actual argument values with formal parameters during function or procedure calls. It ensures that the inputs provided to a routine are correctly matched with the expected variables in the subroutine's definition. This mechanism is crucial for enabling correct data flow and execution within programming languages like C++, Java, and Python. Efficient argument binding enhances runtime performance and supports features such as recursion, higher-order functions, and polymorphism.
Source and External Links
Javascript - Currying VS Partial Application - Stackify - Currying transforms a function so it takes one argument at a time returning functions until all arguments are applied, while partial application fixes some arguments to produce a new function awaiting the rest.
Javascript Bind, Partial Application, and Currying - Partial application pre-fills some arguments of a function to reduce its arity, whereas currying breaks a multi-argument function into a chain of unary functions, allowing calls like add(3)(1)(4).
Functional programming in JavaScript: Currying vs partial application - Currying makes a function more flexible by transforming it into a series of unary functions for composition, while partial application creates specialized functions by fixing some of the original function's arguments.
FAQs
What is currying in programming?
Currying in programming transforms a function with multiple arguments into a sequence of functions each taking a single argument.
What is partial application?
Partial application is a functional programming technique where a function is fixed with some arguments, producing a new function that takes the remaining arguments.
How does currying differ from partial application?
Currying transforms a function with multiple arguments into a sequence of functions each taking a single argument, while partial application fixes some arguments of a function producing another function with fewer arguments.
What are the benefits of currying?
Currying enables partial function application, improves code reusability, enhances function composition, simplifies argument handling, and promotes functional programming paradigms.
What are some real-world examples of partial application?
In JavaScript, using `bind()` to fix initial function arguments; in Python, employing `functools.partial` to preset function parameters; in Haskell, supplying fewer arguments than required to a function, creating a new function awaiting the remaining arguments.
When should you use currying instead of partial application?
Use currying when you need to transform a function with multiple arguments into a sequence of unary functions for better function composition and reuse; use partial application when you want to fix some arguments of a function to create a new function with fewer parameters for specific use cases.
Can currying and partial application be combined?
Yes, currying and partial application can be combined by first converting a multi-argument function into a sequence of unary functions (currying) and then applying some of these unary functions with specific arguments (partial application) to create specialized functions.
 calledges.com
calledges.com