The Archimedean spiral features a constant distance between successive turns, characterized mathematically by the equation r = a + bth, where r is the radius and th is the angle. In contrast, the logarithmic spiral expands exponentially with the radius increasing as r = ae^{bth}, resulting in distinctive self-similar patterns seen in nature, such as nautilus shells and galaxies. Explore the unique mathematical properties and applications of these spirals to understand their pivotal roles in science and art.
Main Difference
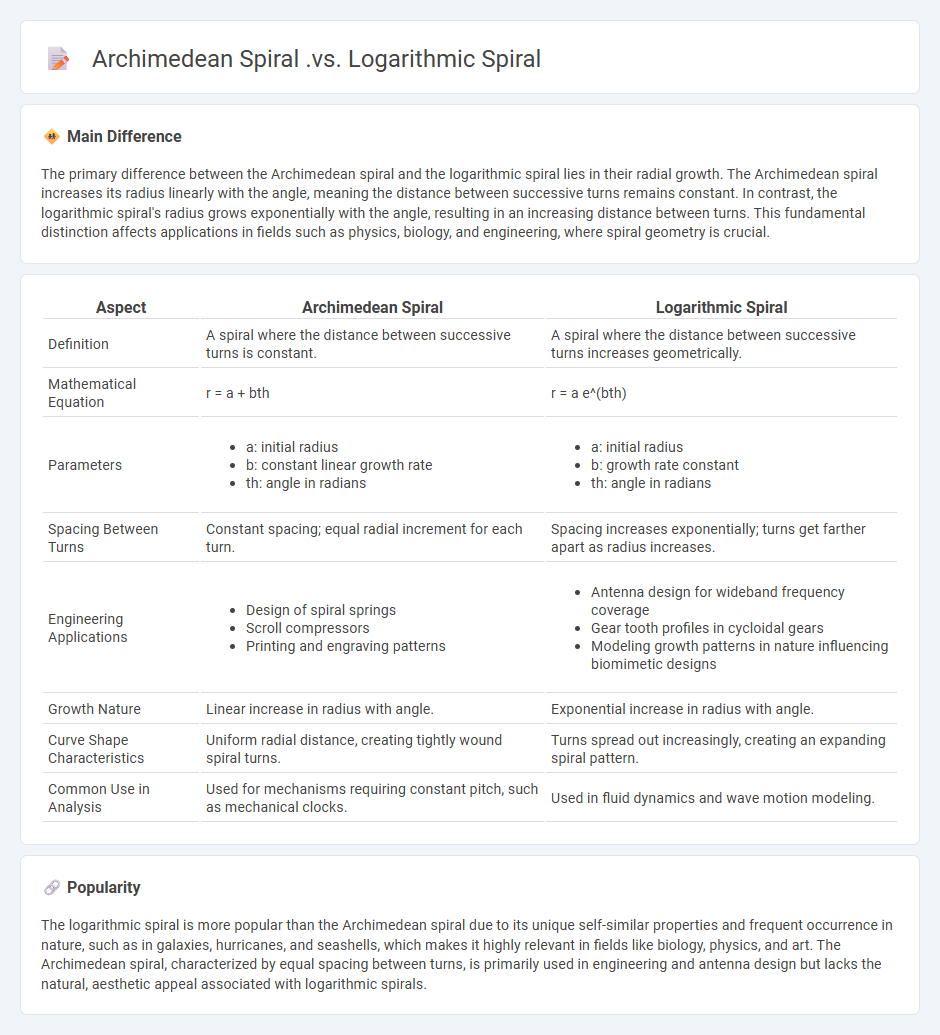
The primary difference between the Archimedean spiral and the logarithmic spiral lies in their radial growth. The Archimedean spiral increases its radius linearly with the angle, meaning the distance between successive turns remains constant. In contrast, the logarithmic spiral's radius grows exponentially with the angle, resulting in an increasing distance between turns. This fundamental distinction affects applications in fields such as physics, biology, and engineering, where spiral geometry is crucial.
Connection
The Archimedean spiral and logarithmic spiral share the property of being plane curves generated by points moving away from a fixed center, but they differ in their growth patterns: the Archimedean spiral increases its distance from the center linearly with respect to the angle, while the logarithmic spiral grows exponentially. Both spirals have applications in physics, engineering, and nature, such as modeling wave patterns and the structure of galaxies. The mathematical relationship between them highlights distinct geometric properties used for optimizing design and analysis in various scientific fields.
Comparison Table
| Aspect | Archimedean Spiral | Logarithmic Spiral |
|---|---|---|
| Definition | A spiral where the distance between successive turns is constant. | A spiral where the distance between successive turns increases geometrically. |
| Mathematical Equation | r = a + bth | r = a e^(bth) |
| Parameters |
|
|
| Spacing Between Turns | Constant spacing; equal radial increment for each turn. | Spacing increases exponentially; turns get farther apart as radius increases. |
| Engineering Applications |
|
|
| Growth Nature | Linear increase in radius with angle. | Exponential increase in radius with angle. |
| Curve Shape Characteristics | Uniform radial distance, creating tightly wound spiral turns. | Turns spread out increasingly, creating an expanding spiral pattern. |
| Common Use in Analysis | Used for mechanisms requiring constant pitch, such as mechanical clocks. | Used in fluid dynamics and wave motion modeling. |
Growth Rate
The growth rate in engineering reflects the sector's rapid expansion driven by technological advancements and increased infrastructure investments. Data from the U.S. Bureau of Labor Statistics projects a 4% employment growth rate for civil engineers from 2022 to 2032, faster than the average for all occupations. The rise of renewable energy projects and smart infrastructure contributes significantly to job creation and innovation. Emphasis on sustainable design and automation further accelerates demand for engineering expertise worldwide.
Curve Equation
The curve equation in engineering typically represents mathematical functions that describe the shape and behavior of curves used in design and analysis. Common forms include polynomial, parametric, and spline equations, each tailored to specific applications such as structural modeling, fluid dynamics, or aerodynamics. Precision in these equations ensures accurate simulations and performance predictions for engineering projects. Examples include Bezier curves for computer-aided design and clothoid curves in transportation engineering.
Mechanical Design
Mechanical design involves the application of engineering principles to create and analyze physical components and systems that perform specific functions. It integrates material science, mechanics, and manufacturing processes to ensure structural integrity, efficiency, and durability. Common tools in mechanical design include CAD software like SolidWorks and AutoCAD, enabling precise modeling and simulation. Key industries leveraging mechanical design range from automotive and aerospace to robotics and consumer electronics.
Fluid Dynamics
Fluid dynamics, a crucial subfield of engineering, explores the behavior of liquids and gases in motion, essential for designing efficient systems in aerospace, automotive, and civil engineering. It encompasses the study of laminar and turbulent flows, governed by the Navier-Stokes equations, enabling precise modeling of airflow around aircraft wings or water flow in pipelines. Advanced computational fluid dynamics (CFD) tools simulate complex fluid interactions, optimizing performance and reducing energy consumption in engineering projects. Understanding fluid mechanics principles directly impacts the development of renewable energy technologies, such as wind turbines and hydroelectric power plants.
Stress Distribution
Stress distribution in engineering refers to how internal forces are spread within a material or structural component under load. Understanding this distribution is crucial for predicting failure points and ensuring structural integrity in designs such as beams, bridges, and aircraft frames. Engineers use computational methods like finite element analysis (FEA) to model stress patterns accurately in complex geometries and varied loading conditions. Optimizing stress distribution improves material efficiency and enhances safety in engineering applications.
Source and External Links
Logarithmic spiral - Wikipedia - The logarithmic spiral is a self-similar curve where the distances between successive turnings increase in a geometric progression, described by \( r = a e^{k\varphi} \) in polar coordinates.
Archimedean spiral - MATHCURVE.COM - The Archimedean spiral features constant separation between successive turnings, so any ray from the origin intersects the spiral at points with a fixed distance apart, described by \( r = a\varphi \) in polar coordinates.
Spirals in Nature - Life Through A Mathematician's Eyes - While both spirals appear in nature, the logarithmic spiral is more common (e.g., nautilus shells, galaxies), whereas the Archimedean spiral is rarer but can be seen in ferns, fingerprints, and some plant structures.
FAQs
What is a spiral in geometry?
A spiral in geometry is a curve that continuously moves away from a fixed point while rotating around it.
What is an Archimedean spiral?
An Archimedean spiral is a curve defined by the polar equation r = a + bth, where the distance between successive turns is constant.
What is a logarithmic spiral?
A logarithmic spiral is a self-similar curve that expands exponentially with a constant angle between the radius vector and the tangent, defined mathematically by the polar equation r = ae^(bth).
How do Archimedean and logarithmic spirals differ mathematically?
Archimedean spirals have a linear radial growth defined by r = a + bth, while logarithmic spirals exhibit exponential radial growth described by r = ae^(bth).
Where are Archimedean spirals found in nature or engineering?
Archimedean spirals are found in nature in sunflower seed patterns, snail shells, and galaxies, and in engineering they are used in antenna design, rotary compressors, and spiral staircases.
Where are logarithmic spirals observed in the real world?
Logarithmic spirals are observed in seashells, hurricanes, galaxies, sunflower seed patterns, and animal horns.
Why do logarithmic spirals appear in natural phenomena more often than Archimedean spirals?
Logarithmic spirals appear more often in natural phenomena because their shape scales exponentially, allowing consistent pattern growth without changing form, which matches biological growth processes and physical forces, whereas Archimedean spirals increase linearly and do not accommodate self-similar scaling.
 calledges.com
calledges.com