Modal analysis identifies the natural frequencies and mode shapes of structures to predict resonant behavior under dynamic loading. Harmonic analysis evaluates the steady-state response of structures subjected to sinusoidal loads at varying frequencies, crucial for understanding vibration amplitudes and stresses. Explore detailed comparisons to optimize engineering designs and enhance structural performance.
Main Difference
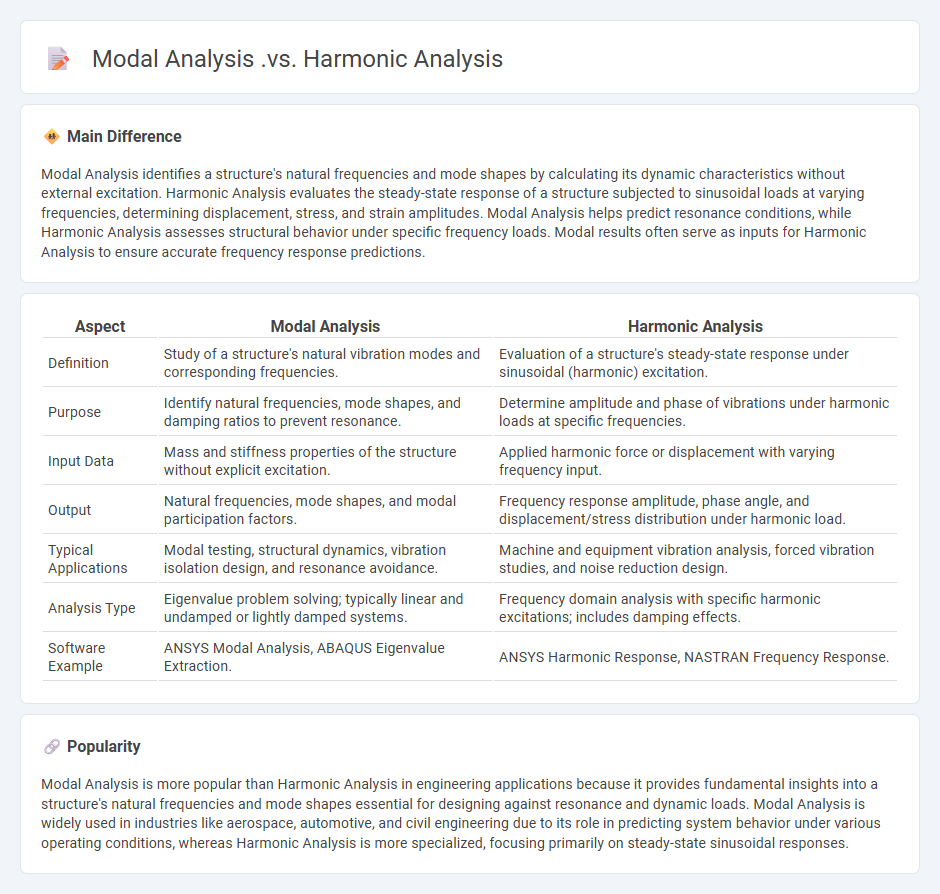
Modal Analysis identifies a structure's natural frequencies and mode shapes by calculating its dynamic characteristics without external excitation. Harmonic Analysis evaluates the steady-state response of a structure subjected to sinusoidal loads at varying frequencies, determining displacement, stress, and strain amplitudes. Modal Analysis helps predict resonance conditions, while Harmonic Analysis assesses structural behavior under specific frequency loads. Modal results often serve as inputs for Harmonic Analysis to ensure accurate frequency response predictions.
Connection
Modal analysis identifies natural frequencies and mode shapes of a structure, which serve as critical input parameters for harmonic analysis to predict dynamic response under sinusoidal loading. Harmonic analysis uses these modal properties to efficiently compute steady-state vibration amplitudes at specific excitation frequencies. The integration of modal analysis results into harmonic analysis enhances accuracy in predicting resonance and structural behavior in engineering applications.
Comparison Table
| Aspect | Modal Analysis | Harmonic Analysis |
|---|---|---|
| Definition | Study of a structure's natural vibration modes and corresponding frequencies. | Evaluation of a structure's steady-state response under sinusoidal (harmonic) excitation. |
| Purpose | Identify natural frequencies, mode shapes, and damping ratios to prevent resonance. | Determine amplitude and phase of vibrations under harmonic loads at specific frequencies. |
| Input Data | Mass and stiffness properties of the structure without explicit excitation. | Applied harmonic force or displacement with varying frequency input. |
| Output | Natural frequencies, mode shapes, and modal participation factors. | Frequency response amplitude, phase angle, and displacement/stress distribution under harmonic load. |
| Typical Applications | Modal testing, structural dynamics, vibration isolation design, and resonance avoidance. | Machine and equipment vibration analysis, forced vibration studies, and noise reduction design. |
| Analysis Type | Eigenvalue problem solving; typically linear and undamped or lightly damped systems. | Frequency domain analysis with specific harmonic excitations; includes damping effects. |
| Software Example | ANSYS Modal Analysis, ABAQUS Eigenvalue Extraction. | ANSYS Harmonic Response, NASTRAN Frequency Response. |
Natural Frequencies
Natural frequencies are intrinsic oscillation rates at which engineering structures and mechanical systems vibrate when subjected to dynamic forces. These frequencies depend on the system's material properties, geometry, and boundary conditions, playing a critical role in designing bridges, buildings, and machinery. Identifying natural frequencies helps prevent resonance, which can cause catastrophic failures due to excessive vibrations. Modal analysis and finite element methods are commonly used techniques to calculate and optimize natural frequency responses in engineering applications.
Mode Shapes
Mode shapes in engineering define the characteristic patterns of deformation that structures undergo at specific natural frequencies during vibration. These shapes are critical for understanding how buildings, bridges, and mechanical components respond to dynamic loads and for predicting potential resonance phenomena. Computational methods like finite element analysis (FEA) enable precise mode shape determination, facilitating design optimization and failure prevention. Engineers rely on mode shape analysis to enhance structural integrity and ensure safety under operational and seismic conditions.
Forced Vibration
Forced vibration occurs when an external periodic force influences a mechanical system, causing it to oscillate at the frequency of the applied force. This phenomenon is critical in engineering fields such as structural, mechanical, and aerospace engineering, where understanding system response to dynamic loads ensures stability and longevity. Engineers analyze forced vibration through differential equations of motion and apply concepts like damping, resonance, and steady-state response to design systems that minimize unwanted oscillations. Accurate modeling helps in predicting behavior under varying frequencies, preventing failures due to resonance amplification.
Frequency Response
Frequency response measures how an engineering system, such as electrical circuits or mechanical structures, reacts to varying input signal frequencies. It characterizes the amplitude and phase relationship between input and output signals across a frequency spectrum, typically represented by Bode plots or Nyquist diagrams. Accurate frequency response analysis is essential for designing stable control systems, filters, and vibration isolators, ensuring optimal performance and minimal distortion. Tools like network analyzers and software simulations provide precise frequency response measurements in engineering applications.
Damping
Damping in engineering refers to the process of reducing the amplitude of vibrations or oscillations in mechanical systems through energy dissipation. Common types include viscous damping, where a fluid provides resistance, and structural damping, which arises from internal friction within materials. Effective damping improves the stability and longevity of structures such as bridges, machinery, and automotive suspensions by minimizing resonance and fatigue. Engineers often use materials like rubber or design elements like tuned mass dampers to optimize damping performance.
Source and External Links
Modal & Harmonic Response Analysis | PPTX - Modal analysis finds natural frequencies and mode shapes of a structure under vibration to understand deformation patterns, while harmonic analysis calculates steady-state responses to sinusoidal loads at different frequencies based on those modal results.
Modal analysis and harmonic response - Modal analysis determines an object's natural vibration modes and frequencies during free vibration; harmonic response analysis simulates the vibrational behavior due to specific excitations at varying frequencies.
Modal and Harmonic Analysis of Master Leaf Spring - Modal analysis studies natural frequencies and mode shapes in free vibration, while harmonic analysis finds the steady-state response of a structure subjected to sinusoidally varying loads, especially important to assess resonance risks.
FAQs
What is modal analysis?
Modal analysis is the study of a structure's natural vibration frequencies, mode shapes, and damping characteristics to predict its dynamic response.
What is harmonic analysis?
Harmonic analysis is the mathematical study of representing functions or signals as the superposition of basic waves, typically involving Fourier series and Fourier transforms.
How does modal analysis differ from harmonic analysis?
Modal analysis determines a structure's natural frequencies and mode shapes by evaluating its dynamic characteristics without external loads, while harmonic analysis assesses steady-state response under sinusoidal excitation at varying frequencies to predict vibration amplitude and stress.
What are the applications of modal analysis?
Modal analysis is applied in structural engineering for identifying vibration characteristics, in automotive and aerospace industries for optimizing dynamic performance, in civil engineering to assess earthquake resistance, and in mechanical design to prevent resonance-related failures.
What are the applications of harmonic analysis?
Harmonic analysis is applied in signal processing, image compression, quantum mechanics, acoustics, vibration analysis, medical imaging (e.g., MRI), wireless communications, and data science for pattern recognition and time-series analysis.
What data does modal analysis provide?
Modal analysis provides natural frequencies, mode shapes, and damping ratios of a structure or system.
What results can you obtain from harmonic analysis?
Harmonic analysis decomposes functions into basic waves, identifies frequency components, analyzes signal properties, solves differential equations, and studies patterns in data and structures.
 calledges.com
calledges.com