Shear stress arises when forces act parallel to a material's surface, causing layers to slide past one another, while tensile stress occurs when forces pull perpendicular to the surface, stretching the material. Understanding the differences between shear stress and tensile stress is crucial for predicting material behavior under various loading conditions in engineering and design applications. Explore more about how these stresses influence structural integrity and material performance.
Main Difference
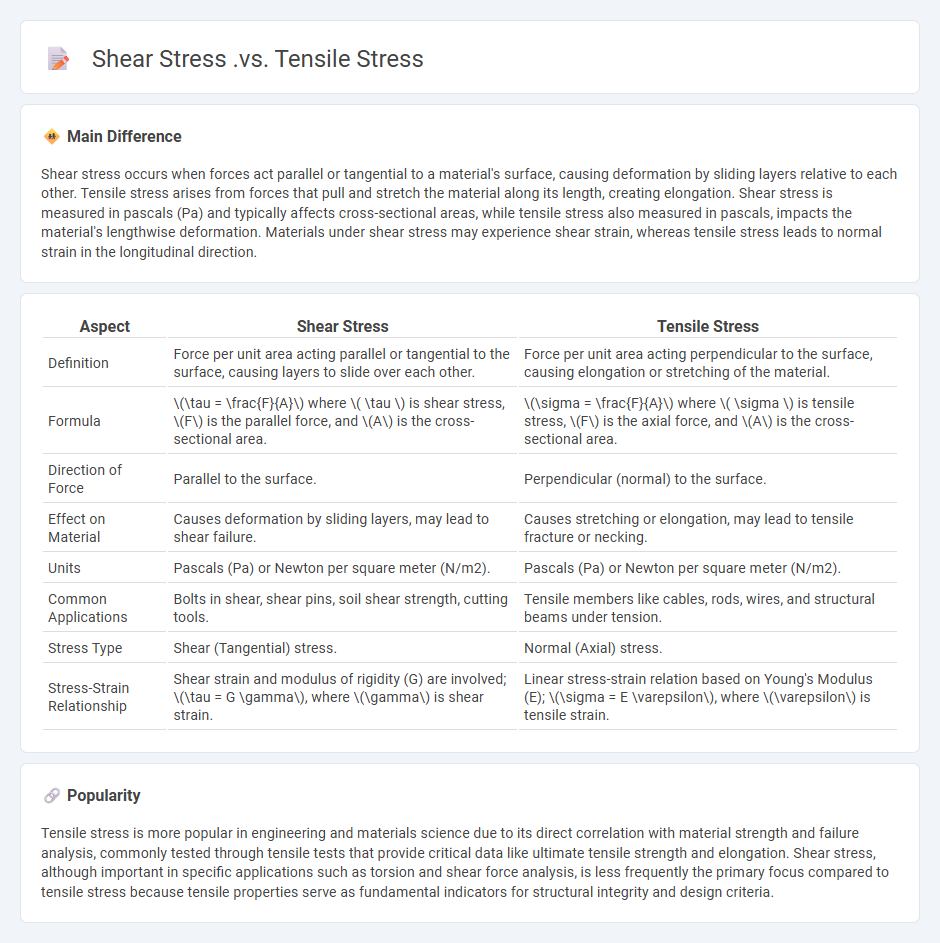
Shear stress occurs when forces act parallel or tangential to a material's surface, causing deformation by sliding layers relative to each other. Tensile stress arises from forces that pull and stretch the material along its length, creating elongation. Shear stress is measured in pascals (Pa) and typically affects cross-sectional areas, while tensile stress also measured in pascals, impacts the material's lengthwise deformation. Materials under shear stress may experience shear strain, whereas tensile stress leads to normal strain in the longitudinal direction.
Connection
Shear stress and tensile stress are connected through their influence on material deformation and failure mechanisms. Tensile stress acts perpendicular to the cross-sectional area, causing elongation, while shear stress acts parallel, causing sliding between material layers. Understanding their interaction is crucial for predicting failure modes and ensuring structural integrity in engineering applications.
Comparison Table
| Aspect | Shear Stress | Tensile Stress |
|---|---|---|
| Definition | Force per unit area acting parallel or tangential to the surface, causing layers to slide over each other. | Force per unit area acting perpendicular to the surface, causing elongation or stretching of the material. |
| Formula | \(\tau = \frac{F}{A}\) where \( \tau \) is shear stress, \(F\) is the parallel force, and \(A\) is the cross-sectional area. | \(\sigma = \frac{F}{A}\) where \( \sigma \) is tensile stress, \(F\) is the axial force, and \(A\) is the cross-sectional area. |
| Direction of Force | Parallel to the surface. | Perpendicular (normal) to the surface. |
| Effect on Material | Causes deformation by sliding layers, may lead to shear failure. | Causes stretching or elongation, may lead to tensile fracture or necking. |
| Units | Pascals (Pa) or Newton per square meter (N/m2). | Pascals (Pa) or Newton per square meter (N/m2). |
| Common Applications | Bolts in shear, shear pins, soil shear strength, cutting tools. | Tensile members like cables, rods, wires, and structural beams under tension. |
| Stress Type | Shear (Tangential) stress. | Normal (Axial) stress. |
| Stress-Strain Relationship | Shear strain and modulus of rigidity (G) are involved; \(\tau = G \gamma\), where \(\gamma\) is shear strain. | Linear stress-strain relation based on Young's Modulus (E); \(\sigma = E \varepsilon\), where \(\varepsilon\) is tensile strain. |
Shear Stress
Shear stress in engineering refers to the force per unit area exerted parallel to the surface of a material. It is measured in Pascals (Pa) or pounds per square inch (psi) and plays a crucial role in the design of mechanical components such as beams, shafts, and fasteners. Understanding shear stress distribution helps engineers predict material failure modes like shear deformation and fractures. Accurate calculation of shear stress is essential for ensuring structural integrity and safety in civil, mechanical, and aerospace engineering projects.
Tensile Stress
Tensile stress measures the internal force per unit area experienced by a material when subjected to a pulling or stretching load. It is calculated by dividing the applied tensile force by the original cross-sectional area of the specimen, typically expressed in pascals (Pa) or megapascals (MPa). Commonly used in structural engineering and material science, tensile stress helps evaluate the strength and ductility of metals, polymers, and composites. Understanding tensile stress is crucial for designing safe and efficient bridges, aircraft components, and mechanical parts under axial loads.
Material Deformation
Material deformation in engineering refers to the alteration of an object's shape or size under applied forces or stresses, encompassing elastic, plastic, and viscoelastic behaviors. Understanding stress-strain relationships through models such as Hooke's Law and plasticity theory is critical for designing durable structures. Key parameters influencing deformation include yield strength, Young's modulus, and Poisson's ratio, which vary significantly among metals, polymers, and composites. Advanced computational methods like finite element analysis enable precise simulation of deformation patterns to optimize engineering materials and components.
Failure Modes
Failure modes in engineering refer to the various ways a system, component, or material can fail to perform its intended function. Common failure modes include fatigue, corrosion, wear, fracture, and thermal degradation, each impacting reliability and safety differently. Engineers use Failure Mode and Effects Analysis (FMEA) to identify potential failure points and mitigate risks proactively. Understanding failure characteristics enables optimization of design, maintenance schedules, and material selection to enhance system durability.
Load Direction
Load direction in engineering refers to the specific orientation or path along which forces are applied to a structure or material. Understanding load direction is crucial for accurately predicting structural responses, such as stress, strain, and deformation. Engineers use techniques like finite element analysis (FEA) to model how different load directions impact stability and safety. Proper assessment of load direction ensures optimized design and prevents failure in applications ranging from aerospace to civil infrastructure.
Source and External Links
Tensile Stress & Strain, Compressive Stress & Shear Stress - Tensile stress occurs when two forces pull an object, stretching it and increasing its length, while shear stress happens when forces are applied parallel to the surface, causing the material to deform sideways.
Tensile Compressive Shear - Tensile stress is the result of pulling on the ends of a bar, elongating it, whereas shear stress occurs when forces are applied in opposite directions on adjacent surfaces, resulting in a sliding or twisting deformation.
Tensile, Compressive, Shear, and Torsional Stress - Tensile stress is a stretching force acting perpendicular to the cross-sectional area, while shear stress is a force acting parallel to the cross-section, causing one part to slip relative to the adjacent part.
FAQs
What is stress in materials science?
Stress in materials science is the internal force per unit area within a material that arises from externally applied forces, measured in pascals (Pa).
What is the difference between shear stress and tensile stress?
Shear stress acts parallel to the material surface causing deformation by sliding layers, while tensile stress acts perpendicular, stretching the material and causing elongation.
How is shear stress measured?
Shear stress is measured using a shear stress sensor or rheometer by applying a known force parallel to the surface area and dividing the force by that area, typically expressed in pascals (Pa).
How is tensile stress calculated?
Tensile stress is calculated by dividing the tensile force (F) applied to an object by the cross-sectional area (A) of the object, using the formula: \(\sigma = \frac{F}{A}\), where \(\sigma\) is tensile stress in pascals (Pa), F is force in newtons (N), and A is area in square meters (m2).
What are examples of shear stress in real life?
Examples of shear stress in real life include cutting paper with scissors, sliding a deck of cards, stress on bridge beams under traffic loads, and shearing forces in turbines and gears.
Where do you find tensile stress in engineering applications?
Tensile stress is found in engineering applications such as cables, beams under tension, structural rods, bridges, cranes, and tension members of trusses.
Why is understanding the difference between shear and tensile stress important?
Understanding the difference between shear and tensile stress is crucial for designing structures and materials that can withstand specific forces, ensuring safety, durability, and performance by accurately predicting failure modes and selecting appropriate materials.
 calledges.com
calledges.com