Finite Element Analysis (FEA) and Boundary Element Method (BEM) are computational techniques widely used in engineering and physics for solving complex structural, thermal, and fluid problems. FEA discretizes the entire volume into finite elements, making it ideal for heterogeneous materials and nonlinear problems, while BEM reduces the problem dimensionality by focusing on boundaries, offering efficiency in problems with infinite domains. Explore deeper into their comparative advantages and applications to determine the best approach for your specific engineering challenges.
Main Difference
Finite Element Analysis (FEA) discretizes the entire problem domain into small elements, enabling detailed modeling of complex geometries and material behaviors, ideal for nonlinear and heterogeneous materials. Boundary Element Method (BEM) discretizes only the boundary surfaces, significantly reducing dimensionality and computational resources for problems with infinite or semi-infinite domains, especially in linear and homogeneous materials. FEA typically requires more computational power and memory due to volume meshing, while BEM advantageously handles problems with less complex domain requirements but can become cumbersome with nonlinearities. The choice between FEA and BEM depends on problem geometry, material properties, and computational efficiency needs.
Connection
Finite Element Analysis (FEA) and Boundary Element Method (BEM) are connected through their shared goal of solving complex engineering problems by approximating solutions to partial differential equations. FEA discretizes the entire problem domain into finite elements, making it suitable for nonlinear and heterogeneous materials, while BEM reduces the problem dimensionality by only discretizing boundaries, which is advantageous for infinite or semi-infinite domains. Both methods complement each other in multi-physics simulations, enabling efficient and accurate modeling of structural, thermal, and fluid dynamics problems.
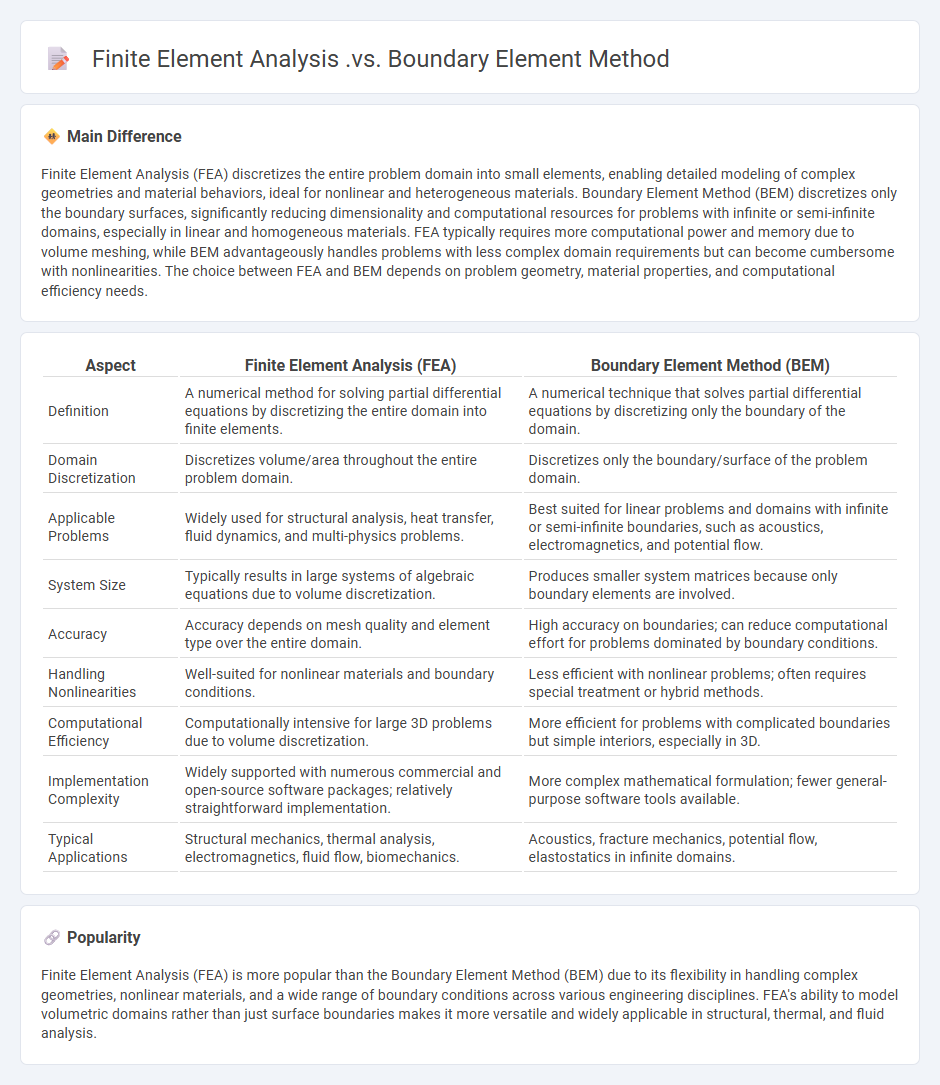
Comparison Table
| Aspect | Finite Element Analysis (FEA) | Boundary Element Method (BEM) |
|---|---|---|
| Definition | A numerical method for solving partial differential equations by discretizing the entire domain into finite elements. | A numerical technique that solves partial differential equations by discretizing only the boundary of the domain. |
| Domain Discretization | Discretizes volume/area throughout the entire problem domain. | Discretizes only the boundary/surface of the problem domain. |
| Applicable Problems | Widely used for structural analysis, heat transfer, fluid dynamics, and multi-physics problems. | Best suited for linear problems and domains with infinite or semi-infinite boundaries, such as acoustics, electromagnetics, and potential flow. |
| System Size | Typically results in large systems of algebraic equations due to volume discretization. | Produces smaller system matrices because only boundary elements are involved. |
| Accuracy | Accuracy depends on mesh quality and element type over the entire domain. | High accuracy on boundaries; can reduce computational effort for problems dominated by boundary conditions. |
| Handling Nonlinearities | Well-suited for nonlinear materials and boundary conditions. | Less efficient with nonlinear problems; often requires special treatment or hybrid methods. |
| Computational Efficiency | Computationally intensive for large 3D problems due to volume discretization. | More efficient for problems with complicated boundaries but simple interiors, especially in 3D. |
| Implementation Complexity | Widely supported with numerous commercial and open-source software packages; relatively straightforward implementation. | More complex mathematical formulation; fewer general-purpose software tools available. |
| Typical Applications | Structural mechanics, thermal analysis, electromagnetics, fluid flow, biomechanics. | Acoustics, fracture mechanics, potential flow, elastostatics in infinite domains. |
Discretization Approach
Discretization in engineering transforms continuous models, equations, or signals into discrete counterparts to facilitate numerical analysis and simulation. Common methods include finite difference, finite element, and finite volume techniques, widely applied in structural analysis, fluid dynamics, and control systems. This approach enables computer-based solutions to partial differential equations governing physical phenomena, improving accuracy and computational efficiency. Discretization bridges the gap between theoretical models and practical engineering applications by enabling precise numerical approximations.
Domain vs Boundary Modeling
Domain modeling focuses on representing the core concepts, entities, and relationships within a specific problem area to accurately reflect business logic and requirements. Boundary modeling defines the interfaces and interaction points between the system and external actors or systems, ensuring clear communication and integration. Effective engineering practices combine domain models with boundary models to create well-structured, maintainable software architectures. These models help in isolating internal complexities from external concerns, enhancing modularity and scalability in engineering projects.
Computational Efficiency
Computational efficiency in engineering focuses on optimizing algorithms and system designs to reduce processing time and resource consumption. Techniques such as parallel processing, hardware acceleration, and algorithmic optimization enable faster simulations and real-time data analysis. Efficient computation directly impacts the development of complex systems like aerospace vehicles, robotics, and structural engineering models. This optimization leads to cost savings, improved performance, and enhanced decision-making in engineering projects.
Complex Geometry Handling
Complex geometry handling in engineering involves advanced software tools such as CAD (Computer-Aided Design) and CAE (Computer-Aided Engineering) systems that enable precise modeling of intricate shapes and structures. Techniques like mesh generation and finite element analysis (FEA) allow engineers to simulate physical behaviors and optimize designs with high accuracy. Industries including aerospace, automotive, and civil engineering rely on these methods to address challenges posed by non-standard geometries and ensure structural integrity. Integration of parametric design and 3D printing further enhances the ability to manage complex geometries efficiently.
Typical Engineering Applications
Engineering applications span diverse fields such as civil, mechanical, electrical, and chemical engineering, addressing infrastructure, machinery design, power systems, and industrial processes. Civil engineering focuses on constructing roads, bridges, and buildings, ensuring safety and sustainability through advanced materials and structural analysis. Mechanical engineering involves the design and manufacturing of engines, HVAC systems, and robotics, emphasizing thermodynamics and material science. Electrical engineering covers power generation, circuit design, and telecommunications, while chemical engineering optimizes chemical reactions for pharmaceuticals, petrochemicals, and environmental solutions.
Source and External Links
comparative efficiency of finite, boundary, and hybrid element ... - For interior problems, some studies find Boundary Element Method (BEM) more effective than Finite Element Method (FEM), while others find the opposite; for exterior problems, BEM is sometimes more effective, but results are inconsistent and depend heavily on the problem type.
BEM vs FEM | INTEGRATED Engineering Software - BEM solves for unknowns only on boundaries, requiring discretization of active regions, while FEM solves for unknowns throughout the entire volume, demanding full geometry modeling; BEM can be more efficient for field problems where only boundary behavior matters.
Numerical Modeling: Boundary Method vs. Finite Element Method - BEM is advantageous for problems with complicated boundaries and requires only surface discretization, but its suitability and accuracy depend on available fundamental solutions; FEM is more flexible for nonlinear, inhomogeneous, or volume-dominated problems but requires meshing the entire domain.
FAQs
What is Finite Element Analysis?
Finite Element Analysis (FEA) is a computational method that divides complex structures into smaller elements to predict their behavior under various physical conditions such as stress, heat, and vibration.
What is the Boundary Element Method?
The Boundary Element Method (BEM) is a numerical computational technique used to solve linear partial differential equations by transforming them into integral equations defined only on the problem's boundary.
How do FEA and BEM differ in mathematical approach?
FEA divides the domain into discrete elements using volume discretization to approximate PDEs numerically, while BEM reduces problem dimensionality by formulating boundary integral equations solved only on the domain boundary.
What are the advantages of Finite Element Analysis?
Finite Element Analysis offers precise simulation of complex structures, reduces physical prototype costs, enables stress and thermal analysis under varied conditions, improves product design efficiency, and supports optimization in engineering and manufacturing processes.
What are the benefits of the Boundary Element Method?
The benefits of the Boundary Element Method (BEM) include reduced dimensionality in problem modeling, fewer elements required for meshing since only boundaries are discretized, higher accuracy in modeling infinite or semi-infinite domains, and efficient handling of problems with complex geometries and boundary conditions.
When should you use FEA instead of BEM?
Use Finite Element Analysis (FEA) instead of Boundary Element Method (BEM) when dealing with complex material heterogeneity, nonlinear behavior, and volumetric domain problems requiring detailed internal stress and strain analysis.
What are the limitations of Boundary Element Method compared to FEA?
Boundary Element Method (BEM) has limitations including difficulty handling nonlinear and inhomogeneous materials, complexity in modeling multi-domain problems, and denser system matrices leading to higher computational costs for large-scale problems, whereas Finite Element Analysis (FEA) more easily addresses these issues with volumetric discretization.
 calledges.com
calledges.com