PID control utilizes proportional, integral, and derivative terms to maintain system stability and minimize error through precise mathematical adjustments. Fuzzy logic control employs rule-based systems and linguistic variables to handle uncertainty and approximate reasoning in complex or nonlinear processes. Explore deeper insights into the advantages and applications of PID versus fuzzy logic control methodologies.
Main Difference
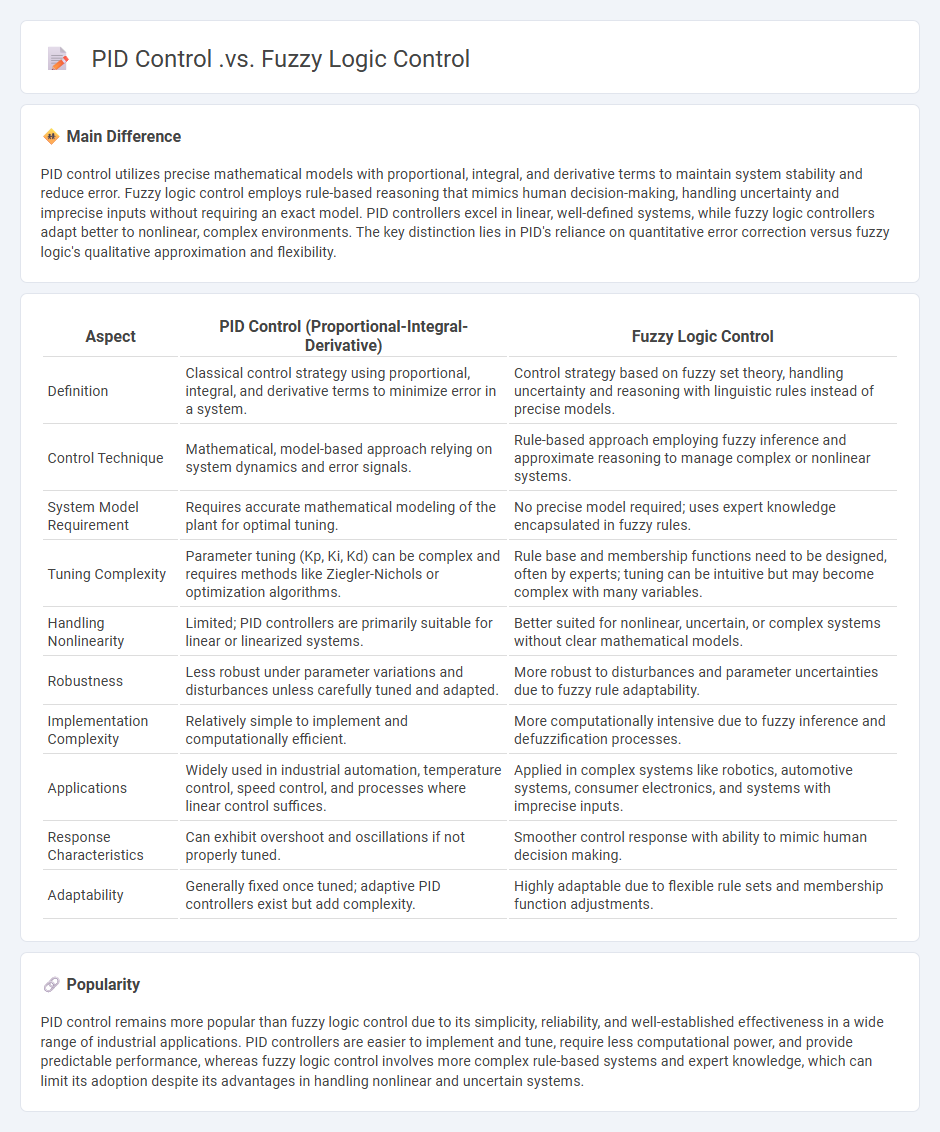
PID control utilizes precise mathematical models with proportional, integral, and derivative terms to maintain system stability and reduce error. Fuzzy logic control employs rule-based reasoning that mimics human decision-making, handling uncertainty and imprecise inputs without requiring an exact model. PID controllers excel in linear, well-defined systems, while fuzzy logic controllers adapt better to nonlinear, complex environments. The key distinction lies in PID's reliance on quantitative error correction versus fuzzy logic's qualitative approximation and flexibility.
Connection
PID control and fuzzy logic control are connected through their shared goal of regulating system behavior by adjusting control inputs based on error signals. Fuzzy logic control often incorporates elements of PID control by interpreting linguistic rules that mimic PID parameter tuning, enhancing adaptability in non-linear or uncertain environments. Both approaches aim to maintain system stability and improve performance, with fuzzy logic providing a flexible framework for handling imprecision and system complexity.
Comparison Table
| Aspect | PID Control (Proportional-Integral-Derivative) | Fuzzy Logic Control |
|---|---|---|
| Definition | Classical control strategy using proportional, integral, and derivative terms to minimize error in a system. | Control strategy based on fuzzy set theory, handling uncertainty and reasoning with linguistic rules instead of precise models. |
| Control Technique | Mathematical, model-based approach relying on system dynamics and error signals. | Rule-based approach employing fuzzy inference and approximate reasoning to manage complex or nonlinear systems. |
| System Model Requirement | Requires accurate mathematical modeling of the plant for optimal tuning. | No precise model required; uses expert knowledge encapsulated in fuzzy rules. |
| Tuning Complexity | Parameter tuning (Kp, Ki, Kd) can be complex and requires methods like Ziegler-Nichols or optimization algorithms. | Rule base and membership functions need to be designed, often by experts; tuning can be intuitive but may become complex with many variables. |
| Handling Nonlinearity | Limited; PID controllers are primarily suitable for linear or linearized systems. | Better suited for nonlinear, uncertain, or complex systems without clear mathematical models. |
| Robustness | Less robust under parameter variations and disturbances unless carefully tuned and adapted. | More robust to disturbances and parameter uncertainties due to fuzzy rule adaptability. |
| Implementation Complexity | Relatively simple to implement and computationally efficient. | More computationally intensive due to fuzzy inference and defuzzification processes. |
| Applications | Widely used in industrial automation, temperature control, speed control, and processes where linear control suffices. | Applied in complex systems like robotics, automotive systems, consumer electronics, and systems with imprecise inputs. |
| Response Characteristics | Can exhibit overshoot and oscillations if not properly tuned. | Smoother control response with ability to mimic human decision making. |
| Adaptability | Generally fixed once tuned; adaptive PID controllers exist but add complexity. | Highly adaptable due to flexible rule sets and membership function adjustments. |
Control Accuracy
Control accuracy in engineering refers to the precision with which a control system maintains a desired output within specified tolerances. High control accuracy is critical in applications such as robotics, aerospace, and manufacturing, where precise movement and positioning affect overall system performance. Techniques like PID control, model predictive control, and sensor feedback integration enhance accuracy by minimizing errors and disturbances. Standards such as ISO 9001 and IEEE guidelines often dictate acceptable accuracy levels for various engineering control systems.
System Nonlinearity
System nonlinearity in engineering refers to the behavior of systems where the output is not directly proportional to the input, often described by nonlinear differential equations. This phenomenon significantly impacts control system design, signal processing, and mechanical systems, requiring specialized analytical and numerical methods for accurate modeling and prediction. Real-world examples include robotic arm dynamics, electrical circuits with semiconductor devices, and aerodynamic forces on aircraft. Understanding nonlinearity is essential for enhancing system stability, performance, and robustness in complex engineering applications.
Tuning Complexity
Tuning complexity in engineering involves adjusting multiple system parameters to optimize performance, stability, and efficiency. Techniques such as model-based tuning, adaptive control, and machine learning algorithms are frequently employed to handle nonlinearities and dynamic behaviors in complex systems. The integration of real-time data analytics and automation significantly reduces manual calibration time, leading to improved accuracy and reduced operational costs. Advanced tuning methods are essential in fields like robotics, aerospace, and automotive engineering to ensure optimal functionality under varying environmental conditions.
Adaptability
Adaptability in engineering refers to the ability of systems, designs, or processes to efficiently adjust to changing requirements, environmental conditions, and technological advancements. Engineers implement adaptive mechanisms such as modular design, reconfigurable components, and scalable architectures to enhance system resilience and longevity. The integration of smart materials and adaptive control algorithms further supports real-time responsiveness and optimization in applications ranging from aerospace to civil infrastructure. This focus on adaptability ensures engineering solutions remain relevant and effective amidst evolving challenges and innovation landscapes.
Computational Demand
Engineering projects increasingly rely on advanced computational demand to solve complex problems involving simulations, data analysis, and design optimization. High-performance computing (HPC) systems and cloud-based platforms enable engineers to process large datasets and run intricate algorithms efficiently. Finite element analysis (FEA), computational fluid dynamics (CFD), and machine learning models are integral tools that drive innovation across mechanical, civil, and electrical engineering disciplines. Optimizing computational resources reduces project timelines and enhances accuracy in engineering outcomes.
Source and External Links
How Does A PID Controller Differ From A Fuzzy Logic Controller? - PID controllers use mathematical parameters and are best for simple, linear systems with predictable behavior, while fuzzy logic controllers use human-like reasoning with linguistic variables, excelling in complex, uncertain, nonlinear environments.
PID and Fuzzy Logic - NI - National Instruments - PID control relies on feedback with proportional, integral, and derivative actions ideal for physical process control, whereas fuzzy logic uses rule-based decision making allowing partial set membership, suitable for subjective and linguistic process descriptions.
PID with Fuzzy Logic Adaptive Control--The Best of Both Worlds - Fuzzy logic handles imprecision and nonlinearity, and when combined with PID tuning, it can improve control performance by adaptively optimizing PID parameters in complex processes.
FAQs
What is PID control?
PID control is a feedback control method using proportional, integral, and derivative terms to maintain a desired setpoint by minimizing the error between the setpoint and system output.
What is fuzzy logic control?
Fuzzy logic control is a control methodology that uses fuzzy set theory to handle uncertain or imprecise information by applying linguistic variables and approximate reasoning to model complex systems.
How does PID control work?
PID control works by continuously calculating an error value as the difference between a desired setpoint and a measured process variable, then applying corrective control based on proportional, integral, and derivative terms to minimize this error and achieve stable system performance.
How does fuzzy logic control work?
Fuzzy logic control works by processing input variables through fuzzification, applying a set of linguistic rules in the inference engine, and defuzzifying the output to generate precise control signals.
What are the advantages of PID control?
PID control offers advantages including precise setpoint tracking, robust disturbance rejection, simplicity of implementation, and wide applicability across various industrial processes.
What are the advantages of fuzzy logic control?
Fuzzy logic control offers advantages such as handling uncertainty and imprecision, robustness to noisy inputs, ease of incorporating expert knowledge, adaptability to nonlinear systems, and improved performance in complex, dynamic environments.
When should you use fuzzy logic instead of PID control?
Use fuzzy logic instead of PID control when the system has nonlinearities, uncertain or imprecise parameters, or when a model-based approach is impractical and expert human knowledge can guide control decisions.
 calledges.com
calledges.com