Helmholtz Resonators excel at attenuating low-frequency noise by utilizing a mass-spring system formed by an enclosed cavity and neck, making them ideal for targeted sound absorption. Quarter Wave Resonators are designed to absorb specific frequencies through resonant tube lengths that correspond to a quarter wavelength of the target sound, offering precise frequency tuning. Explore the detailed mechanisms and applications to understand which resonator suits your acoustic needs best.
Main Difference
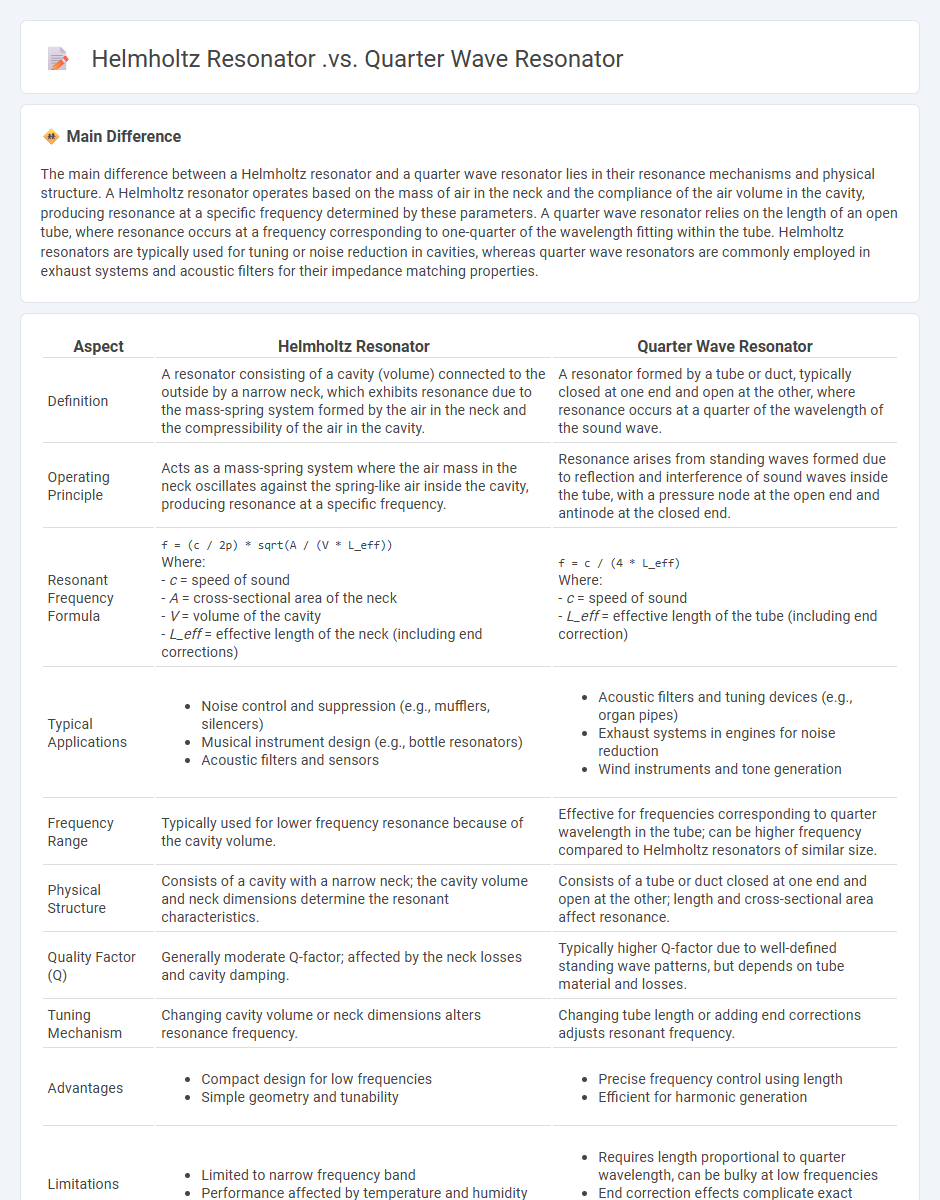
The main difference between a Helmholtz resonator and a quarter wave resonator lies in their resonance mechanisms and physical structure. A Helmholtz resonator operates based on the mass of air in the neck and the compliance of the air volume in the cavity, producing resonance at a specific frequency determined by these parameters. A quarter wave resonator relies on the length of an open tube, where resonance occurs at a frequency corresponding to one-quarter of the wavelength fitting within the tube. Helmholtz resonators are typically used for tuning or noise reduction in cavities, whereas quarter wave resonators are commonly employed in exhaust systems and acoustic filters for their impedance matching properties.
Connection
Helmholtz resonators and quarter wave resonators are both acoustic devices designed to absorb or manipulate specific frequencies of sound waves through resonance phenomena. A Helmholtz resonator operates based on the mass of air in its neck and the compliance of the air in its cavity, creating a resonance at a particular frequency, while a quarter wave resonator uses the length of a tube or cavity approximately one-quarter of the wavelength of the target frequency to produce standing waves that cancel or amplify sound. Both resonators find applications in noise control, musical acoustics, and vibration damping by attenuating unwanted frequencies through their distinct resonant properties.
Comparison Table
| Aspect | Helmholtz Resonator | Quarter Wave Resonator |
|---|---|---|
| Definition | A resonator consisting of a cavity (volume) connected to the outside by a narrow neck, which exhibits resonance due to the mass-spring system formed by the air in the neck and the compressibility of the air in the cavity. | A resonator formed by a tube or duct, typically closed at one end and open at the other, where resonance occurs at a quarter of the wavelength of the sound wave. |
| Operating Principle | Acts as a mass-spring system where the air mass in the neck oscillates against the spring-like air inside the cavity, producing resonance at a specific frequency. | Resonance arises from standing waves formed due to reflection and interference of sound waves inside the tube, with a pressure node at the open end and antinode at the closed end. |
| Resonant Frequency Formula |
f = (c / 2p) * sqrt(A / (V * L_eff))Where: - c = speed of sound - A = cross-sectional area of the neck - V = volume of the cavity - L_eff = effective length of the neck (including end corrections) |
f = c / (4 * L_eff)Where: - c = speed of sound - L_eff = effective length of the tube (including end correction) |
| Typical Applications |
|
|
| Frequency Range | Typically used for lower frequency resonance because of the cavity volume. | Effective for frequencies corresponding to quarter wavelength in the tube; can be higher frequency compared to Helmholtz resonators of similar size. |
| Physical Structure | Consists of a cavity with a narrow neck; the cavity volume and neck dimensions determine the resonant characteristics. | Consists of a tube or duct closed at one end and open at the other; length and cross-sectional area affect resonance. |
| Quality Factor (Q) | Generally moderate Q-factor; affected by the neck losses and cavity damping. | Typically higher Q-factor due to well-defined standing wave patterns, but depends on tube material and losses. |
| Tuning Mechanism | Changing cavity volume or neck dimensions alters resonance frequency. | Changing tube length or adding end corrections adjusts resonant frequency. |
| Advantages |
|
|
| Limitations |
|
|
Resonant Frequency
Resonant frequency is the specific frequency at which a system oscillates with maximum amplitude due to the natural vibration modes of its components. In engineering, this concept is critical in designing structures, mechanical systems, and electronic circuits to avoid resonance-induced failures. Materials and geometric properties of components primarily determine the resonant frequency, influencing the system's stability and performance under dynamic loads. Accurate calculation and control of resonant frequency improve safety, efficiency, and longevity in applications like bridges, automotive suspensions, and RF circuits.
Geometric Structure
Geometric structure in engineering involves the design, analysis, and optimization of shapes and forms to ensure stability, strength, and functionality of constructed systems. It plays a critical role in civil, mechanical, and aerospace engineering by determining load distribution, stress points, and material efficiency. Advanced geometric modeling techniques, including CAD (Computer-Aided Design) software and finite element analysis (FEA), enable precise simulation and improvement of structural performance. Engineering standards such as Eurocode and AISC provide guidelines for safe and efficient geometric structural design.
Damping Mechanism
A damping mechanism in engineering reduces vibrations by dissipating kinetic energy, enhancing system stability and longevity. Common types include viscous, Coulomb, and hysteretic damping, each suited for specific applications such as automotive suspensions or building structures. Materials like rubber, viscoelastic polymers, and hydraulic fluids are frequently used to achieve effective damping. Proper damping design minimizes resonance effects and improves performance in mechanical and structural engineering systems.
Frequency Range
Frequency range in engineering refers to the span of electromagnetic or signal frequencies over which a system or device operates effectively. Common frequency ranges include audio frequencies from 20 Hz to 20 kHz, radio frequencies from 3 kHz to 300 GHz, and microwave frequencies typically between 300 MHz and 300 GHz. Accurate characterization of frequency range is crucial for designing antennas, filters, and communication systems to ensure optimal performance and minimal signal distortion. Engineers utilize spectrum analyzers and network analyzers to measure and validate frequency range specifications during development and testing phases.
Acoustic Applications
Acoustic applications in engineering focus on the design and analysis of sound and vibration control systems across various industries such as automotive, aerospace, and construction. Engineers utilize advanced materials like acoustic foams and metamaterials to enhance noise reduction and improve sound quality in environments ranging from concert halls to manufacturing plants. Computational methods, including finite element analysis (FEA) and boundary element methods (BEM), enable precise modeling of acoustic wave propagation for optimized system performance. Innovations in active noise control and acoustic sensors play a critical role in improving product reliability and user comfort.
Source and External Links
Helmholtz resonance - Wikipedia - The Helmholtz resonator consists of a cavity and a neck, where air vibration in the neck acts like a mass on a spring system, producing a sharp resonant frequency based on cavity and neck geometry, commonly used for tuning and sound absorption.
Stabilization Of Self-Sustained Acoustic Oscillation Using Helmholtz And Quarter-Wave Resonators - The comparison shows that the Helmholtz resonator experiences resonance frequency drift with airflow (mass flow), while the Quarter Wave resonator is less prone to detuning and provides stable resonance under flow conditions.
Helmholtz resonators and Quarter-wave resonators are ... - Comsol - Helmholtz resonators provide higher damping capacity than Quarter Wave resonators, and using multiple resonators of either type can broaden the effective frequency range for noise reduction; background flow also affects their acoustic performance.
FAQs
What is a Helmholtz resonator?
A Helmholtz resonator is an acoustic device consisting of a cavity connected to the outside air through a narrow neck, designed to resonate at a specific frequency determined by the cavity volume, neck length, and neck diameter.
What is a quarter wave resonator?
A quarter wave resonator is a transmission line or cavity resonator designed to resonate at a fundamental frequency where its physical length equals one-quarter of the signal wavelength.
How do Helmholtz and quarter wave resonators differ in design?
Helmholtz resonators consist of a cavity connected to the outside by a narrow neck, designed to resonate at a specific frequency based on cavity volume and neck dimensions, while quarter wave resonators are tubular structures open at one end and closed at the other, resonating at a frequency determined by the tube length being one-quarter of the sound wavelength.
What are the main uses of a Helmholtz resonator?
A Helmholtz resonator is primarily used to control and reduce unwanted acoustic noise, enhance sound quality in musical instruments, and measure acoustic properties such as air volume and sound speed.
Where are quarter wave resonators commonly applied?
Quarter wave resonators are commonly applied in radio frequency (RF) circuits, including filters, antennas, and microwave devices, for impedance matching and signal filtering.
How do both resonators attenuate sound or noise?
Both Helmholtz and quarter-wave resonators attenuate sound by creating destructive interference at specific frequencies, absorbing acoustic energy and reducing noise through resonance-induced pressure variations.
Which resonator is more effective for low frequency noise control?
Helmholtz resonators are more effective for low frequency noise control due to their ability to target specific low-frequency sound waves.
 calledges.com
calledges.com