Reversible processes occur when a system changes state in such a way that both the system and surroundings can be restored to their initial conditions without any net change, making them idealized and highly efficient in thermodynamics. Irreversible processes involve energy dissipation through factors like friction, unrestrained expansion, or heat transfer with finite temperature differences, leading to increased entropy and net loss of usable energy. Explore more in-depth comparisons and practical implications of reversible versus irreversible processes in thermodynamic systems.
Main Difference
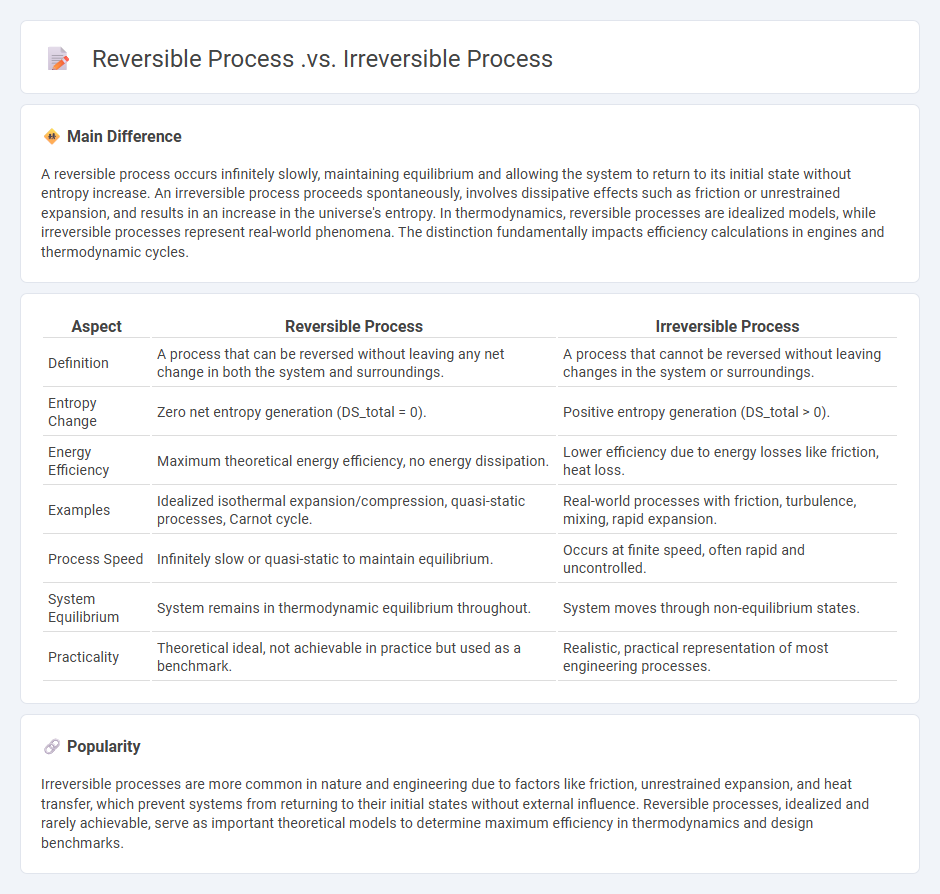
A reversible process occurs infinitely slowly, maintaining equilibrium and allowing the system to return to its initial state without entropy increase. An irreversible process proceeds spontaneously, involves dissipative effects such as friction or unrestrained expansion, and results in an increase in the universe's entropy. In thermodynamics, reversible processes are idealized models, while irreversible processes represent real-world phenomena. The distinction fundamentally impacts efficiency calculations in engines and thermodynamic cycles.
Connection
Reversible and irreversible processes are connected through the concept of entropy change in thermodynamics, where reversible processes occur without increasing the total entropy of the system and surroundings, indicating ideal, equilibrium states. Irreversible processes involve entropy generation due to factors like friction, unrestrained expansion, or heat transfer across finite temperature differences, reflecting real-world, non-equilibrium conditions. The analysis of these processes helps in understanding energy efficiency and the second law of thermodynamics.
Comparison Table
| Aspect | Reversible Process | Irreversible Process |
|---|---|---|
| Definition | A process that can be reversed without leaving any net change in both the system and surroundings. | A process that cannot be reversed without leaving changes in the system or surroundings. |
| Entropy Change | Zero net entropy generation (DS_total = 0). | Positive entropy generation (DS_total > 0). |
| Energy Efficiency | Maximum theoretical energy efficiency, no energy dissipation. | Lower efficiency due to energy losses like friction, heat loss. |
| Examples | Idealized isothermal expansion/compression, quasi-static processes, Carnot cycle. | Real-world processes with friction, turbulence, mixing, rapid expansion. |
| Process Speed | Infinitely slow or quasi-static to maintain equilibrium. | Occurs at finite speed, often rapid and uncontrolled. |
| System Equilibrium | System remains in thermodynamic equilibrium throughout. | System moves through non-equilibrium states. |
| Practicality | Theoretical ideal, not achievable in practice but used as a benchmark. | Realistic, practical representation of most engineering processes. |
Thermodynamic Equilibrium
Thermodynamic equilibrium in engineering refers to a state where all macroscopic flows of matter and energy have ceased, and the system's properties like temperature, pressure, and chemical potential are uniform throughout. This condition ensures no net change occurs within the system over time, enabling precise analysis of energy conversion processes. Engineers apply thermodynamic equilibrium concepts in designing engines, turbines, and refrigeration systems to optimize efficiency and predict system behavior under steady-state conditions. Key parameters include entropy, enthalpy, and Gibbs free energy, which dictate phase equilibria and chemical reactions in industrial applications.
Entropy Change
Entropy change in engineering quantifies the degree of disorder or randomness within a system during thermodynamic processes, fundamentally influencing energy efficiency and system performance. It is measured in joules per kelvin (J/K) and calculated using the formula DS = Q_rev/T for reversible processes, where Q_rev is the reversible heat exchange and T is the absolute temperature. Engineers analyze entropy change to optimize heat engines, refrigerators, and power plants, aiming to minimize energy losses and enhance sustainability. Accurate entropy assessments guide the design of thermodynamic cycles such as the Carnot, Rankine, and Brayton cycles, ensuring maximum work output and reduced environmental impact.
Energy Efficiency
Energy efficiency in engineering focuses on optimizing systems and processes to minimize energy consumption while maintaining desired output levels. Advanced technologies such as variable frequency drives, high-performance insulation materials, and energy recovery systems contribute significantly to reducing overall energy usage in industrial and commercial applications. The integration of smart sensors and IoT devices enables real-time monitoring and adaptive control, further enhancing energy efficiency. Sustainable engineering practices aim to lower carbon footprints and operational costs by maximizing energy utilization and minimizing waste.
Work Output
Engineering work output measures the effective energy transferred or converted by a machine or system, typically expressed in joules or watts. It reflects the useful mechanical or electrical energy generated after accounting for losses due to friction, heat, or inefficiencies. Accurate calculation of work output is essential for optimizing machine performance, improving energy efficiency, and reducing operational costs in manufacturing or industrial processes. Measuring tools like dynamometers and power meters provide precise data critical for these evaluations.
Real-World Applications
Engineering drives innovation across various industries by applying principles of physics, mathematics, and material science to solve real-world problems. Civil engineering designs and constructs infrastructure such as bridges, highways, and water systems to enhance urban development and public safety. Mechanical engineering focuses on creating efficient machinery and automotive systems, improving energy consumption and performance. Electrical engineering powers advancements in telecommunications, electronics, and renewable energy technologies, enabling sustainable and connected communities.
Source and External Links
4.2: Reversible and Irreversible Processes - Physics LibreTexts - A reversible process can restore both the system and its environment to their original states, while an irreversible process permanently alters the environment and cannot return everything to the initial condition.
Reversible and irreversible processes - Thermodynamics I - Fiveable - Reversible processes are ideal, infinitely slow, and maintain perfect equilibrium; irreversible processes occur naturally, proceed at finite rates, and are always out of equilibrium.
Reversible and Irreversible Thermodynamic Processes - YouTube - Tangerine Education - Reversible processes can theoretically be reversed with no change to the universe, while irreversible processes increase the total entropy and cannot be undone without leaving a trace.
FAQs
What is a reversible process?
A reversible process is a thermodynamic process that can be reversed without leaving any net change in the system and surroundings.
What is an irreversible process?
An irreversible process is a thermodynamic change that cannot spontaneously return both the system and surroundings to their original states without net energy loss or entropy increase.
How do reversible and irreversible processes differ?
Reversible processes occur without entropy change and can return both system and surroundings to their original states; irreversible processes increase entropy and cannot restore the initial conditions.
What are examples of reversible processes in thermodynamics?
Examples of reversible processes in thermodynamics include isothermal expansion or compression of an ideal gas, quasistatic adiabatic expansion or compression, and reversible phase changes such as melting or boiling under equilibrium conditions.
What are examples of irreversible processes in daily life?
Examples of irreversible processes in daily life include burning wood, mixing cream into coffee, rusting of iron, breaking an egg, and freezing water.
Why are reversible processes considered ideal?
Reversible processes are considered ideal because they maximize energy efficiency by minimizing entropy production and allow complete recovery of work without losses.
How does entropy change in reversible and irreversible processes?
Entropy remains constant in reversible processes and increases in irreversible processes.
 calledges.com
calledges.com