The Black-Scholes Model provides a continuous-time framework for pricing European-style options using differential equations and assumes constant volatility and risk-free rates. The Binomial Option Pricing Model offers a discrete-time approach that constructs a price tree to evaluate American and European options, accommodating early exercise features. Explore the strengths and applications of both models to enhance option pricing strategies.
Main Difference
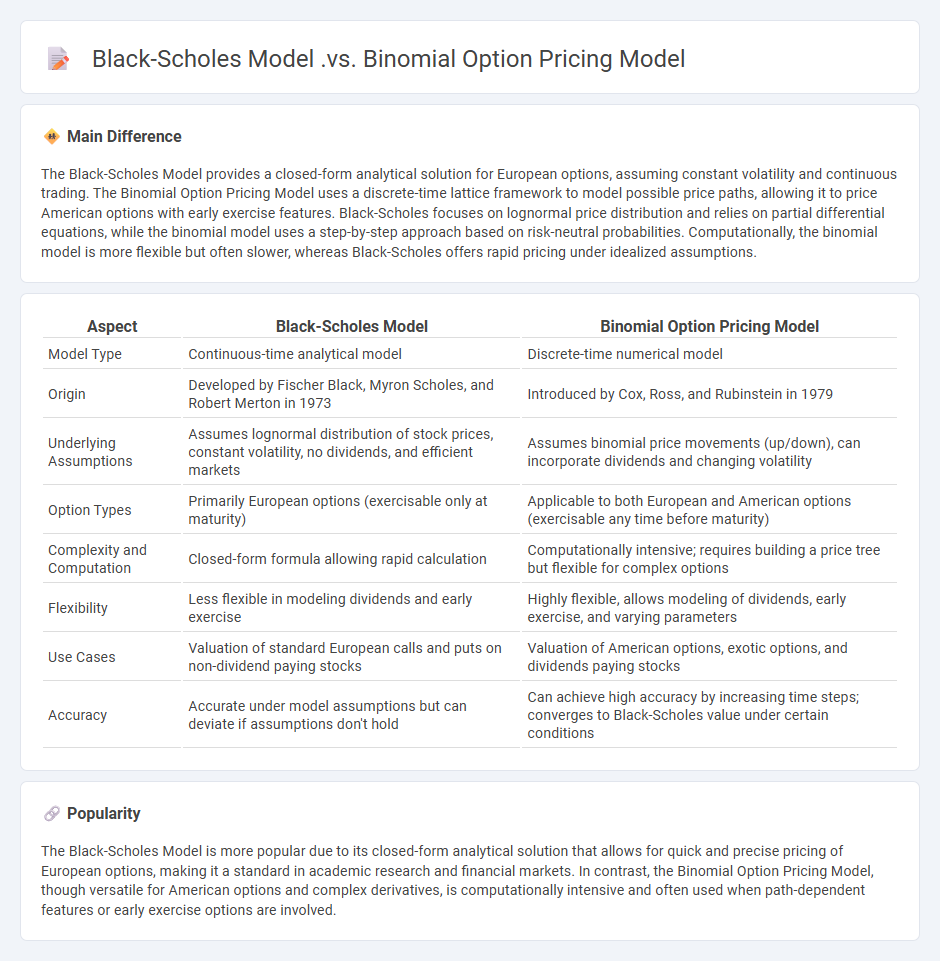
The Black-Scholes Model provides a closed-form analytical solution for European options, assuming constant volatility and continuous trading. The Binomial Option Pricing Model uses a discrete-time lattice framework to model possible price paths, allowing it to price American options with early exercise features. Black-Scholes focuses on lognormal price distribution and relies on partial differential equations, while the binomial model uses a step-by-step approach based on risk-neutral probabilities. Computationally, the binomial model is more flexible but often slower, whereas Black-Scholes offers rapid pricing under idealized assumptions.
Connection
The Black-Scholes Model and Binomial Option Pricing Model both serve to estimate the fair value of options by modeling the underlying asset's price dynamics. The Binomial Model uses a discrete-time lattice approach reflecting potential up and down price movements, while the Black-Scholes Model applies continuous-time stochastic calculus with geometric Brownian motion assumptions. As the number of binomial steps increases to infinity, the Binomial Option Pricing Model converges to the Black-Scholes Model, establishing a theoretical link between discrete and continuous valuation frameworks.
Comparison Table
| Aspect | Black-Scholes Model | Binomial Option Pricing Model |
|---|---|---|
| Model Type | Continuous-time analytical model | Discrete-time numerical model |
| Origin | Developed by Fischer Black, Myron Scholes, and Robert Merton in 1973 | Introduced by Cox, Ross, and Rubinstein in 1979 |
| Underlying Assumptions | Assumes lognormal distribution of stock prices, constant volatility, no dividends, and efficient markets | Assumes binomial price movements (up/down), can incorporate dividends and changing volatility |
| Option Types | Primarily European options (exercisable only at maturity) | Applicable to both European and American options (exercisable any time before maturity) |
| Complexity and Computation | Closed-form formula allowing rapid calculation | Computationally intensive; requires building a price tree but flexible for complex options |
| Flexibility | Less flexible in modeling dividends and early exercise | Highly flexible, allows modeling of dividends, early exercise, and varying parameters |
| Use Cases | Valuation of standard European calls and puts on non-dividend paying stocks | Valuation of American options, exotic options, and dividends paying stocks |
| Accuracy | Accurate under model assumptions but can deviate if assumptions don't hold | Can achieve high accuracy by increasing time steps; converges to Black-Scholes value under certain conditions |
Option Pricing
Option pricing involves determining the fair value of options using mathematical models such as the Black-Scholes model and the Binomial model. These models assess variables including the underlying asset price, strike price, time to expiration, volatility, interest rates, and dividends. Implied volatility, derived from market prices of options, plays a critical role in reflecting market expectations of future price fluctuations. Accurate option pricing assists traders and investors in risk management, hedging strategies, and speculative decision-making within financial markets.
Stochastic Processes
Stochastic processes in finance model the random behavior of asset prices, interest rates, and market risks over time, facilitating quantitative analysis and risk management. Popular models include the Geometric Brownian Motion for stock prices and the Cox-Ingersoll-Ross process for interest rates, which capture continuous-time stochastic dynamics. These processes underpin option pricing frameworks such as the Black-Scholes-Merton model, enabling more accurate valuation and hedging strategies. Understanding stochastic calculus and martingale theory is essential for implementing these models in practical financial applications.
Risk-Neutral Valuation
Risk-neutral valuation is a fundamental concept in financial mathematics used to price derivatives by adjusting the probability measure so that all investors are indifferent to risk. It transforms the real-world probability into a risk-neutral measure, allowing the expected discounted payoff of an asset to represent its fair value. This approach simplifies option pricing models, such as the Black-Scholes model, by removing risk premiums and focusing on the risk-free rate. The concept is essential for valuing securities in incomplete markets and is widely applied in calculating the price of options, futures, and other contingent claims.
Volatility Assumption
The volatility assumption in finance refers to the expectation regarding the degree of variation or fluctuation in the price of a financial asset over a specific period. It plays a crucial role in option pricing models such as the Black-Scholes model, where implied volatility is used to estimate future market uncertainty. Volatility is commonly measured using statistical metrics like standard deviation or variance of returns, and it affects risk assessment, portfolio management, and derivative pricing. Accurate volatility assumptions enhance forecasting accuracy and inform strategic investment decisions.
Discrete vs Continuous Models
Discrete models in finance analyze asset prices at specific time intervals, employing tools like binomial trees and difference equations to forecast market behaviors. Continuous models, such as the Black-Scholes framework, utilize stochastic differential equations to represent price evolution in uninterrupted time, capturing more dynamic market fluctuations. Quantitative analysts often prefer continuous models for derivative pricing due to their mathematical tractability and ability to model complex instruments. Empirical studies reveal that combining discrete and continuous approaches enhances risk management and option valuation accuracy.
Source and External Links
### Resources for ComparisonBinomial Option Pricing Model Explained - This webpage explains the binomial option pricing model, highlighting its simplicity and applications, including pricing American options.
Option Pricing Models (Black-Scholes & Binomial) - This resource compares the Black-Scholes and binomial models, noting that the binomial model provides a computational approach to solving option pricing problems.
Comparison: Binomial model and Black Scholes model - This article compares the simplicity of the binomial model with the complexity of the Black-Scholes model, which requires solving a stochastic differential equation.
FAQs
What is the Black-Scholes model?
The Black-Scholes model is a mathematical formula used to calculate the theoretical price of European-style options by modeling the dynamics of the underlying asset's price with geometric Brownian motion and assuming a constant volatility and risk-free interest rate.
What is the Binomial Option Pricing model?
The Binomial Option Pricing model is a discrete-time method for valuing options by simulating possible price paths of the underlying asset through a binomial tree, calculating option values at each node using risk-neutral probabilities.
How do the Black-Scholes and Binomial models differ in approach?
The Black-Scholes model uses continuous-time stochastic calculus with a closed-form formula assuming constant volatility and risk-free rate, while the Binomial model employs a discrete-time lattice framework to approximate option prices through multiple possible price paths and can handle varying conditions and American options.
What are the main assumptions of the Black-Scholes model?
The Black-Scholes model assumes lognormal asset price distribution, constant volatility, constant risk-free interest rate, no dividends, frictionless markets without arbitrage opportunities, continuous trading, and European-style options exercisable only at maturity.
What are the main advantages of the Binomial model?
The Binomial model offers advantages such as flexibility in modeling various option types, ability to handle American options with early exercise features, and convergence to the Black-Scholes model as the number of time steps increases.
Which model is better for American options?
The Binomial options pricing model is better for American options due to its flexibility in handling early exercise features.
How does volatility affect the pricing outcome in each model?
In the Black-Scholes model, higher volatility increases option prices by raising expected payoff variability; in the Binomial model, greater volatility expands the range of possible price outcomes, leading to higher option values.
 calledges.com
calledges.com