The Gauss-Markov Theorem establishes conditions under which the Ordinary Least Squares (OLS) estimator is the Best Linear Unbiased Estimator (BLUE) in linear regression models, assuming errors are uncorrelated and homoscedastic. Martingale Theory, rooted in stochastic processes, focuses on fair game dynamics where future conditional expectations equal current values, extensively applied in financial mathematics and time series analysis. Explore the fundamental distinctions and applications of these concepts to deepen your understanding of statistical inference and probabilistic modeling.
Main Difference
The Gauss-Markov Theorem states that in a linear regression model with homoscedastic, uncorrelated errors, the ordinary least squares (OLS) estimator is the best linear unbiased estimator (BLUE). Martingale Theory, rooted in probability and stochastic processes, describes a sequence of random variables where the conditional expectation of the next value, given past values, equals the current value, emphasizing the concept of "fair game" in time series analysis. Gauss-Markov focuses on estimator efficiency in linear models, while Martingale Theory addresses the evolution and prediction in stochastic processes. Both theories underpin different areas of statistical inference and probability modeling.
Connection
The Gauss-Markov Theorem guarantees that the Ordinary Least Squares (OLS) estimator is the Best Linear Unbiased Estimator (BLUE) under the assumptions of linear regression with homoscedastic and uncorrelated errors. Martingale theory provides a probabilistic framework that generalizes the concept of uncorrelatedness by modeling error terms as martingale difference sequences, ensuring zero conditional mean and orthogonality conditions required for unbiasedness. This connection allows the extension of the Gauss-Markov results to more complex dependent structures beyond simple i.i.d. errors, enhancing the robustness and applicability of linear estimators in time series and stochastic process contexts.
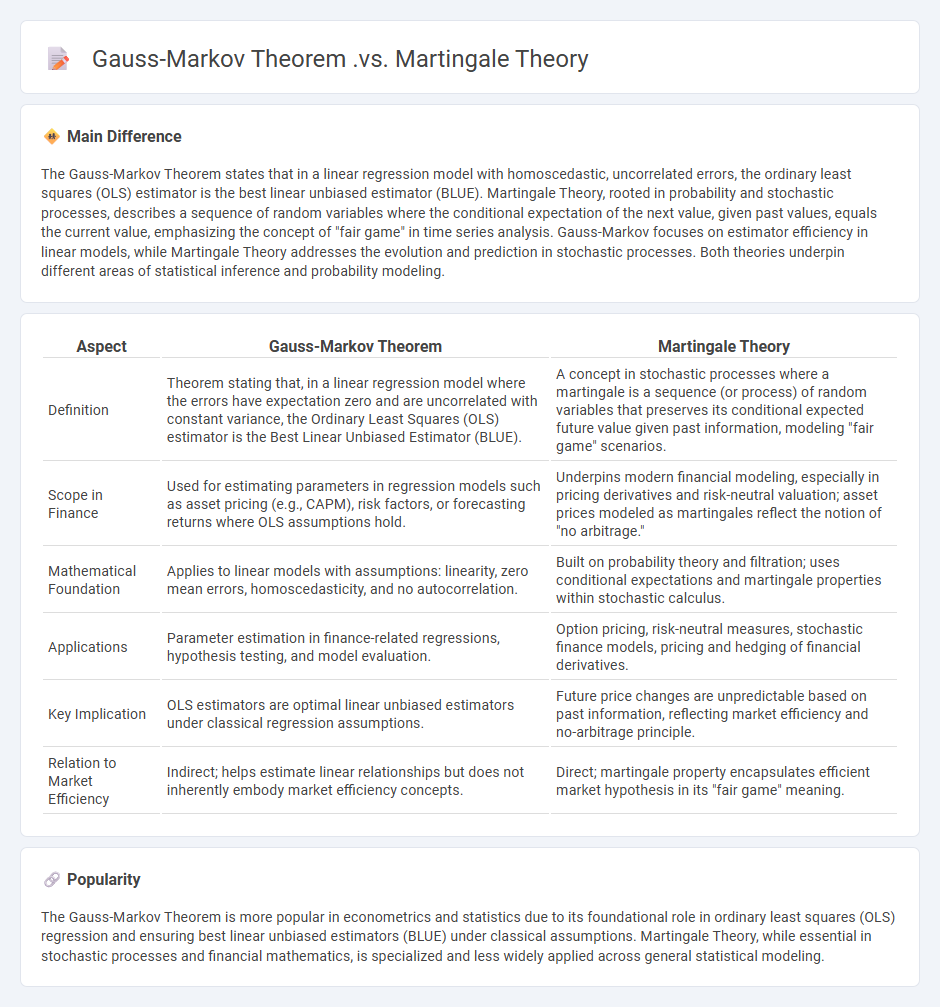
Comparison Table
| Aspect | Gauss-Markov Theorem | Martingale Theory |
|---|---|---|
| Definition | Theorem stating that, in a linear regression model where the errors have expectation zero and are uncorrelated with constant variance, the Ordinary Least Squares (OLS) estimator is the Best Linear Unbiased Estimator (BLUE). | A concept in stochastic processes where a martingale is a sequence (or process) of random variables that preserves its conditional expected future value given past information, modeling "fair game" scenarios. |
| Scope in Finance | Used for estimating parameters in regression models such as asset pricing (e.g., CAPM), risk factors, or forecasting returns where OLS assumptions hold. | Underpins modern financial modeling, especially in pricing derivatives and risk-neutral valuation; asset prices modeled as martingales reflect the notion of "no arbitrage." |
| Mathematical Foundation | Applies to linear models with assumptions: linearity, zero mean errors, homoscedasticity, and no autocorrelation. | Built on probability theory and filtration; uses conditional expectations and martingale properties within stochastic calculus. |
| Applications | Parameter estimation in finance-related regressions, hypothesis testing, and model evaluation. | Option pricing, risk-neutral measures, stochastic finance models, pricing and hedging of financial derivatives. |
| Key Implication | OLS estimators are optimal linear unbiased estimators under classical regression assumptions. | Future price changes are unpredictable based on past information, reflecting market efficiency and no-arbitrage principle. |
| Relation to Market Efficiency | Indirect; helps estimate linear relationships but does not inherently embody market efficiency concepts. | Direct; martingale property encapsulates efficient market hypothesis in its "fair game" meaning. |
Linear Regression Assumptions
Linear regression in finance relies on key assumptions such as linearity, which ensures a straight-line relationship between independent variables like interest rates or market indices and dependent variables such as stock returns. Homoscedasticity requires constant variance of residuals, critical for accurate risk modeling and portfolio optimization. Financial datasets must also observe the independence of errors to avoid autocorrelation, which is common in time series data like asset prices. Finally, the normality of residuals supports valid hypothesis testing, essential for forecasting and valuation models.
Efficient Market Hypothesis
The Efficient Market Hypothesis (EMH) asserts that financial markets fully reflect all available information, making it impossible to consistently achieve higher returns than the overall market through stock picking or market timing. EMH is categorized into three forms: weak, semi-strong, and strong, each differing by the scope of information reflected in asset prices. Empirical research shows mixed evidence, with some anomalies like momentum and value effects challenging the hypothesis. Prominent economists such as Eugene Fama have contributed extensively to popularizing EMH in modern finance theory.
BLUE (Best Linear Unbiased Estimator)
BLUE (Best Linear Unbiased Estimator) is a statistical method used in finance to produce efficient and unbiased parameter estimates in linear regression models. It minimizes variance among all linear unbiased estimators, making it crucial for asset pricing models and risk assessment. Common applications include estimating beta coefficients in the Capital Asset Pricing Model (CAPM) and forecasting financial returns based on historical data. Accurate BLUE estimates improve portfolio optimization and financial decision-making by reducing estimation errors.
Predictability vs. Fair Game Process
Predictability in finance refers to the ability to forecast asset price movements based on historical data, economic indicators, or market trends. A fair game process implies that price changes are random and unbiased, making it impossible to consistently achieve excess returns through prediction. Empirical studies of financial markets often find asset returns follow a martingale or random walk process, supporting the fair game hypothesis. This has profound implications for strategies relying on market efficiency and challenges models assuming persistent predictability.
Time Series Modeling
Time series modeling in finance involves analyzing historical financial data, such as stock prices, interest rates, and exchange rates, to forecast future trends and inform investment decisions. Techniques like ARIMA, GARCH, and LSTM neural networks are widely used for capturing patterns and volatility in financial time series. Accurate modeling supports risk management, portfolio optimization, and algorithmic trading strategies by identifying temporal dependencies and market anomalies. Financial institutions leverage these models to enhance predictive accuracy and improve strategic planning.
Source and External Links
Gauss Markov Theorem & Assumptions - The Gauss-Markov theorem guarantees that under specific assumptions (linearity, random sampling, non-collinearity, exogeneity, and homoscedasticity), the ordinary least squares (OLS) estimator is the Best Linear Unbiased Estimator (BLUE) for regression coefficients, making it a fundamental result in regression analysis.
The fundamental martingale with applications to Markov ... - Martingale theory, notably involving sequences of random variables with specific conditional expectation properties, plays a central role in probability theory and stochastic processes, with fundamental martingales used to structure Gaussian processes and model their dependence and evolution over time.
Gauss-Markov theorem - The Gauss-Markov theorem is primarily a statistical result in econometrics ensuring that, given the assumptions, OLS estimators are the best linear unbiased estimators for modeling relationships in regression, whereas martingale theory deals with stochastic processes and their conditional expectations in probability.
FAQs
What is the Gauss-Markov Theorem?
The Gauss-Markov Theorem states that in a linear regression model where the errors have zero mean, are uncorrelated, and have equal variance (homoscedasticity), the Ordinary Least Squares (OLS) estimator is the Best Linear Unbiased Estimator (BLUE).
What is Martingale Theory in probability?
Martingale Theory in probability studies stochastic processes where the conditional expected value of the next observation, given all prior observations, equals the current observation, modeling fair game dynamics.
How do the assumptions differ between Gauss-Markov and Martingale frameworks?
Gauss-Markov assumptions require linearity, zero mean errors, homoscedasticity, no autocorrelation, and fixed regressors; Martingale frameworks assume conditional mean zero errors with respect to past information, allowing dependent structures but requiring the martingale difference property instead of independence or homoscedasticity.
What are the core uses of the Gauss-Markov Theorem?
The Gauss-Markov Theorem ensures that Ordinary Least Squares (OLS) estimators are the Best Linear Unbiased Estimators (BLUE) under the assumptions of linearity, zero mean errors, homoscedasticity, and no autocorrelation, making it essential for efficient linear regression analysis in econometrics and statistics.
How is Martingale Theory applied in real-world problems?
Martingale Theory models fair game processes in finance for option pricing, risk assessment, and algorithmic trading, and in statistics for sequential analysis and hypothesis testing.
How do both theories handle the concept of independence?
Classical probability theory defines independence as the product of probabilities of events, P(A B) = P(A)P(B), while Bayesian theory interprets independence as a lack of informational influence, where the occurrence of one event does not update the probability of another, expressed as P(A|B) = P(A).
Which fields predominantly use Gauss-Markov and Martingale Theory?
Gauss-Markov theorem is predominantly used in econometrics and statistics for linear regression analysis, while Martingale theory is extensively applied in financial mathematics, stochastic processes, and probability theory.
 calledges.com
calledges.com