The Merton Model focuses on credit risk by modeling a firm's asset value to assess default probability, while the Black-Scholes Model is used for pricing European options based on underlying asset volatility and risk-free rates. Both models apply stochastic processes but serve distinct financial applications: credit risk assessment for Merton and options pricing for Black-Scholes. Explore more to understand the practical implications and mathematical foundations of these fundamental models.
Main Difference
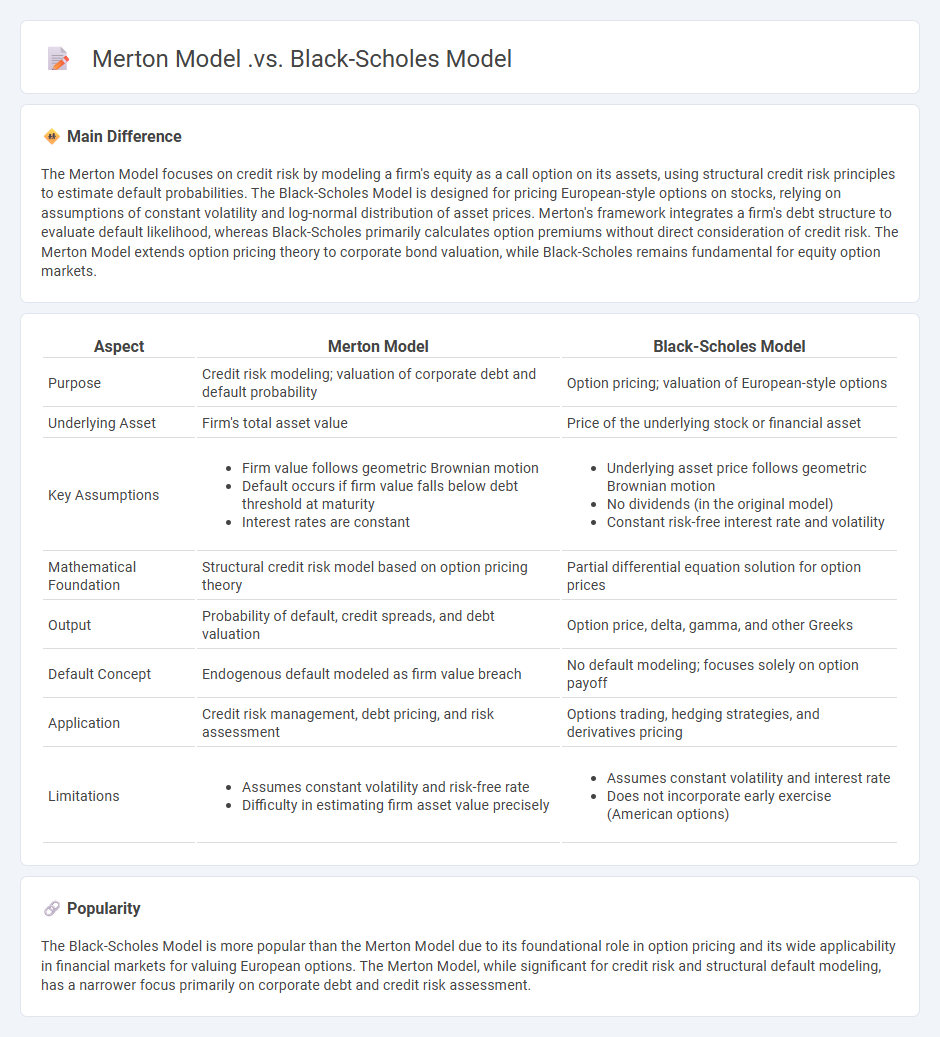
The Merton Model focuses on credit risk by modeling a firm's equity as a call option on its assets, using structural credit risk principles to estimate default probabilities. The Black-Scholes Model is designed for pricing European-style options on stocks, relying on assumptions of constant volatility and log-normal distribution of asset prices. Merton's framework integrates a firm's debt structure to evaluate default likelihood, whereas Black-Scholes primarily calculates option premiums without direct consideration of credit risk. The Merton Model extends option pricing theory to corporate bond valuation, while Black-Scholes remains fundamental for equity option markets.
Connection
The Merton Model extends the Black-Scholes Model by applying option pricing theory to corporate debt, treating a company's equity as a call option on its assets. Both models rely on stochastic processes and the assumption of log-normal asset price distribution to evaluate financial derivatives. Merton's framework integrates default risk into structural credit risk modeling, linking equity valuation directly to the firm's asset volatility and capital structure.
Comparison Table
| Aspect | Merton Model | Black-Scholes Model |
|---|---|---|
| Purpose | Credit risk modeling; valuation of corporate debt and default probability | Option pricing; valuation of European-style options |
| Underlying Asset | Firm's total asset value | Price of the underlying stock or financial asset |
| Key Assumptions |
|
|
| Mathematical Foundation | Structural credit risk model based on option pricing theory | Partial differential equation solution for option prices |
| Output | Probability of default, credit spreads, and debt valuation | Option price, delta, gamma, and other Greeks |
| Default Concept | Endogenous default modeled as firm value breach | No default modeling; focuses solely on option payoff |
| Application | Credit risk management, debt pricing, and risk assessment | Options trading, hedging strategies, and derivatives pricing |
| Limitations |
|
|
Default Risk
Default risk refers to the probability that a borrower will be unable to meet their debt obligations, leading to a failure in making scheduled interest or principal payments. This risk is a critical component in credit analysis and influences the pricing of bonds, loans, and other fixed-income securities. Credit rating agencies, such as Moody's and Standard & Poor's, assess default risk by evaluating borrowers' financial health, payment history, and economic conditions. Investors demand higher yields on securities with elevated default risk to compensate for potential losses.
Structural Credit Model
Structural credit models assess credit risk by modeling a firm's asset value dynamics to determine default probability based on the firm's capital structure. The Merton model is a foundational framework using option pricing theory to estimate the likelihood that a firm's assets fall below its debt obligations at maturity. These models employ firm-specific financial data and market variables, enabling quantification of credit spreads and default correlations in portfolio risk management. Structural models are essential in pricing corporate bonds, credit derivatives, and managing counterparty risk in financial markets.
Option Pricing
Option pricing involves the valuation of financial derivatives that grant the holder the right, but not the obligation, to buy or sell an underlying asset at a predetermined price before or at expiration. The Black-Scholes model, developed by Fischer Black and Myron Scholes in 1973, remains a foundational quantitative method for European-style option valuation, computing prices based on factors such as underlying asset price, strike price, volatility, time to expiration, risk-free interest rate, and dividends. Other models like the Binomial model provide a discrete-time framework suitable for American-style options, accounting for early exercise features. Volatility estimation, implied volatility, and Greeks like Delta and Gamma are critical for understanding option sensitivities and managing risk in option pricing.
Stochastic Processes
Stochastic processes play a crucial role in finance by modeling the random behavior of asset prices, interest rates, and market risks. The most widely used stochastic model is the Geometric Brownian Motion, fundamental to the Black-Scholes option pricing framework. Advanced techniques such as jump diffusion models and stochastic volatility models provide more accurate representations of financial markets' complexities. Understanding and applying stochastic calculus enables quantitative analysts to evaluate derivatives and manage portfolio risk effectively.
Equity Valuation
Equity valuation involves assessing a company's stock value using models like discounted cash flow (DCF), dividend discount model (DDM), and comparable company analysis (CCA). Financial analysts estimate future earnings, cash flows, and risk factors to determine intrinsic stock value relative to market price. Key metrics include price-to-earnings (P/E) ratio, price-to-book (P/B) ratio, and return on equity (ROE) to gauge investment potential. Accurate equity valuation supports informed decisions in stock trading, portfolio management, and corporate finance.
Source and External Links
Black-Scholes-Merton approach - merits and shortcomings - The Merton model is part of the Black-Scholes-Merton framework, primarily used for pricing options based on the underlying asset price, volatility, time to maturity, and risk-free rate, focusing on financial derivatives pricing, especially European options.
Black-Scholes-Merton Model | Assumptions | Calculation - Fintelligents - The Black-Scholes-Merton model prices European stock options using a differential equation based on assumptions such as continuous trading, no dividends, and constant volatility; it does not handle American options well due to their early exercise feature.
Black-Scholes model - Wikipedia - The Black-Scholes-Merton model, developed by Black, Scholes, and expanded by Merton, revolutionized option pricing by introducing the risk-neutral dynamic hedging argument, earning Merton and Scholes a Nobel Prize and underpinning modern derivatives markets.
FAQs
What is the Merton Model?
The Merton Model is a structural credit risk model that assesses a firm's default risk by modeling its equity as a call option on its assets, predicting default when asset value falls below debt obligations at maturity.
What is the Black-Scholes Model?
The Black-Scholes Model is a mathematical framework used to calculate the theoretical price of European-style options by modeling the dynamics of asset prices under assumptions of constant volatility and risk-free interest rates.
How do the Merton Model and Black-Scholes Model differ?
The Merton Model values corporate debt by modeling a firm's equity as a call option on its assets with default risk, while the Black-Scholes Model prices options assuming no default risk and uses constant volatility.
What assumptions does the Black-Scholes Model make?
The Black-Scholes Model assumes stock prices follow a geometric Brownian motion with constant volatility and drift, markets are frictionless with no transaction costs or taxes, no dividends are paid, risk-free interest rates are constant and known, trading is continuous, and there are no arbitrage opportunities.
How does the Merton Model address default risk?
The Merton Model addresses default risk by modeling a firm's equity as a European call option on its assets, with default occurring if asset value falls below debt obligations at maturity.
In which scenarios is the Merton Model preferred over Black-Scholes?
The Merton Model is preferred over Black-Scholes in credit risk analysis for valuing corporate debt and default probability estimation.
What are the main applications of both models in finance?
Risk assessment, algorithmic trading, portfolio optimization, fraud detection, and credit scoring are the main applications of machine learning and statistical models in finance.
 calledges.com
calledges.com