Value at Risk (VaR) quantifies the maximum potential loss within a specified confidence level and time horizon, serving as a fundamental risk metric in finance. Conditional Value at Risk (CVaR), also known as Expected Shortfall, measures the average loss exceeding the VaR threshold, providing deeper insight into tail risk. Explore the key differences between VaR and CVaR to enhance your risk management strategies.
Main Difference
Value at Risk (VaR) estimates the maximum potential loss over a specified time period at a given confidence level, focusing on the threshold loss without detailing the severity beyond that point. Conditional Value at Risk (CVaR), also known as Expected Shortfall, measures the average loss exceeding the VaR threshold, providing insight into tail risk and extreme losses. CVaR offers a more comprehensive risk assessment by considering the magnitude of losses in the tail of the loss distribution, making it more sensitive to extreme market events. Financial institutions often prefer CVaR for robust risk management and regulatory compliance due to its coherent risk measure properties.
Connection
Value at Risk (VaR) estimates the maximum potential loss over a specified time frame at a given confidence level, while Conditional Value at Risk (CVaR) measures the expected loss exceeding the VaR threshold. CVaR provides a more comprehensive risk assessment by considering tail-end losses beyond the VaR cutoff, addressing scenarios of extreme financial stress. Both metrics are integral to risk management, with CVaR refining VaR's limitations by capturing the severity of rare but impactful losses.
Comparison Table
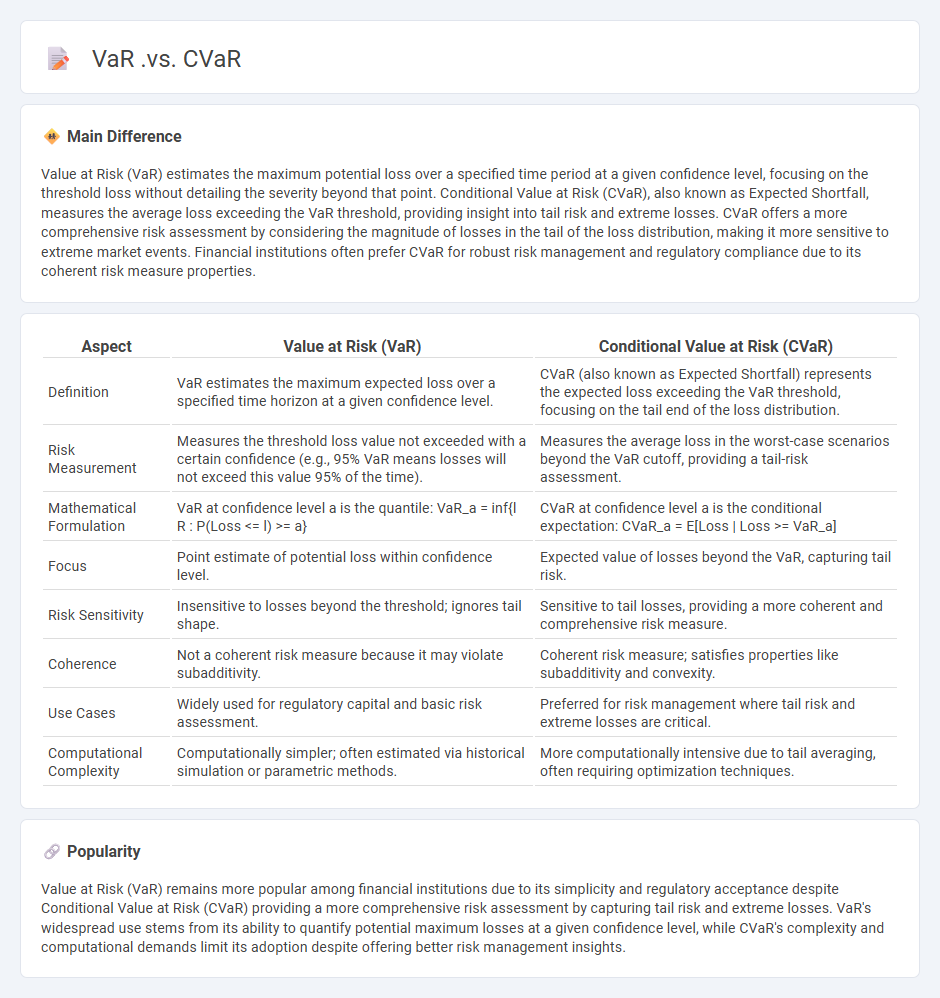
| Aspect | Value at Risk (VaR) | Conditional Value at Risk (CVaR) |
|---|---|---|
| Definition | VaR estimates the maximum expected loss over a specified time horizon at a given confidence level. | CVaR (also known as Expected Shortfall) represents the expected loss exceeding the VaR threshold, focusing on the tail end of the loss distribution. |
| Risk Measurement | Measures the threshold loss value not exceeded with a certain confidence (e.g., 95% VaR means losses will not exceed this value 95% of the time). | Measures the average loss in the worst-case scenarios beyond the VaR cutoff, providing a tail-risk assessment. |
| Mathematical Formulation | VaR at confidence level a is the quantile: VaR_a = inf{l R : P(Loss <= l) >= a} | CVaR at confidence level a is the conditional expectation: CVaR_a = E[Loss | Loss >= VaR_a] |
| Focus | Point estimate of potential loss within confidence level. | Expected value of losses beyond the VaR, capturing tail risk. |
| Risk Sensitivity | Insensitive to losses beyond the threshold; ignores tail shape. | Sensitive to tail losses, providing a more coherent and comprehensive risk measure. |
| Coherence | Not a coherent risk measure because it may violate subadditivity. | Coherent risk measure; satisfies properties like subadditivity and convexity. |
| Use Cases | Widely used for regulatory capital and basic risk assessment. | Preferred for risk management where tail risk and extreme losses are critical. |
| Computational Complexity | Computationally simpler; often estimated via historical simulation or parametric methods. | More computationally intensive due to tail averaging, often requiring optimization techniques. |
Value at Risk (VaR)
Value at Risk (VaR) quantifies the potential loss in value of a portfolio over a defined period for a given confidence interval. Financial institutions use VaR to measure market risk exposure, typically calculating daily VaR at confidence levels such as 95% or 99%. Common methods to compute VaR include Historical Simulation, Variance-Covariance, and Monte Carlo Simulation, each varying in assumptions and computational complexity. Regulators like the Basel Committee use VaR metrics to set capital requirements ensuring banks maintain sufficient reserves against market fluctuations.
Conditional Value at Risk (CVaR)
Conditional Value at Risk (CVaR) is a risk assessment measure used in finance to evaluate the expected loss exceeding the Value at Risk (VaR) threshold at a specified confidence level, commonly 95% or 99%. CVaR provides a more comprehensive risk assessment by accounting for tail-end losses beyond the VaR cutoff, making it essential for stress testing and portfolio optimization. Financial institutions use CVaR to manage extreme market risks, improve capital allocation, and satisfy regulatory requirements such as Basel III. The calculation of CVaR involves integrating the loss distribution tail, often through Monte Carlo simulation or historical data analysis.
Tail Risk
Tail risk represents the probability of extreme financial losses occurring in the far ends of a probability distribution, beyond the typical expectations of standard deviation models. This risk primarily affects investment portfolios, where rare but severe market events lead to significant negative returns, often unaccounted for by models assuming normal distribution. Financial instruments such as options and derivatives are frequently employed to hedge against these low-probability, high-impact tail events. Quantitative risk management techniques, including Value at Risk (VaR) and stress testing, aim to estimate and mitigate tail risk exposure to protect assets under extreme market conditions.
Risk Threshold
Risk threshold in finance refers to the maximum level of risk an investor or institution is willing to accept when making investment decisions or managing portfolios. It is determined based on factors such as investment objectives, time horizon, and financial capacity. Setting a risk threshold helps in mitigating potential losses by aligning the portfolio strategy with risk tolerance levels. Financial tools like Value at Risk (VaR) and stress testing are commonly used to quantify and manage risk thresholds.
Probability Distribution
Probability distribution in finance quantifies the likelihood of different outcomes for asset returns, helping investors assess risk and expected performance. Common distributions include normal, log-normal, and binomial, which model stock prices, option pricing, and credit risk. Financial models like the Black-Scholes option pricing model rely on probability distributions to forecast derivative prices under market uncertainty. Understanding these distributions supports portfolio optimization, risk management, and strategic decision-making in markets.
Source and External Links
Extensions of VaR - CFA, FRM, and Actuarial Exams Study - CVaR (Conditional VaR) measures the expected losses beyond the VaR cutoff point at a specific confidence level, quantifying tail risks, whereas VaR itself identifies a loss threshold not exceeded with a certain confidence; also, Marginal VaR and Incremental VaR differ by how they assess changes in portfolio risk.
Expected Shortfall (or Conditional VaR or CVar) - CVaR is the average of losses beyond the VaR threshold, representing the expected loss in the worst (1-p)% scenarios, making it a more conservative risk measure than VaR which only sets a cutoff point.
Value at Risk VAR and CVaR - VaR offers an easy-to-understand single number summarizing risk up to a confidence level, while CVaR or Expected Shortfall assesses the average loss in the tail beyond the VaR level, providing a coherent and more conservative measure favored in financial risk management.
FAQs
What is Value at Risk?
Value at Risk (VaR) is a statistical measure that estimates the maximum potential loss of a portfolio or asset over a specified time period at a given confidence level.
What is Conditional Value at Risk?
Conditional Value at Risk (CVaR) measures the expected loss exceeding a specified Value at Risk (VaR) threshold, quantifying potential extreme losses in financial risk management.
How do VaR and CVaR differ?
VaR measures the maximum potential loss at a specific confidence level, while CVaR calculates the average loss exceeding the VaR threshold, providing a risk assessment of tail-end losses.
How is VaR calculated?
Value at Risk (VaR) is calculated by determining the maximum potential loss over a specified time horizon at a given confidence level using methods like historical simulation, variance-covariance, or Monte Carlo simulation.
How is CVaR calculated?
CVaR (Conditional Value at Risk) is calculated as the expected loss exceeding the Value at Risk (VaR) at a given confidence level, defined by the formula: CVaR_a = E[L | L > VaR_a], where L represents losses and a is the confidence level.
What are the uses of VaR and CVaR in risk management?
VaR quantifies potential maximum loss at a given confidence level, aiding in risk limit setting and regulatory capital calculation. CVaR measures the expected loss beyond VaR, improving assessment of tail risk and informing stress testing and portfolio optimization.
What are the limitations of VaR and CVaR?
VaR limitations include lack of subadditivity, inability to capture tail risk beyond the threshold, and sensitivity to model assumptions. CVaR limitations involve computational complexity, reliance on accurate tail distribution estimation, and potential sensitivity to extreme outliers.
 calledges.com
calledges.com